Оценивание параметров законов распределения

Рассмотрим задачу оценивания r параметров 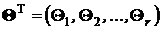закона распределения (плотности распределения) 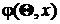случайной величины x по выборочным данным.

Поскольку

,

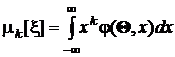все начальные моменты являются функциями искомых параметров, и в общем случае можно записать

.

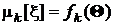Точно так же функциями параметров являются и центральные моменты. В качестве примеров таких функций можно привести экспоненциальный и равномерный законы распределения, для которых, как было установлено в разд. 1.6.6:

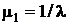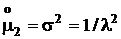, – для экспоненциального закона;

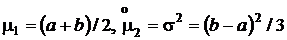– для равномерного закона.

Указанные зависимости используются для оценивания параметров Θ в тех случаях, когда закон распределения генеральной совокупности известен. С этой целью по выборочным данным находят оценки моментов. Количество моментов, подлежащих определению, должно быть равно числу rискомых параметров. Таким образом будут получено rуравнений:

.

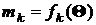Искомые параметры находят путем решения этих уравнений.

Свойства точечных оценок

Поскольку выборочные значения (вектор выборочных значений) случайны на множестве исходов экспериментов, повторяющихся в неизменных условиях и в неизменном объеме, то оценки моментов и параметров законов распределения также случайны, а потому в качестве характеристик их свойств применяют вероятностные критерии.

Применим общее обозначение генеральных моментов и параметров случайных величин и их законов распределения: Q. Для обозначения оценок моментов и параметров, вычисляемых по выборке объема n, будем использовать обозначение .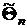

Важнейшими свойствами точечных оценок являются: несмещенность, эффективность, состоятельность. В последнее время возрастает роль четвертого свойства – устойчивости (resistance).

a) Оценка момента (или параметра) является несмещенной, если ее математическое ожидание при фиксированном объеме выборки n равно оцениваемому генеральному моменту или параметру:

.

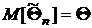б) Оценка момента (или параметра) эффективна, если при фиксированном объеме выборки n она обладает минимальной дисперсией среди всех оценок данного момента (параметра):

.

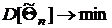в) Оценка момента (или параметра) состоятельна, если с увеличением объема выборки nона стремится по вероятности к генеральному значению момента (или параметра), то есть если при любом сколько угодно малом положительном e

.

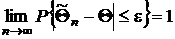г) Устойчивые оценки – оценки, нечувствительные или малочувствительные к возмущениям в виде грубых промахов измерений, погрешностям вычислений и т.п.

Оценки могут быть:

несмещенные, эффективные, состоятельные;

несмещенные, но неэффективные;

эффективные, но смещенные;

смещенные при каждом фиксированном n , но состоятельные, такие оценки являются асимптотически несмещенными.

2.3.4.1. Свойства оценок математического ожидания

Выборка 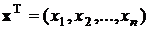извлечена из генеральной совокупности X, образованной случайной величиной x. Генеральные моменты: математическое ожидание M[x]= 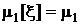, дисперсия .

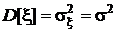Для оценки математического ожидания используют несколько видов оценок. Наиболее популярной оценкой является среднее арифметическое значение

.

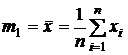Среди других оценок назовем выборочную медиану 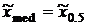и середину размаха 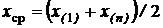, которые применяются в случаях, когда случайная величина xимеет симметричную плотность распределения.

Рассмотрим подробно свойства оценки .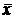

a) П р о в е р и м н е с м е щ е н н о с т ь среднего арифметического, используя формулы для математического ожидания линейной функции от случайной величины, полученные в разд. 1.6.5:

,

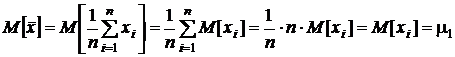а это означает, что среднее арифметическое выборочных значений есть несмещенная оценка математического ожидания случайной величины независимо от вида закона распределения.

б) Н а й д е м д и с п е р с и ю среднего арифметического, используя те же формулы разд. 1.6.5 с учетом следующих обстоятельств:

выборочные значения попарно независимы;

выборочные значения случайны на множестве групп экспериментов объемом n, и каждое из них распределено так же, как случайная величина x, каждое выборочное значениеимеет числовые характеристики генеральной совокупности.

.

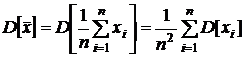Поскольку выборочные значения 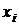изъяты из одной генеральной совокупности, их дисперсии одинаковы. Поэтому

.

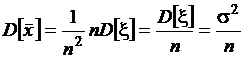Среднеквадратическое значение среднего арифметического

.

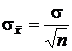Из полученных соотношений видно, что обработка результатов многократных измерений путем вычисления среднего арифметического небесполезна, ибо показатель разброса значений средних арифметических убывает с увеличением объема выборки.

Из последующего материала (разд. 2.3.5) мы узнаем:

что среднее арифметическое – эффективная оценка математического ожидания нормальной случайной величин;

что выборочная медиана – несмещенная оценка математического ожидания случайных величин с симметричной плотностью распределения, она является эффективной оценкой математического ожидания случайной величины, распределенной по Лапласу (см. также разд. 2.3.5);

что середина размаха – несмещенная оценка математического ожидания случайных величин с симметричной плотностью распределения и является эффективной оценкой математического ожидания случайной величины, распределенной равномерно или по закону Arcsin.

в) П р о в е р и м с о с т о я т е л ь н о с т ь среднего арифметического, как оценки математического ожидания.

Применим неравенство Чебышева (разд. 1.6.8), приняв в качестве случайной величины xсреднее арифметическое 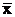с дисперсией 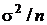. Из неравенства

следует противоположное ему:

.

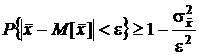Поскольку среднее арифметическое есть несмещенная оценка математического ожидания, 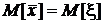. Поэтому

.

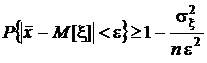Каким бы малым не было e, его значение фиксировано, поэтому при n ® ¥ вычитаемое в правой части неравенства стремится к нулю, а правая часть – к единице.

Таким образом, состоятельность среднего арифметического как оценки математического ожидания доказана независимо от вида закона распределения.

Мы получили пример полезного применения неравенства Чебышева, несмотря на грубость даваемой им оценки.

Выборочная медиана и середина размаха – состоятельные оценки математического ожидания случайных величин с симметричной плотностью распределения.

г) П л о т н о с т ь р а с п р е д е л е н и я среднего арифметического.

Примем вначале, что выборка извлечена из нормальной генеральной совокупности 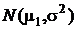. Тогда на множестве групп экспериментов каждое выборочное значение распределено также нормально, то есть 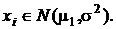В силу безграничной делимости нормального распределения сумма выборочных значений распределена нормально, а умножение ее на множитель 1/n приводит лишь к изменению масштаба. Таким образом, на основании свойств a) и b) получаем, что

.

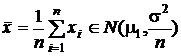Более того, по центральной предельной теореме (разд. 1.6.6.4), плотность распределения среднего арифметического ассимптотически нормальна вне зависимости от вида плотности распределения генеральных совокупностей, из которых изъяты выборочные значения.

2.3.4.2. Свойства оценок дисперсии

a) Рассмотрим вначале случай, когда математическое ожидание исследуемой случайной величины известно и равно 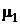. Дисперсия генеральной совокупности X, образованной случайной величиной x, равна .

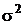В этом случае оценка дисперсии вычисляется по формуле

.

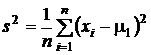П р о в е р и м н е с м е щ е н н о с т ь этой оценки.

.

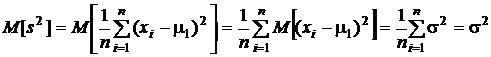Когда математическое ожидание исследуемой случайной величины известно, оценка дисперсии не смещена.

б) Обычно на практике математическое ожидание исследуемой случайной величины неизвестно. В этом случае вместо него приходится использовать оценку, например среднее арифметическое:

.

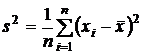П р о в е р и м н е с м е щ е н н о с т ь этой оценки.

.

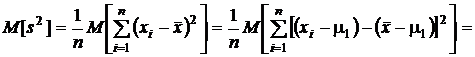
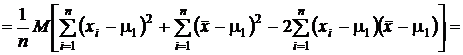
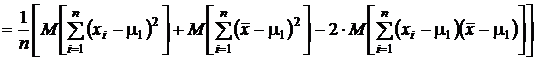Первое слагаемое во внешних квадратных скобках есть сумма дисперсий генеральной совокупности, их в этой сумме n штук, то есть первое слагаемое равно 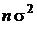. Второе слагаемое есть сумма дисперсий средних арифметических, оно равно 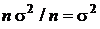. Конструкция вычитаемого сложнее. Рассмотрим его отдельно. Запишем второй сомножитель под знаком суммы в виде:

.

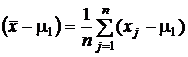В справедливости такой записи можно убедиться, раскрыв скобки и подсчитав каждую сумму по отдельности.

Сделаем подстановку:

.

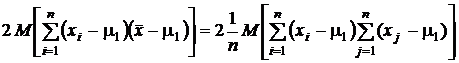Здесь в квадратных скобках суммируются произведения биномов, отличающихся только индексом. В результате внутри квадратных скобок образуется сумма 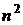слагаемых, среди которых встречаются слагаемые, сомножители которых имеют одинаковые индексы i = j (таких слагаемых nштук), и слагаемые, сомножители которых имеют разные индексы (таких слагаемых 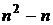штук).

Математическое ожидание каждого слагаемого из первой группы (при i = j)

.

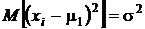Математическое ожидание второй группы слагаемых (при i ¹ j) 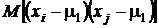есть не что иное, как центральный смешаный момент порядка 1, 1, а это, как следует из разд. 1.7.2, ковариация, которая вследствие независимости выборочных значений равна нулю.

В результате получаем, что

.

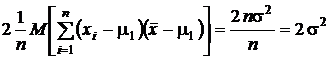Подводя окончательный итог, получаем

.

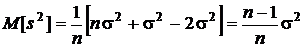Таким образом мы выяснили, что когда математическое ожидание генеральной совокупности неизвестно, исследованная оценка смещена. При n ® ¥ смещение оценки убывает до нуля, поэтому такая оценка является асимптотически несмещенной. Обнаруженное смещение корректируется простым умножением на n/(n – 1), и мы получаем общеизвестную рабочую формулу для расчета несмещенной оценки дисперсии:

.

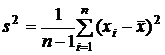Обращает на себя внимание тот факт, что при количестве слагаемых, равном n, сумма делится на n - 1. Это происходит потому, что каждое слагаемое содержит в себе одинаковые выборочные значения с коэффициентом 1/n, которые были использованы при вычислении среднего арифметического значения 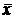, и значит, эти слагаемые не являются независимыми. Чтобы убедиться в этом, найдем ковариацию 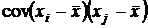. В силу несмещенности среднего арифметического как оценки математического ожидания математические ожидания каждого из этих сомножителей равно 0. Поэтому

,

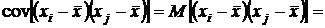
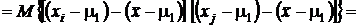
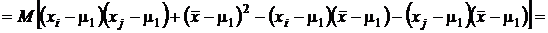
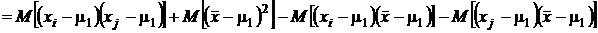где 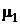– математическое ожидание генеральной совокупности.

Первое слагаемое в последней сумме равно нулю в силу независимости выборочных данных. Второе слагаемое есть дисперсия среднего арифметического, которая равна 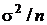. Третье и четвертое слагаемые равны друг другу, поэтому можно записать:

.

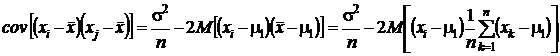Вычитаемое здесь представляет собой сумму произведений биномов. Математическое ожидание всех этих произведений в силу независимости выборочных значений равно нулю, кроме тех, у которых совпадают индексы. Математическое ожидание таких произведений равно дисперсии 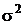, а их количество равно 1. Поэтому

.

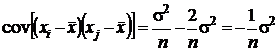Коэффициент корреляции равен

.

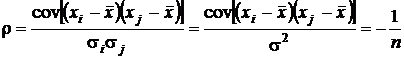Видно, что данные биномы коррелированы, и, значит, зависимы, что и требовалось доказать.

Переведем отмеченное обстоятельство на общепринятый язык математической статистики. Принято говорить, что оценка

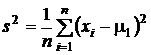
имеет n степеней свободы, а оценка

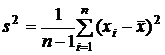
имеет n - 1 степеней свободы.

Этимологию этих понятий можно объяснить следующим образом. Если все выборочные значения независимы, то каждое из них обладает полной “свободой”. На n выборочных значений приходится n таких “свобод”. Столько же “свобод” приходится на n слагаемых первой из приведенных оценок дисперсии.

Как только на слагаемые накладываются какие-либо зависимости, количество “свобод” уменьшается. Во второй оценке степень зависимости между каждыми двумя биномами вида 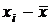мы оценили в 1/n, поэтому в совокупности от всех n таких биномов отнята одна целая “свобода”, и общее количество “свобод” или степеней свободы осталось n - 1. Потому в этой оценке сумма квадратов биномов делится на эквивалентное число оставшихся “свобод”.

Это подтверждается также следующим соображением: по выборке объема n = 1,то есть по одному значению (при этом в знаменателе формулы будет 0) невозможно судить о разбросе значений случайных величин.

в) П л о т н о с т ь р а с п р е д е л е н и я о ц е н к и .

Будем считать, что выборка извлечена из нормальной генеральной совокупности с математическим ожиданием 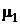и дисперсией .

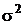Рассмотрим вначале первую из оценок, несмещенную при априори известном математическом ожидании 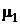. Преобразуем ее следующим образом:

.

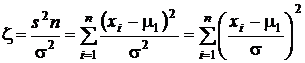Из разд. 1.6.5. следует, что

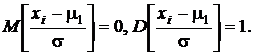
Это значит, что

.

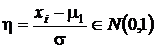В разд. 1.6.7 мы нашли, что при возведении в квадрат нормальной случайной величины с параметрами (0, 1) получается новая случайная величина, плотность распределения и характеристическая функция которой: .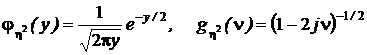

По свойству характеристических функций (см. разд. 1.7.5) характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых. В нашем случае характеристическая функция случайной величины

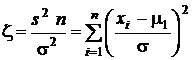
равна 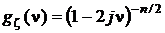. Плотность распределения этой случайной величины отыскивается обратным преобразованием характеристической функции и имеет следующий вид:

.

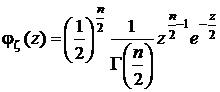В справедливости этого выражения можно убедиться путем определения характеристической функции этой плотности подобно тому, как это было сделано в примере 1 разд. 1.6.7.

Полное название приведенной плотности: плотность распределения “хи-квадрат” с n степенями свободы. Эта плотность распределения имеет всего один параметр n – число степеней свободы.

Принадлежность случайной величины z генеральной совокупности с плотностью распределения “хи-квадрат” и числом степеней свободы n будем обозначать так:

.

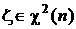Найдем математическое ожидание и дисперсию случайной величины, распределенной по 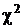с помощью характеристической функции.

Первая производная от характеристической функции по n

,

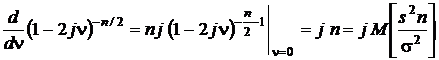откуда

.

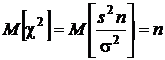Вторая производная

,

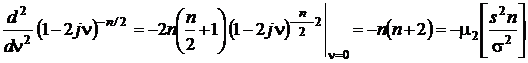откуда

.

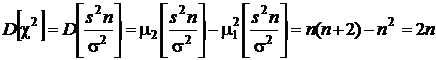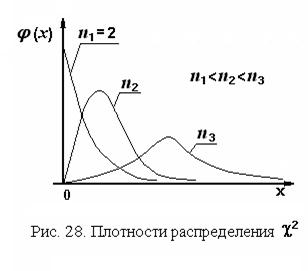В тех случаях, когда оценка дисперсии вычисляется при неизвестном математическом ожидании, количество степеней свободы уменьшается на единицу. Тогда случайная величина zраспределена в соответствии с плотностью распределения 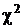с n - 1степенями свободы:

.

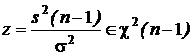Математическое ожидание и дисперсия этой случайной величины

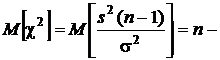1, .

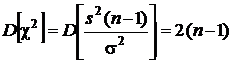Плотность распределения имеет вид

.

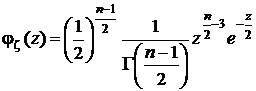Характерная особенность плотности распределения 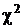: дисперсия равна удвоенному математическому ожиданию.

Плотность распределения 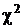безгранично делима. Пусть 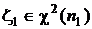с характеристической функцие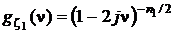й и 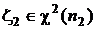с характеристической функцией 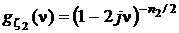. Тогда характеристическая функция случайной величины 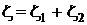есть 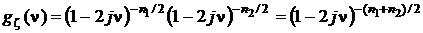, то есть это также характеристическая функция распределения 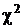с 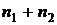степенями свободы, а это значит, что .

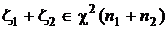Еще раз напомним, что распределение 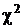получено нами при условии, что выборка изъята из нормальной генеральной совокупности.

В свою очередь, распределение 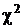асимптотически нормально.

2.3.4.3. Свойства оценки математического ожидания

Случайного вектора

Из многомерной генеральной совокупности X , образованной случайным вектором 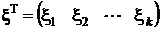с математическим ожиданием 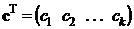и ковариационной матрицей 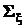извлечена вы­борка векторов 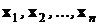, которые попарно независимы в соответствии с исходным требованием математической статистики об обеспечении независимости выборочных данных. Несмещенной состоятельной оценкой математического ожидания 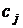каждой компоненты случайного вектора 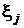, как следует из разд. 2.3.4.1, является среднее арифметическое значение, вычисленное по выборочным значениям соответствующих компонент выборочных векторов:

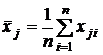, j = 1, 2, ..., k.

Значит, несмещенной состоятельной оценкой математического ожидания является вектор, составленный из таких компонент:

.

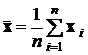Ковариационная матрица этого вектора

.

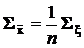Это следует хотя бы из того, что каждый j-й диагональный элемент матрицы 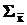, который является дисперсией 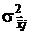каждой j-й компоненты вектора средних арифметических 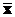, в n раз меньше дисперсии j-го компонента случайного вектора 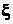, то есть j-го диагонального элемента ковариационной матрицы 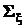(см. разд. 2.3.4.1):

.

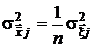Точно так же пропорционально изменяются и остальные элементы матрицы 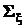, поэтому

.

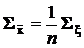2.3.4.4. Оценка ковариационной матрицы случайного вектора

Из многомерной генеральной совокупности X , образованной случайным вектором 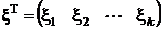с математическим ожиданием 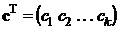и ковариационной матрицей 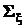, извлечена вы­борка векторов 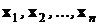, которые попарно независимы в соответствии с исходным требованием математической статистики об обеспечении независимости выборочных данных.

Оценкой ковариационной матрицы 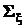является матрица 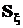той же размерности, диагональные элементы которой – оценки 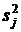диагональных элементов матрицы 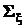, то есть дисперсий 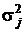j-х компонент случайного вектора ξ. Желательно получить несмещенные оценки этих дисперсий, как и всех остальных элементов матрицы 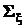, то есть ковариаций.

Вычисление оценки ковариационной матрицы выполняется в соответствии с ее определением (см. разд. 1.8), где вместо символа математического ожидания, как и ранее, используются суммирование и усреднение. Поэтому несмещенная оценка ковариационной матрицы, все элементы которой должны быть несмещенными оценками элементов матрицы 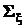, вычисляется по формуле

.

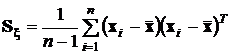В знаменателе этой формулы nуменьшается на единицу, как и в разд. 2.3.4.2, поскольку каждый элемент матрицы 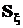“истратил” по одной степени свободы из-за предварительного вычисления среднего арифметического значения соответствующей компоненты. Это понятно и из такого соображения: по выборке объема n = 1 (при этом в знаменателе формулы будет 0) невозможно судить ни о разбросе значений случайных величин, ни о степени их коррелированности. Кроме того, при оценивании ковариационной матрицы необходимо обеспечить, чтобы объем k выборки был не меньше их размерности, то есть чтобы выполнялось неравенство 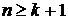, иначе определитель матрицы 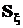будет равен 0, а сама матрица окажется особенной.