Обозначения генеральных моментов и их оценок

Генеральные моменты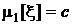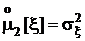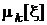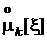
Оценки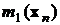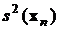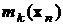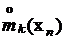

между собой случайным образом при повторении тех же n экспериментов в неизменных условиях, и, значит, являются случайными. Для них, как и для всех случайных величин, могут быть определены такие характеристики, как математическое ожидание, дисперсия, квантили и т.д.

2.3.2.1. Оценивание моментов по выборочной функции распределения

Для получения оценок по выборочной функции распределения воспользуемся интегралом Стилтьеса (см., например, [4]).

Интеграл Стилтьеса определен как предел суммы Стилтьеса:

,

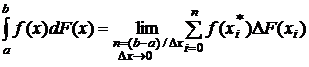где f(x) и F(x) – две ограниченные функции, Dx – ширина участков, на которые разделен интервал [a, b] (если эти участки разной ширины, то тогда Dx – максимальная ширина), 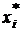– точка внутри i-го участка, 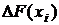– приращение функции F(x) на i-ом участке .

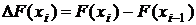Когда функция F(x) дифференцируема везде на[a, b], и ее производная 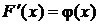, интеграл Стилтьеса обращается в интеграл Римана:

.

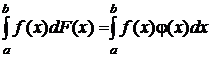Если функция F(x)имеет ступенчатый характер, то есть в точках 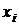она изменяется скачком, а в остальных точках постоянна, то интеграл Стилтьеса вычисляется как сумма:

),

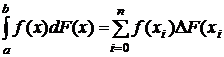где 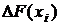– значение скачка функции F(x) в точках .

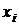Применяя интеграл Стилтьеса для оценки начальных моментов по выборочной функции распределения, по определению моментов (разд. 1.6.2), получим

.

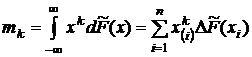Но, как мы выяснили в разд. 2.2, все скачки 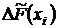выборочной функции распределения в точках 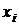одинаковы, равны 1/nи их можно вынести за знак суммы. Кроме того, порядок перечисления слагаемых в сумме, стоящей справа, не имеет значения. Поэтому оценки начальных моментов порядка k вычисляются по формуле

.

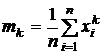В частности, оценкой математического ожидания служит среднее арифметическое:

.

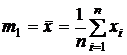Точно так же с помощью интеграла Стилтьеса получим оценки центральных моментов:

.

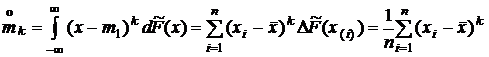В частности, оценка дисперсии вычисляется как

.

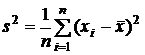Эта же оценка может быть вычислена иначе с применением формулы из разд. 1.6.2:

.

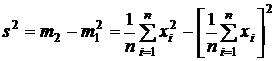Эта формула бывает полезной при вычислении оценок на компьютере в темпе получения данных путем накопления оценок начальных моментов при получении каждого i-го результата измерений. Однако здесь следует предостеречь от опасности, которая заключается в возможности получения отрицательного значения 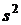. Это может произойти из-за погрешности округления, когда выборочные значения очень велики, а дисперсия генеральной совокупности по сравнению с ними очень мала.

2.3.2.2. Оценивание моментов по выборочной плотности

распределения (по гистограмме)

В отличие от разд. 1.6.2, где определены генеральные моменты, здесь для определения оценок моментов вместо плотности распределения генеральной совокупности будем использовать выборочную плотность, то есть гистограмму (см. рис. 27). В соответствии с математическими определениями генеральных моментов их оценки по гистограмме приобретают иной вид:

оценки начальных моментов

;

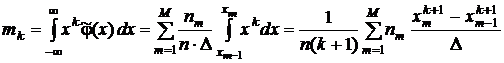оценки центральных моментов

.

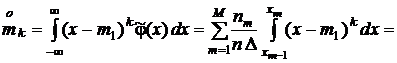
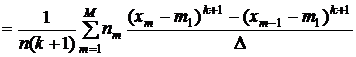Понятно, что потери информации, вызванные группированием выборочных значений при построении гистограммы, снижают качество оценок по сравнению с оценками по выборочной функции распределения.

Пользуясь этими общими формулами, найдем оценки математического ожидания и дисперсии.

.

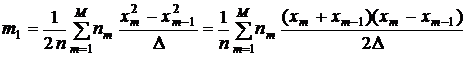Поскольку

, ,

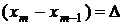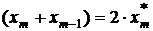где 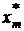– середина m-го отрезка, окончательно получим:

.

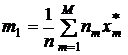Оценка дисперсии.

.

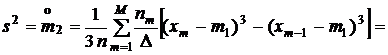
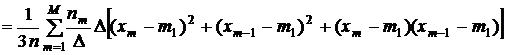Используя равенство 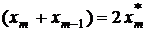, сделаем замены:

, , .

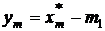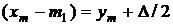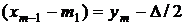Тогда предыдущее равенство упрощается:

.

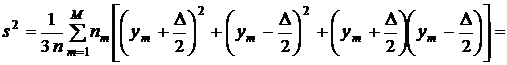
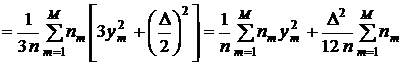Окончательно получим

.

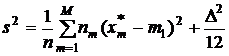Слагаемое 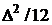называется поправкой Шеппарда.