Линейные функции случайных векторов

Задан общий вид линейной функции случайного вектора:

,

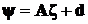где 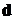– неслучайный вектор, A – квадратная матрица:

.

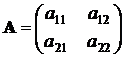Найти математическое ожидание 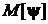и ковариационную матрицу случайного вектора .

,

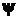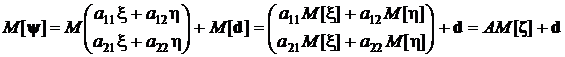то есть, как и ранее, математическое ожидание линейной функции от случайного вектора есть функция от математического ожидания.

Для нахождения ковариационной матрицы вектора 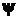воспользуемся математическим определением ковариационной матрицы, приведенным в разд. 1.7.3, и только что полученным выражением для математического ожидания линейной функции случайного вектора:

.

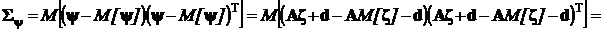
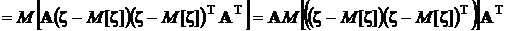В конечном итоге получим важную формулу:

.

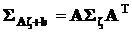Как и ранее, мы видим, что ковариационная матрица не зависит от вектора 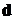, то есть от систематического (не случайного) сдвига случайного вектора.

Возможно так подобрать матрицу A, чтобы ковариационная матрица 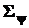оказалась диагональной, и тем самым компоненты вектора 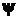– некоррелированными.

Рассмотрим важный частный случай, когда матрица A= (a, b), а вектор 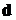состоит из одной компоненты. В этом случае вместо вектора 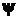имеем скаляр, и рассматриваемое преобразование выглядит следующим образом:

.

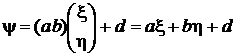Пользуясь только что полученной формулой, получим

.

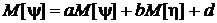Ковариационная матрица (в нашем случае – дисперсия) получается после преобразований, которые мы осуществим по формуле для ковариационной матрицы:

.

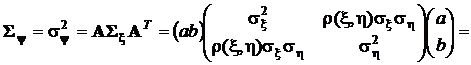
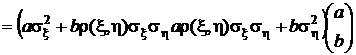Перемножив эти два вектора, окончательно получим

.

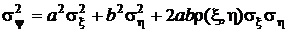В частном случае, когда x и h независимы, дисперсия случайной величины y = ax + bh

.

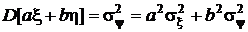Если a = b = 1, эта формула приобретает совсем простой вид и означает, что дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: .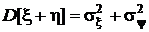

Полученные формулы справедливы вне зависимости от вида плотности распределения участвующих случайных величин.

Характеристическая функция двумерного случайного вектора

Двумерный случайный вектор ζ задан плотностью распределения j(x,y) и в результате “испытаний” принимает значения z.

Обозначение и математическое определение характеристической функции вектора ζ:

,

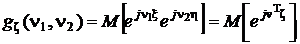где ν – двумерный вектор, с компонентам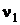и и .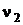

В соответствии с математическим определением математического ожидания

.

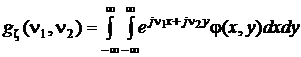Свойства характеристических функций двумерного вектора аналогичны свойствам, которые были установлены в разд. 1.6.4 для характеристических функций случайной величины:

;

;

;

.

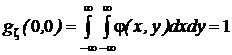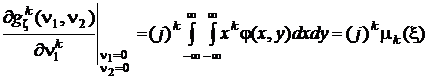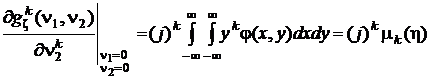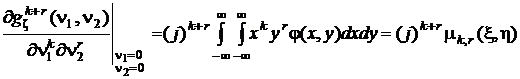К этим свойствам добавляется еще одно. Пусть x и h независимы и y = x + h. Тогда

,

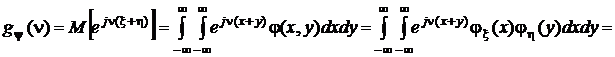
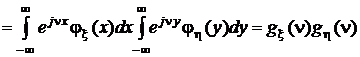то есть характеристическая функция суммы независимых случайных величин равна произведению характеристических функций этих величин.

Это свойство не могло быть обнаружено в разд. 1.6.4, поскольку не была определена совместная плотность распределения случайных величин.

Плотность распределения суммы