Энтропия и информация (по шеннону)

К. Шеннон заложил основы теории информации в интересах научной поддержки систем передачи кодированной информации по каналам связи.

Пусть X – ансамбль возможных сообщений, которые могут быть переданы по каналам связи. Априорные вероятности, с которыми на передающей стороне может появиться i-ое сообщение, обозначим 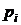= p .

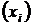В качестве характеристики априорной неопределенности генерации того или иного сообщения на передающей стороне Шеннон предложил применить следующий функционал энтропии:

( ).

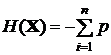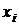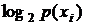В этом функционале используется логарифм по основанию 2 в связи с тем, что в цифровых каналах связи информация обычно представляется в двоичных кодах и энтропия измеряется в битах. Заметим, что единица измерения энтропии – бит отличается от одноименной единицы измерения объема памяти и длины кодовых слов, которая численно равна числу двоичных разрядов слова или количеству разрядов элементарных ячеек памяти компьютера. Так, если ансамбль X состоит из четырех восьмибитовых кодовых слов, вероятности передачи которых одинаковы и равны 1/4, то энтропия этого ансамбля равна 2 битам. Объем памяти, необходимой для хранения этого ансамбля восьмибитовых кодовых слов, равен 32 бит.

Энтропия является характеристикой неопределенности состояния ансамбля X в отличие от характеристики возможности наступления того или иного события, то есть вероятности. Энтропия не зависит от значений, которые может принимать тот или иной элемент ансамбля и от способа его представления. В частности, элементами ансамбля могут быть словесные описания или фотографические изображения. Энтропия характеризует степень хаотичности ансамбля и принимает максимальное значение, когда вероятности 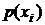одинаковы.

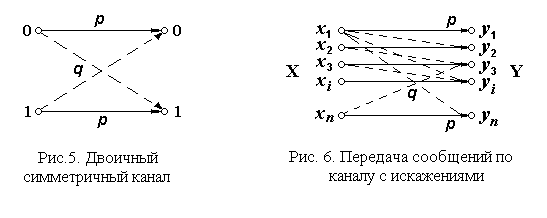
Инструментарий теории информации, выдвинутой К. Шенноном, эффективно используется в теории и практике передачи информации и кодирования. В этих применениях ансамбль X – ансамбль возможных сообщений. Основные результаты теории информации относятся к передаче информации в двоичном коде и к каналам, ориентированным на передачу двоичных кодов. Передача такой информации осуществляется двоичными кодовыми словами, и при каждой такой передаче искажение отдельного символа в передаваемом слове заключается в том, что вместо 1 получатель принимает 0 или вместо 0 получатель принимает 1. При таких условиях канал передачи двоичной информации характеризуется вероятностью искажения символа. Схематическое представление простейшего канала связи, а именно двоичного симметричного канала, представлено на рис 5.

Симметричным этот канал называется потому, что вероятности искажения символов 0 и 1 одинаковы и равны q, как это показано на рисунке. Вероятность p – вероятность неискаженной передачи символа.

Поскольку каждое сообщение 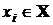передается кодовым словом, которое может состоять из нескольких символов 0 или 1, возможностей искажения слова при передаче по такому каналу гораздо больше (см. рис. 6, где принимаемые сообщения обозначены 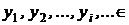Y). Вероятность искажения слова в общем случае отличается от вероятности искажения отдельного символа.

Понятно, что при передаче по каналам связи сообщения (слова) 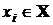и при получении сообщения 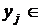Y энтропия ансамбля X, несомненно, уменьшится и будет исчисляться условной энтропией на сообщение

.

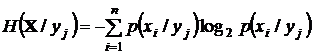Для того чтобы характеризовать всю систему приема-передачи, используют среднюю условную энтропию:

.

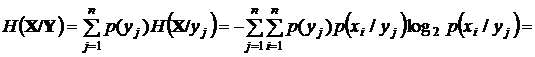
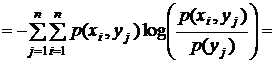
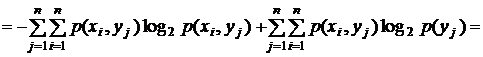
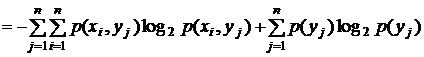Окончательно получим

,

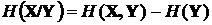где 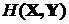– совместная энтропия двух ансамблей, которая, как следует из полученного выражения, равна

.

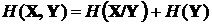Точно так же

, .

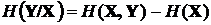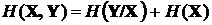Количество информации об 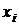, полученное в одном сообщении :

.

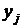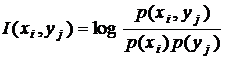Среднее количество информации об X, полученное в сообщении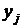

.

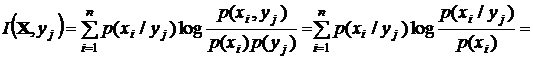
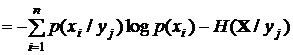Количество информации измеряется в тех же единицах, что и энтропия, – в битах.

Средняя взаимная информация, содержащаяся в Y об X или в X об Y:

,

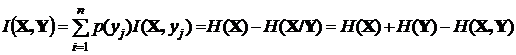то есть это количество информации численно равно количеству неопределенности, устраненной при получении одного сообщения.

Рассмотрим частные случаи.

1. Ансамбль детерминирован, неопределенность отсутствует, поскольку этот ансамбль содержит лишь одну компоненту, то есть .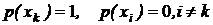

В этом случае H(X)=0, I(X,Y)=0. Это означает, что сообщение об известном факте информации не несет.

2. Сообщения 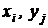независимы, то есть

, , .

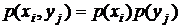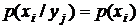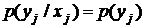Тогда

,

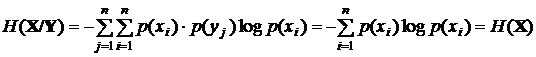откуда следует, что 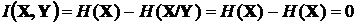, чего и следовало ожидать, ибо независимость 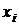и 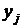означает отсутствие связи, а потому в Y не может содержаться информация об X и наоборот.

3. Связь между элементами X и Y взаимно однозначна, то есть , , .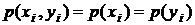

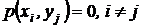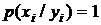В этом случае

.

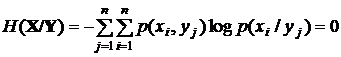Тогда I(X,Y) = H(Х) -H( 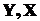)=H(Х). Это значит, что в рассмотренном случае мы имеем дело с идеальным неискажающим каналом связи, и потому количество информации максимально. В общем случае

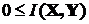£H(X).