Т е о р и я в е р о я т н о с т е й

ОГЛАВЛЕНИЕ

1. Теория вероятностей………………………………………………………………… 7

1.1. Предмет теории вероятностей………………………………………………… 7

1.2. Случайные события и вероятность…………………………………………… 7

1.2.1. Случайные события, виды случайных событий,

основные понятия и определения…………………………………………. 7

1.2.2. Вероятность событий………………………………………………………. 10

1.2.3. Условная вероятность……………………………………………………… 13

1.2.3.1. Формула полной вероятности…………………………………………. 15

1.2.3.2. Формула Байеса………………………………………………………… 15

1.2.4. Последовательность независимых испытаний (схема Бернулли)……… 17

1.3. Дискретные случайные величины……………………………………………. 18

1.3.1. Распределение вероятностей дискретных случайных величин …………. 18

1.3.2. Биномиальное распределение вероятностей……………………………… 20

1.3.3. Числовые характеристики …………………………………………………. 22

1.3.4. Моменты функций от случайных величин……………………………….. 25

1.3.5. Производящая функция моментов …………………………………….….. 26

1.3.6. Теорема Пуассона…………………………………………………………… 28

1.3.7. Локальная теорема Муавра – Лапласа…………………………………….. 29

1.4. Двумерные дискретные случайные величины……………………………….. 30

1.4.1. Распределение вероятностей………………………………………………. 30

1.4.2. Числовые характеристики…………………………………………………. 32

1.4.3. Линейное преобразование случайного вектора. Числовые

характеристики…………………..………………………………………….. 36

1.4.4. Производящая функция моментов двумерного случайного

вектора………………………………………………………………………... 37

1.5. Энтропия и информация (по Шеннону)…………………………………… 39

1.6. Непрерывные случайные величины………………………………………….... 43

1.6.1. Функция распределения и плотность распределения вероятностей……... 44

1.6.2. Числовые характеристики ………………………………………..………… 46

1.6.3. Дифференциальная (относительная) энтропия…………………………... 52

1.6.4. Характеристическая функция непрерывной случайной величины……… 54

1.6.5. Линейные функции непрерывных случайных величин………………..…. 56

1.6.6. Примеры плотности распределения непрерывных случайных величин… 57

1.6.6.1. Случайная величина – интервал времени между импульсами

в простейшем потоке……………………………………………………... 57

1.6.6.2. Равномерная плотность распределения………………………………… 61

1.6.6.3. Плотность распределения Arcsin……………………………………….. 62

1.6.6.4. Нормальная плотность распределения (Гаусса)………………………. 63

1.6.6.5. Плотность распределения Лапласа…………………………………….. 67

1.6.6.6. Плотность распределения Коши……………………………………….. 69

1.6.6.7. Экспоненциальное семейство распределений…………………………. 70

1.6.7. Функции от непрерывных случайных величин…………………………… 71

1.6.8. Неравенство Чебышева………………………………….…………………. 76

1.7. Двумерные непрерывные случайные величины (двумерные

случайные векторы) …………………………………………………………….. 78

1.7.1. Функции распределения и плотности распределения……………………. 78

1.7.2. Числовые характеристики………………………………………………….. 81

1.7.3. Ковариационная матрица случайного вектора……………………………. 85

1.7.4. Линейные функции случайных векторов………………………………….. 86

1.7.5. Характеристическая функция двумерного случайного вектора………….. 88

1.7.6. Плотность распределения суммы двух независимых

случайных величин…………………………………………………………. 89

1.7.7. Двумерная нормальная плотность распределения……………………….. 90

1.8. Многомерный случайный вектор …………………………………………… 95

2. Математическая статистика………………………………………………………… 98

2.1. Задачи математической статистики…………………………………………… 98

2.2. Кондиционирование результатов экспериментов……………………………. 99

2..3. Точечное оценивание………………………………………………………….. 102

2.3.1. Оценивание квантилей……………………………………………………… 102

2.3.2. Точечное оценивание моментов…………………………………………… 104

2.3.2.1. Оценивание моментов по выборочной функции распределения……. 105

2.3.2.2. Оценивание моментов по выборочной плотности

распределения (по гистограмме)………………………………………. 106

2.3.3. Оценивание параметров законов распределения…………………………. 108

2.3.4. Свойства точечных оценок…………………………………………………. 109

2.3.4.1. Свойства оценок математического ожидания ………………………… 110

2.3.4.2. Свойства оценок дисперсии…………………………………………….. 113

2.3.4.3. Свойства оценки математического ожидания случайного вектора…. 120

2.3.4.4. Оценка ковариационной матрицы случайного вектора………………. 121

2.3.5. Метод максимального правдоподобия…………………………………….. 122

2.3.6. Метод минимума 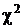……………………………………………………….. 126

2.3.7. Оценивание коэффициентов аппроксимирующих полиномов………….. 128

2.3.7.1. Формулировка задачи………………………………………………….. 128

2.3.7.2. Измерения однократные……………………………………………….. 131

2.3.7.3. Плотность распределения величины 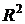…………………………….. 135

2.3.7.4. Практически важные замечания………………………………………. 136

2.3.7.5. Измерения многократные, характеристики погрешностей известны.. 138

2.3.7.6. Измерения многократные, характеристики погрешностей

неизвестны……………………………………………………………… 140

2.3.7.7. Особенности вычислений при реализации МНК и ОМНК………….. 143

2.3.7.8. Основные принципы планирования эксперимента, выполняемого

с целью полиномиальной аппроксимации…………………………….. 145

2.3.7.9. Расширение класса аппроксимирующих полиномов…………………. 146

2.4. Интервальное оценивание……………………………………………………… 147

2.4.1. Постановка задачи…………………………………………………………… 147

2.4.2. Доверительный интервал для вероятности………………………………… 148

2.4.3. Доверительный интервал для математического ожидания.

Дисперсия генеральной совокупности известна…………………………… 151

2.4.4. Доверительный интервал для математического ожидания.

Дисперсия генеральной совокупности неизвестна………………………… 152

2.4.5. Доверительный интервал для дисперсии………………………………….. 154

2.4.6. Доверительные интервалы для интерквантильного промежутка……….. 155

2.4.6.1. Параметрические толерантные пределы………………………………. 155

2.4.6.2. Непараметрические толерантные пределы……………………………. 158

2.4.7. Бутстреп – оценивание……………………………………………………… 164

2.5. Статистические методы проверки гипотез…………………………………… 167

2.5.1. Постановка задачи и общие принципы…………………………………… 167

2.5.2. Критическая область и критическое значение……………………………. 168

2.5.3. Простые гипотезы…………………………………………………………… 170

2.5.4. Сложные гипотезы…………………………………………………………... 172

2.5.5. Проверка гипотезы о виде плотности распределения…………………….. 174

2.5.5.1. Критерий “хи - квадрат”………………………………………………… 174

2.5.5.2. Критерий Колмогорова – Смирнова…………………………………… 179

2.5.5.3. Критерий 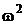Мизеса…………………………………………………… 181

2.5.6. Проверка гипотез при полиномиальной аппроксимации………………… 183

2.5.6.1. Критерий Кочрена проверки гипотезы о равенстве дисперсий……… 183

2.5.6.2. Проверка гипотезы о степени аппроксимирующего полинома,

характеристики погрешностей измерений известны………………… 184

2.5.6.3. Проверка гипотезы о степени аппроксимирующего полинома,

характеристики погрешностей измерений неизвестны………………. 188

2.6. Последовательная полиномиальная аппроксимация

с проверкой гипотезы о степени полинома…………………………………… 191

2.7. Проверка сложных гипотез о числовых характеристиках случайных

величин с контролем вероятностей ошибок первого и второго рода……….. 194

2.7.1. Основные положения……………………………………………………….. 194

2.7.2. Проверка сложной гипотезы о математическом ожидании………………. 195

2.7.3. Проверка сложной гипотезы о дисперсии…………………………………. 201

2.7.4. Проверка сложной гипотезы об интерквантильном промежутке………… 204

2.7.5. Проверка сложной гипотезы о числовых характеристиках

случайных величин с применением доверительных интервалов,

построенных методом бутстреп……………………………………………. 208

2.7.6. Проверка сложной гипотезы о вероятности методом статистического

последовательного анализа………………………………………………… 209

Библиографический список……………………………………………………………. 212

ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Теория вероятностей занимается установлением макрозакономерностей, которым подчиняются массовые однородные случайные события. Теория вероятностей не стремится предсказать единичное событие.

Однородные события – события, которые происходят при осуществлении одних и тех же условий S и подчиняются определенным макрозакономерностям независимо от природы событий.

Условия S необходимо подробно и тщательно описывать в каждом конкретном случае при постановке задаче исследования случайных событий.

Вероятность событий

Вероятность (осуществления) события – числовая характеристика возможности события при условиях S. Если 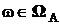, то вероятность события А есть вероятностная мера множества 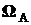, обозначается P(A).

Приведем математические определения вероятности события.

К л а с с и ч е с к о е о п р е д е л е н и е:

P(A) есть отношение количества случаев, благоприятствующих появлению события A, к общему числу испытаний.

Ч а с т о т н о е о п р е д е л е н и е:

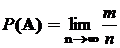
где n – общее число выполненных испытаний, m – количество случаев появления события A при этих испытаниях.

С о в р е м е н н а я а к с и о м а т и к а (А. Н. Колмогоров):

P(A) – неотрицательная монотонная счетно-аддитивная мера возможности случайного события, такая, что P(T) = 1.

Пояснения к этой аксиоматике:

неотрицательность: P(A) ³0;

монотонность: если A Ì B тоP(A) £P(B), то есть, если при наступлении события A обязательно наступает событие B, но обратное необязательно, то P(A) £P(B);

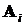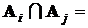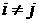счетная аддитивность: если условия S определены, события попарно несовместны, то есть Æ, , то

.

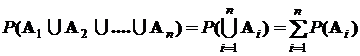В современной теории вероятностная мера определяется на классах событий. Классы событий образуются таким образом, чтобы они давали возможность определить вероятностную меру вначале на простейших событиях, а затем распространить ее на события любой сложности. Для этого класс событий должен содержать в себе не только сходящиеся в этом классе последовательности событий, но также их пределы. Обозначим класс событий Â.

Если в условиях Sсобытия 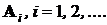принадлежат классу событий Â, и счетное объединение и счетное пересечение этих событий также принадлежит этому классу, то есть

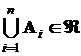и ,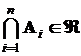

то этот класс событий называется алгеброй событий.

Если в этих же условиях 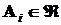, 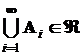и 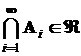, то такой класс событий называется сигма-алгеброй (s-алгеброй).

П р и м е р и з п л а н и м е т р и и. Класс всех многоугольников образует алгебру многоугольников, поскольку пересечение счетного количества многоугольников есть также многоугольник. Дополнение этого класса бесконечными пересечениями и объединениями многоугольников, что мы делали для определения меры (площади) круга, привело к образованию сигма-алгебры, и это позволило с помощью предельного перехода распространить меру (площадь) на геометрические фигуры, которые не являются многоугольниками, но суть пределы, к которым стремятся бесконечные сходящиеся последовательности многоугольников при их объединении и пересечении.

В итоге в соответствии с современной аксиоматикой теории вероятностей говорят, что случайные события и вероятностная мера этих событий определены тройкой: (W, Â,P), где фигурируют введенные обозначения пространства элементарных событий, сигма-алгебры событий и вероятностной меры на них [4].

Для иллюстрации введенных понятий и свойств вероятностной меры, как было указано ранее, прибегают к геометрическому представлению событий в виде замкнутых фигур внутри прямоугольника, который представляет собой пространство элементарных событий W. Вероятностная мера событий отождествляется с площадью соответствующих фигур с учетом того, что вероятностная мера всего прямоугольника равна единице.

Это представление событий и вероятностей показано на рис. 1, который иллюстрирует свойства монотонности (рис. 1, а) и счетной аддитивности (рис. 1, б) вероятностной меры.

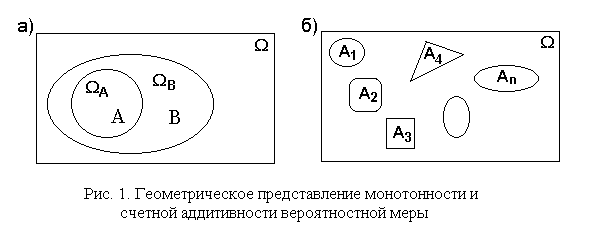
Из аксиоматики Колмогорова следует:

а) ;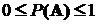

б) 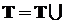Æ,откуда следует: P(T)=1=P(T)+P(Æ)=1+P(Æ),

и, наконец, P(Æ)=0;

в) AÎW, B ÎW, AиBпротивоположны, то есть A 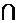B = Æ, A 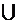B = Т;

тогда P(A 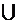B) =P(A)+P(B) =P(T) =1,откуда 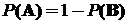, то есть

, ;

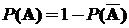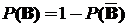г) пусть AÎW, B ÎWисобытия пересекаются, то есть 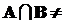Æ.

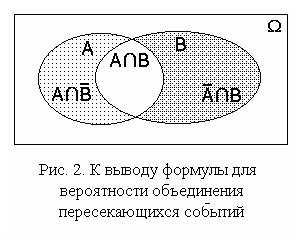В этом случае вероятность объединения событий не равна сумме вероятностей. Для вывода формулы представим объединение пересекающихся событий A и B в виде объединения трех непересекающихся событий (рис. 2): .

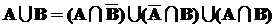Точно так же представим события

A и B: , .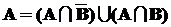

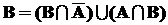К этим выражениям можно применить аксиому счетной аддитивности вероятностной меры:

,

, ,

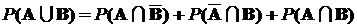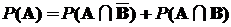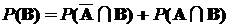откуда следует, что 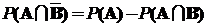и .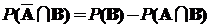

Подставляя эти два выражения в первое, окончательно получим

=

= .

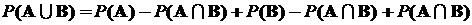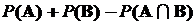Очевидно, что в случаях, когда события несовместны, то есть не пересекаются,

,

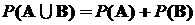а в общем случае всегда .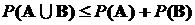

Условная вероятность

Пусть, как всегда, A 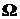Ì , B Ì 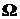и сформулированы условия S.

Условная вероятность есть вероятность осуществления одного из событий при условии, что другое событие состоялось. Обозначение условных вероятностей:

P(B/A) – условная вероятность события B при условии осуществления события A;

P(A/B) – условная вероятность события A при условии осуществления события B.

Найдем условную вероятность, например, P(B/A)с помощью классического определения вероятности по разд. 1.2.2. Для этого необходимо знать общее количество n предполагаемых испытаний, в результате которых могут осуществиться события A, B, A 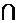B.

Общее количество исходов, при которых возможна реализация условного событияB/A, определяется исключительно числом появления события A, поскольку если оно не осуществится, то не осуществится и условное событиеB/A.Пусть m – число исходов, благоприятствующих появлению события A. Понятно, что в общем случае .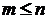

В результате предполагаемых испытаний событие B может появиться и без появления события A, но условное событие B/A осуществляется только при совместном появлении событий A и B. В связи с этим число случаев, благоприятствующих появлению событияA 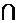B,равно количеству случаев, благоприятствующих появлению события B/Aили события A/B.Обозначим это количество s.

Тогда в соответствии с классическим определением вероятности

P(В/А)= ,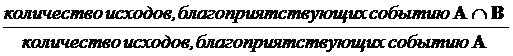

то есть

.

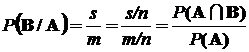Таким образом, условная вероятность P(В/А) определяется, как

.

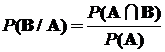Точно так же

.

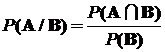Из полученных выражений следует, что

.

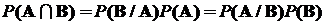События A и B независимы, когда P(B/A)=P(B) и P(A/B)=P(A).

Отсюда следует формулировка признака независимости случайных событий:

события A и Bнезависимы тогда и только тогда, когда

P(A 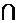B)=P(A)P(B).

В самом деле, при таком соотношении

.

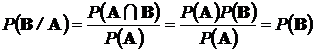Если A и Bсвязаны взаимно однозначно, тоm=s, а потому

P(A 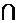B)=P(A)=P(B),P(B/A)=1,P(A/B)=1.

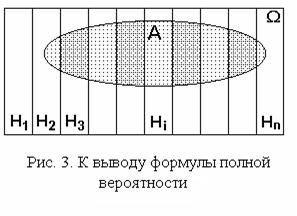
1.2.3.1. Формула полной вероятности

Пусть при условиях S в 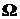возможно событие A. Кроме того в 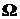определена полная группа попарно непересекающихся событий 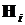, i=1, 2, ..., n, то есть

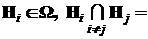Æ, .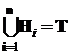

Данная ситуация представлена на рис. 3. Из предъявленных соотношений следует, что

.

Воспользовавшись аксиомой Колмогорова о счетной аддитивности вероятностной меры и математическим определением условных вероятностей, получим:

.

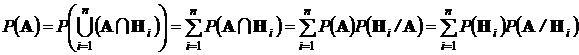Таким образом получена формула полной вероятности:

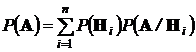
в которой события 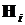именуются гипотезами.

1.2.3.2. Формула Байеса

Воспользовавшись формулой условной вероятности и формулой полной вероятности, получим ценную для многочисленных приложений формулу Байеса:

.

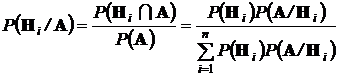Формула Байеса эффективно используется при исследованиях природных явлений, при исследованиях и испытаниях рукотворных объектов в условиях неопределенности математической модели исследуемых объектов и действия мешающих случайных воздействий. В этих условиях события, происходящие при исследованиях, неоднозначно связаны со свойствами и параметрами объектов.

Пусть 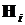– гипотезы (предположения) исследователя о свойствах или параметрах исследуемого объекта, рукотворного или природного. Эти гипотезы могут иметь одинаковый или различный приоритет, который выражается путем задания значений вероятностей 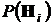. Эти вероятности в данной ситуации суть априорные вероятности гипотез .

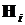В результате эксперимента или исследования событиеA происходит с той или иной вероятностью. Это событие исследователь фиксирует, и по нему он должен вынести суждение об оправданности того или иного априорного предположения (гипотезы). В силу действия случайных факторов и неопределенности математической модели объекта однозначные причинно-следственные связи между предположениями (гипотезами) исследователя и результатами испытаний размыты. После выполнения эксперимента (испытания) фиксируется событие A. В этой ситуации можно оценить условные вероятности 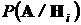возможности реализации события A при справедливости каждой из гипотез. Таким образом после эксперимента правая часть формулы Байеса может быть рассчитана, и формула Байеса дает возможность оценить апостериорную вероятность той или иной гипотезы при условии, что результатом эксперимента оказалось событие A.

Естественно принять в качестве наиболее правдоподобного то предположение (гипотезу), апостериорная вероятность которого окажется наибольшей. Такое правило принятия решения, которое основано на применении формулы Байеса, называется байесовским. Этой же формулой порожден принцип максимума апостериорной вероятности, который часто и эффективно используется в теории и практике систем автоматического регулирования, при математической обработке результатов измерений, при идентификации объектов.

Наиболее широкое применение байесовский принцип максимума апостериорной информации находит в системах передачи информации по каналам связи, в которых велика вероятность искажения передаваемых символов и сообщений. Обычно это цифровые каналы. В них на передающей стороне применяется избыточное кодирование сообщений, а на приемной стороне устанавливается байесовский декодер, реализующий указанный байесовский принцип в реальном времени.

Числовые характеристики

Распределение вероятностей случайной величины – это максимально полная ее характеристика, но в то же время очень громоздкая. Кроме того вид распределения реальных случайных величин, которые порождаются техническими причинами в измерительных системах, системах автоматизации, системах передачи и приема информации, чувствителен к неконтролируемым случайным факторам. Поэтому в технических приложениях чаще всего используются не распределения вероятностей, а числовые характеристики расположения случайной величины на числовой оси, разброса ее значений и других свойств.

В качестве таких характеристик применяются моменты распределения вероятностей. Это название вызывает естественное желание применить механическую модель, которой мы будем пользоваться при изложении нижеследующего материала.

Механическая система, моделирующая распределение вероятностей, может быть представлена в виде жесткого невесомого стержня (числовая ось), на которую нанизаны точечные массы, расположенные в точках 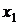, ,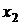..., . 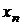Значения вероятностей 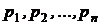моделируются, как значения массы (или веса) этих точек. Таким образом эти точечные массы придают описанной механической системе вращающий момент относительно начала координат.

В качестве характеристики расположения всех значений случайной величины на оси естественно использовать координату центра тяжести описанной механической системы. Как известно из теоретической механики, координата центра тяжести системы определяется из условия равенства моментов: вращающего момента, создаваемого точечными массами, и противодействующего момента, который должна создавать равнодействующая сила, приложенная к центру тяжести.

Итак, пусть 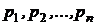– веса точечных масс, то есть силы, создаю­щие вращающий момент относительно начала координат. Тогда отрезки [0, 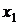], [0, 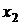], ..., [0, 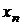] – плечи. Равнодействующая сила равна сумме сил, создаваемых точечными массами. Если 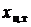– координата центра тяжести, то отрезок [0, 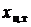] – плечо равнодействующей силы. Уравнение моментов имеет вид

, .

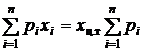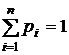Отсюда следует, что

,

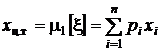где 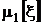– первая из характеристик распределения вероятностей и самой случайной величины, которая имеет два равноправных названия: математическое ожидание случайной величины x и первый начальный момент случайной величины x. Для обозначения математического ожидания используют также равноправное обозначениеM[x].

Рассеяние, разбросанность по числовой оси построенной нами механической системы – аналога распределения вероятностей – не зависит от расположения центра тяжести и характеризуется моментом инерции системы относительно ее центра тяжести. Напомним, что момент инерции точки относительно оси вращения пропорционален массе точки и квадрату ее расстояния от оси. Применительно к распределению вероятностей эта характеристика называется вторым центральным моментом распределения (слу­чайной величины) или дисперсией случайной величины, вычисляется по очевидной формуле для моментов инерции и имеет несколько равноправных обозначений:

,

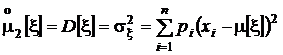где 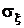– среднеквадратическое значение (отклонение) случайной величины.

Понятно, что если величина не случайна, а потому в любых обстоятельствах может принимать только одно значение с вероятностью 1, то ее дисперсия будет равна нулю.

Кружок над обозначением момента означает, что этот момент вычисляется относительно центра тяжести.

В теории вероятностей, в отличие от механики, широко используются начальные и центральные моменты более высокого порядка:

начальные моменты порядка k : ;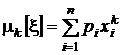

центральные моменты порядка k: .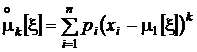

Найдем несколько полезных соотношений. Вначале вычислим первый центральный момент:

,

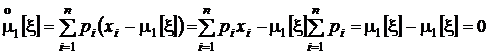чего и следовало ожидать.

Найдем теперь соотношение между вторыми моментами: начальным и центральным.

= .

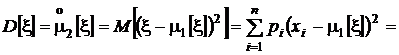
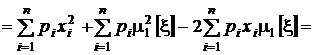
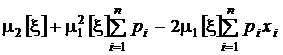Поскольку 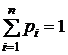и 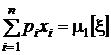, окончательно получим

.

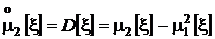Размерность моментов k-го порядка есть k-ая степень размерности значений, которые принимает случайная величина. Например, размерность дисперсии есть квадрат размерности значений случайной величины.

Теорема Пуассона

Проанализируем асимптотическое поведение вероятности появления m событий в схеме Бернулли при n ® ¥, np=const= a. Цель – упрощение вычислений, трудоемкость которых сильно возрастает с ростом n.

Задача состоит в нахождении предела последовательности:

.

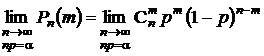Из равенства np =a следует, что p = 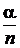. Кроме того,

.

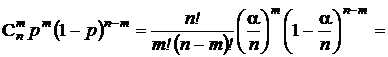
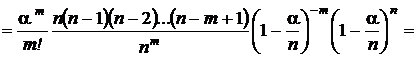
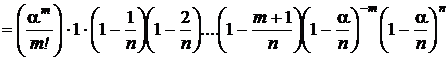В полученном выражении первый сомножитель не содержит n.Предел последнего сомножителя при n ® ¥равен 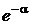. Пределы остальных сомножителей при n ® ¥равны 1. В результате получаем асимтотическое представление вероятностей из схемы Бернулли, или, что то же самое, биномиального распределения, в виде

.

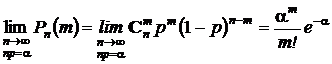Этот результат получен Пуассоном и успешно применяется для расчета вероятностей редких событий (при n ® ¥вероятность p стремится к 0) при массовых явлениях (испытаниях, опытах).

Полученные предельные значения вероятностей образуют в совокупности распределение вероятностей случайной величины. В самом деле,

.

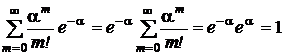Это распределение называется распределением Пуассона. Математическое ожидание и дисперсия этой случайной величины равны

M[m] = D[m] = a = np.

Производящая функция распределения Пуассона:

.

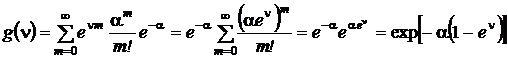1.3.7. Локальная теорема Муавра-Лапласа

В отличие от теоремы Пуассона теорема Муавра-Лапласа посвящена установлению асимптотики для вероятностей событий по схеме Бернулли при n ® ¥ и при p = const.

Здесь без вывода и доказательства приводится результат, полученный Муавром и Лапласом.

Напомним, что в разд. 1.3.5 были получены следующие выражения для математического ожидания и дисперсии случайной величины: числа появления события A при n испытаниях по схеме Бернулли

M[m] = np, D[m] = npq = np(1-p),

где p – вероятность появления события A при одном испытании.

В соответствии с локальной теоремой Муавра-Лапласа значения вероятностей 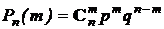при n ® ¥и p = constаппроксимируются функцией

.

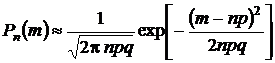Эта функция симметрична и имеет максимум при m = np.

Распределение вероятностей

Будем рассматривать двумерную случайную величину как двумерный случайный вектор

.

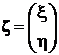Компонентами вектора ζ являются дискретные случайные величины x и h, которые могут принимать значения 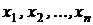и 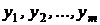соответственно. Реализации вектора ζ будем обозначать вектором z.

При каждом испытании компоненты вектора ζ могут принимать значения 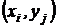с вероятностью совместного осуществления двух событий 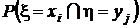. В дальнейшем будем пользоваться упрощенными обозначениями этой вероятности в виде 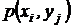или .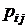

Кроме того, заметим, что события 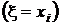образуют полную группу попарно несовместных событий. То же самое можно утверждать и о событиях .

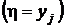Представим совместное распределение вероятностей 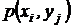в виде таблицы 1.

События 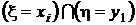, , 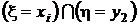..., 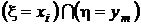не пересекаются, а их объединение есть не что иное, как событие 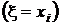. Поэтому, суммируя элементы этой таблицы по строкам, в соответствии с аксиомой аддитивности (см. разд. 1.2.2) получим значения вероятностей 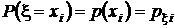. По этой же причине суммирование элементов таблицы по столбцам даст значения вероятностей .

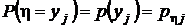Таблица 1

Числовые характеристики

Числовые характеристики, а именно моменты отдельных составляющих вектора ζ определяются через маргинальные (частные) распределения точно так же, как для одномерной (скалярной) дискретной случайной величины:

начальные моменты k-го порядка

, ,

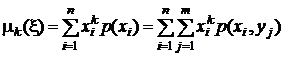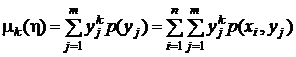в частности, математические ожидания

, ;

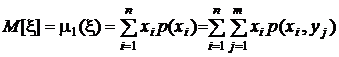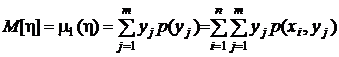центральные моменты k-го порядка

,

,

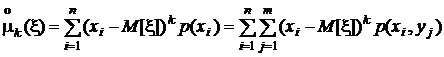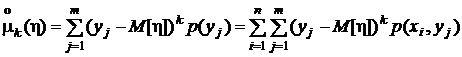в частности, дисперсии

,

.

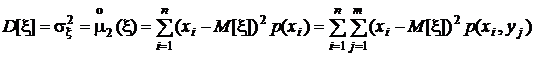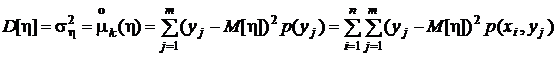Для составляющих случайного вектора определены смешанные моменты:

начальные моменты порядка k, r

;

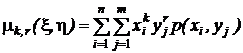центральные моменты порядка k, r

.

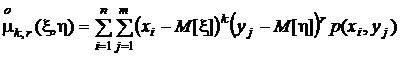Особое значение для дальнейшего имеет центральный смешанный момент порядка (1, 1),который называется корреляционным моментом или ковариацией:

.

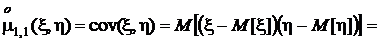
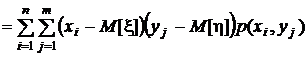Для того чтобы установить соотношение между центральным и начальным смешанными моментами раскроем скобки в последнем выражении и выполним несложные преобразования:

.

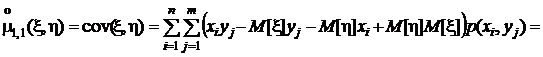
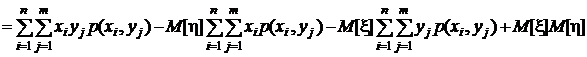Окончательно получим .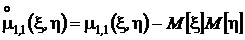

Если x и h независимы, то

.

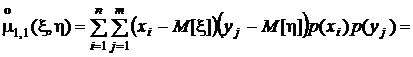
Но, как было установлено в разд. 1.3.3, 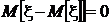и 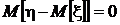, поэтому центральный смешанный момент 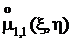независимых случайных величин равен нулю. Однако из того, что 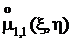=0, независимость случайных величин x и h,вообще говоря,не следует. О случайных величинах, корреляционный момент которых равен нулю, говорят, что они не коррелированы. Для оценки степени коррелированности случайных величин в приложениях удобнее использовать безразмерный коэффициент корреляции 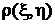. Его значение не зависит от масштаба, в котором выражены значения случайных величин:

.

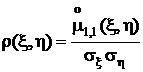С целью определения диапазона значений коэффициента корреляции рассмотрим крайний случай взаимно однозначной зависимости между x и h,а именно допустим, что h = ax + b. Другой крайний случай, а именно независимость x и h,рассмотрен ранее в настоящем разделе.

Из предположен