Асимптотическая формула Пуассона и условия ее применимости.

Пример.

Теорема. Пусть проведено n повторных независимых испытаний, в каждом из

которых события А наступает с вер-тью р, причем 1)число испытаний достаточно

велико (n³100) 2)Величина l=np£10, тогда вер-ть Pm,n того, что в этих испытаниях

событие А наступит m раз вычисл. по след. приближ. ф-ле:

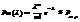
Интегральная теорема Муавра—Лапласа и условия ее применимости. Функция Лапласа Ф(х) и ее свойства. Пример.

Т.: Пусть проведено n повторных независимых испытаний, в каждом из которых некоторое событие А наступает с вер-тью р, причём. 1)число испытаний достаточно велико. 2)Значение npq³20. ; Тогда вер-ть того, что число m наступлений событий А в этих испытаниях окажется заключено в границах от m1 до m2 вычисляется по след. приближ. ф-ле.

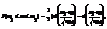
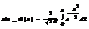
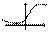
Св-ва функции Лапласа.1)Нечётность Ф(-х)=-Ф(х); 2)Монотонно возрастающая Ф(х); 3)limФ(х)=1 {где хà+¥}; limФ(x)=-1 {где хà-¥}. На практике: если х³5, полагаем что Ф(х)»1 График у=Ф(х) в пределах от –1 до 1.

Следствия из интегральной теоремы Муавра—Лапласа (с выводом). Примеры.

Пусть выполнили условие применимости интегральной теоремы М.Лапласа, тогда: 1)Вер0ть того, что число m наступлений события А в n испытаниях отличается от величины np не более, чем на эпсило (E) (по абсолютной величине) вычисл. По след. ф-ле:

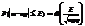
2)Вер-ть того что частость (доля) m/n наступлений событий А в n испытаниях отличается от вер-ти р не более чем на D (по абсолютной величине) вычисл. По след. ф-ле: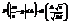

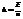
12. Понятие случайной величины и ее описание. Дискретная случайная величина и ее закон (ряд) распределения. Независимые случайные величины. Примеры.

Опр.: Случайной величиной называется переменная, кот. В рез-те испытания принимает то или иное числовое значение. Пр1)число попаданий в мишень ßдис-кретная случ. величина;Пр2) рост человекаßнепрерывная случ. величина.; Опр. Случайная величина назыв. дискретной, если число её возможных значений конечно или счётно (множество счетное, если его можно перенумеровать натур. числами).Опред. Законом распределения с.в.наз-ся всякое соотношение, устанавливающее связь между возможными значениями с.в.и соответствующими вер-тями. Для дискретной с.в.закон распр.может быть дан задан в виде табл., в виде формулы, графчески.

Xi	X1	X2	…	Xk
Pi	P1	P2	…	Pk

Следствие: Из определения закона распределения следует что события (Х=х),…,

(Х=хк) –образуют полн. Систему. => Р(Х=х1)+…+Р(Х=хк)=1 р1+р2+…+рк=1

ßосновное св-во закона распределения.

Две с.в.наз-ся независимыми, Если закон распределения одной из них не меняется от того, какие значения приняла другая величина.

13. Математические операции над дискретными случайными величинами и примеры Построения законов распределения для kХ, Х2 , Х+Y, XY по заданным распределениям независимых случайных величин Х и Y.

Произведением kX с.в.X на постоянную величину k,наз-ся с.в.,которая принимает значения kx_i с теми же вер-тями p_i(i=1,2…n)

m-степенью с.в.X,т.е.X^m, наз-ся с.в., которая принимает значения x^m_i с теми же вер-тями p_i.

Суммой (разностью или произведением) с.в.X иY наз-ся с.в.,которая принимает все возможные значения вида x_i+y_j (x_i-y_j или x_i*y_j), где i=1,2..n j=1..m с вероятностями p_ij того что с.в.X примет значение x_j, а Y - значение y_i

pij=P[(X=xi)(Y=yj)]

если с.в.независимы, то по теореме умножения вер-тей для независимых событий

pij=P(X=xi)·P(Y=yj)=pi·pj

Математическое ожидание дискретной случайной величины и его свойства (с выводом). Примеры.

Опр. Математическим ожидание M(X) дискретной с.в. X наз-ся сумма произведений всех её значений на соответствующие им вер-ти

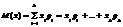Св-ва.

1) М(С)=С, где С- пост. случ. величина.

2)М(aх)=aМ(х); a-некоторое число.

3)М(Х±Y)=М(X)±M(Y). 4)Пусть случ. вели-чины X иY- независимы, тогда М(XY)=M(X)M(Y).

5)Пусть х1,…,хn- случ. вели-чины такие, что M(x1)=…=M(xn)=a; M((x1+…+xn)/n)=a

Дисперсия дискретной случайной величины и ее свойства (с выводом). Примеры.

Опр.Дисперсия D(X) с.в.X наз-ся матем.ожид.квадрата её отклонения от матем.ожид.

D(X)=M(X-M(X))

Свойства.

1) D(C)=0

2) D(kX)=k²D(X)

3) D(X)=M(X²)-[M(X)]²

4) D(X±Y)=D(X)+D(Y)