Статистическое определение вер-ти.

Пусть проведено n-испытаний, в которых событие А наступило m раз, тогда отношение (m/n) назыв. Частностью наступления события А в n испытаниях. Опр.: Пусть условия проведения некоторого испытания можно с точностью произвести неограниченное число раз, тогда вер-тью P(A) наступления события А в одном испытании назыв. Такое число, около которого группируются значения частности (m/n) при неограниченном увеличении числа испытаний n. ,т.е. P(A)=lim(m/n). (На практике полагают P(A)»(m/n) при достаточно большом n) Следствие:

0£m£n; 0£(m/n)£1; lim0£lim(m/n)£lim1 ; 0£P(A)£1.Условия:* соят.долж.быть исходами только тех испы-й, кот.могут быть вопроизвед.неогранич.число раз при одноми томже комплексе усл.

* соб-е должно обладать статистической устойчивостью

* число испытаний должно быть достаточно велико

Пр. Студ.идёт сдаватьэкз.по т.в. «С како вер-ю он сдаст экз?правельно поставлен вопрос для опред стат.вер.? нет, нет воспроизвед.одних и тех же усл.

Пр. Студ. Сдают экз.»С какой вер-ю студ.стоящий первый в списке сдаст экз.с первого раза»

Несовместные и совместные события. Сумма событий. Теорема сложения вероятностей (с доказательством). Пример.

Операция сложения событий. Опр.: Суммой А+В событий А и В назыв. такое со-бытие, которое считается наступившим, если наступило или событие А или В или вместе. Пр.: Извлечение карты: А- извлечен туз; В- извлечены бубны. а)Пусть рез-т: извлечена 7-ка бубен. А+В –наступило. б)Пусть рез-т: извлечен король крестей => А+В –не наступило.А+`А = Е Теоремы сложения вероятностей. Общая формула: P(A+B)=P(A)+P(B)-P(AB).; В частности: Пусть А и В не совместимы, тогда А×В=Æ ; P(AB)=P(Æ)=0 ,т.е. имеем: Теорема: Вероятность суммы двух несовместимых событий = сумме их вероятно-стей., т.е. P(A+B)=P(A)+P(B). 1)Следствие: Пусть события А1,А2,…Ак образуют полную систему, тогда Р(А1)+…+Р(Ак)=1. Док-во: В частности события А1,А2,…Ак –единственно возможны (т.к.)полная сист.), т.е. А1+…+Аn=Е => Р(А1+…+Ак)=Р(Е). По теор. слож. вер-тей: Р(А1)+…+Р(Ак)=1.II.Следствие: Если А и `А –пара противоположных событий, то Р(А)+Р(`А )=1.

Событие наз-ся несовместным, если наступ-ие одного из них исключает наступление какого любого другого.совместные- наоборот.

Полная группа событий. Противоположные события. Соотношение между вероятностями противоположных событий (с выводом). Примеры.

Несколько соб-й образуют полную группу, если она явл.единственно возможными и несовместимыми исходами испытаний . Т.е.в результате испытания обязательно должно произойти одно и только одно из этих событий.

Частым случаем соб-й, образующих полную группу, явл.противоположные события. Два несовместных события, из которых одно должно обязательно произойти, называются противоположные.

Например. «выпадение герба» «решки».

Сумма ве-й противопол.событий равна 1.следует из того что противополож.соб-я образуют полную группу.

Зависимые и независимые события. Произведение событий. Понятие условной вероятности. Теорема умножения вероятностей (с доказательством). Примеры.

Два соб-я называются незавсисимыми, если появление одного изних не меняет вер-ти появление другого.

Теорема Умножения вероятностей.

Т. ~Р(АВ)=Р(А)Ра(В) ~Р(АВС)=Р(А)Ра(В)Рав(С). Следствие. А и В независимы ó

Р(АВ)=Р(А)Р(В), т.е. в частности вер-ть произведений 2-х независимых событий равна произведению их вер-стей. Теорема для независимых вер-тей.=> Р(В1)Р(`В2)+Р(`В1)Р(В2). Пр.: Два стрелка одновременно выстреливают в мишень.Вер-ть попадания для 1-го =0,6; для 2-го 0,8.; Найти: А)Вер-ть того что в мишени будет 1 пробоина. В)будет хотя бы одна пробоина. Реш.: В мишени будет 1 пробо-ина т.ит.т.к. 1-ый попал и 2-ой промахнулся, 1-ый промахнулся и 2-ой попал. А=(В1`В2+`В1В2)=Р(В1`В2)+Р(`В1В2). Используем терему для независ. вер-тей. Р(В1)=0,6; Р(`В1)=1-0,6=0,4; Р(В2)=0,8; Р(`В2)=0,2.; Р(А)=0,6×0,2+0,4×0,8=0,44. ХОТЯБЫ 1 => Р(с)=Р(А+D) {D-2-е попадание} P(D)=P(B1×B2)=P(B1)P(B2)==0,6×0,8=0,48.; P(c)=0,92.

Формулы полной вероятности и Байеса (с доказательством). Примеры.

Т.Пусть соб-я А1,А2..Аn образ-т полную группу соб-й, тогда вер-ть события F равна сумме произведений вер-ти каждого из этих событий на сообтветствующую условную вероятность F.

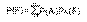
Док-во.

F=A₁F+A₂F+A₃F+…+A_nF

Соб-е A_iF и AjF несовм. (i≠j)

По теор.+вер-ей

P(F)=P(A₁F+..+A_nF)=P(A₁F)+..+P(A_nF)=PA₁)P_A1(F)+..P(A_n)P_An(F)=Σⁿ_i=1P(A_i)P_Ai(F) (т.к.P(A_jF)=P(A_i)P_Ai(F))

Следствие.

Т.(ф-ла Байеса)

Пусть А1,,Аn обр-ют полную группу событий и P(F)≠0

Тогда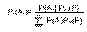

P(AkF)=P(A_k)P_ak(F)=P(F)P_f(A_k)

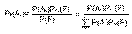
Пр.Имеются 10 карточек

О
В
Л

Наудачу выбираем карточки

Р(ВОЛ)=2/10*4/9*3/8=1/30

Повторные независимые испытания. Формула Бернулли (с выводом). Примеры.

Если вер-ь наступления соб-я А в каждом испытании не меняется в зависимости от исходов других, то в такия испытания наз-ся независимыми относительно соб-я А

Т.Если вер-ть р наступления соб-я А в каждом исп-ии постоянна, то вер-ть P_m,n того,что соб-е А наступит m раз в независимых испытаниях,равна

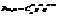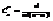где q=1-p

Д-во.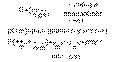

Если + и- помен.местами,товер-ть не измен.,т.е.все элементарные исходы входящие в событие X=m имеют одну и туже вер-ть

Ко-во таких элем.исходов C^m_n (из n элементов выбираются которые с +,порядок выборки не важен)т.е.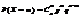

Локальная теорема Муавра—Лапласа, условия ее применимости. Свойства функции f(x). Пример.

Т. Если вер-ть р наступления соб-я А в каждом испы-и постоянна и отлична от 0 и 1, то P_m,n того,что соб-е А наступит m раз в n независ.исыт-ях при достаточно большом числе n,приблиз.=: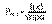

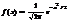ф-я Гаусса

Где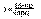

Чем больше n тем точнее вычесл.по ф-л.

причем. 1)число испытаний достаточно велико 2)npq³20, где q=1-р

Свойства функции Гаусса: 1)Четность f(-x)=f(x); 2)Не отрицательность f(x)>0; 3)

lim f(x)=lim f(x)=0 {при хà¥}; Практическое правило: если х³5,то будем полагать, что f(x)»0. {Далее следует график y=f(x) в виде «горки»}