Вычисление числовых характеристик важных распределений.

Вычислим математическое ожидание и дисперсию для наиболее важных распределений.

Название распределения	Математическое ожидание	Дисперсия
Вырожденное в точке a	a
Биномиальное (n,p)
Геометрическое p
Пуассоновское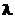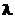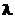
Нормальное стандартное
Нормальное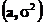
Равномерное на отрезке (0,1)	1/2	1/12
Равномерное на отрезке (A,B)
Бета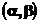
Экспоненциальное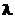
Гамма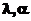

Если случайные величины имеют многомерное нормальное распределение

то

Вычисление всех характеристик представляет собой, по существу, упражнения из математического анализа по суммированию рядов и взятию интегралов. Упростить в ряде случаев эти вычисления можно, если представить исследуемую случайную величину в виде суммы независимых случайных величин и воспользоваться свойствами математического ожидания и дисперсии.

Абсолютная непрерывность вероятностных мер

Понятие абсолютной непрерывности вероятностных мер и распределений играет важную роль в современной теории вероятностей, математической статистике и теории случайных процессов. Дело в том, что для вероятностей, заданных в произвольных вероятностных пространствах, нельзя определить характеристику аналогичную функции распределения, но можно определить характеристику аналогичную плотности распределения. Для того, чтобы это корректно сделать, требуется понятие абсолютной непрерывности одной вероятностной меры относительно другой.

Абсолютно непрерывные и сингулярные меры и распределения

Определение абсолютной непрерывности двух мер.

Пусть - две меры, заданные на одном измеримом пространстве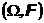

Мера называется абсолютно непрерывной относительно меры , если из того, что для некоторого множества A

, следует что

Обозначается это так

Определение эквивиалентности двух мер.

Меры называются эквививалентными, если и

Обозначается это так

Определение сингулярности двух мер.

Меры называются сингулярными , если существует множество A такое, что и .

Обозначается это так

Следующая теорема, доказательство которой проводится в курсе функционального анализа, поясняет важность понятия абсолютной непрерывности

Теорема Радона-Никодима

Теорема.

Пусть - две сигма-конечные меры и . Тогда существует и единственна с точностью до значений на множестве меры нуль функция такая, что

Единнственность с точностью до значений на множестве меры нуль означает, что если - другая функция, удовлетворяющая условию

, то

Случайная величина называется производной Радона-Никодима меры относительно меры или плотностью меры относительно меры и обозначается так

Если мера абсолютно непрерывна относительно меры , то можно заменять вычисление интеграла Лебега по мере на вычисление интеграла Лебега по мере , что показывает следующая лемма

Лемма.

Пусть - две сигма-конечные меры и . Тогда для любой случайной величины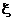

Доказательство.

Для простых случайных величин равенство очевидно. Далее применяем теорему о монотонной сходимости.

Используя данную лемму, нетрудно показать, что если , то

и если - три сигма-конечные меры и , то

Приведем примеры абсолютно непрерывных, эквивалентных и сингулярных распределений и вычислим соответствующие плотности.

Пример 1.

Пусть -два дискретных распределения на одном и том же множестве значений

Тогда , если , то и для тех 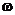, для которых

для остальных 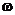можно определять плотность произвольным образом.

Если , то

В частности, любые два пуассоновских распределения эквивалентны, так как для распределения Пуассона величина

положительна при любых

Пример 2.

Пусть -два распределения на прямой с плотностями

Здесь 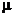- мера Лебега.

Напомним, что плотности определяются неоднозначно

Тогда , если существуют варианты плотностей такие, что , то и для тех , для которых

для остальных можно определять плотность произвольным образом.

Указание: покажите, что если на множестве Aи , то

Доказательство проведите самостоятельно.

В частности, если , то

Например, любые два нормальных распределения эквивалентны, так как для любого нормального распределения существует вариант плотности, который всюду больше нуля.

Пример 3.

Проверьте!

Равномерное распределение на отрезке абсолютно непрерывно относительно равномерного распределения на отрезке , если . Эти распределения эквивалентны тогда и только тогда , когда отрезки совпадают, и сингулярны когда отрезки не пересекаются.