Равномерное распределение на отрезке – мера Лебега.
Рассмотрим следующую функцию распределения
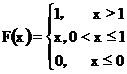
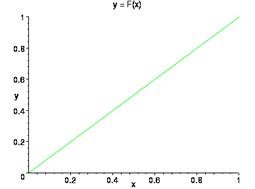
Какими свойствами обладает вероятность, соответствующая этой функции распределения?
Нетрудно увидеть, что вероятность отрезка, целиком лежащего внутри отрезка [0,1], равна его длине.
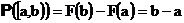
В общем случае для любого отрезка
его вероятность равна длине его пересечения с отрезком [0,1]
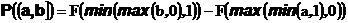
Вероятность одноточечного множества равна нулю.
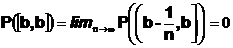
Такая вероятностная мера называется мера Лебега на отрезке [0,1] или равномерное распределение на отрезке [0,1].
Равномерное распределение применяется в тех случаях, когда исход опыта – абсолютно случайная точка отрезка [0,1], например, случайный момент времени. Во многих языках программирования есть функция, возвращающая случайное число из отрезка [0,1] (rand(), random() и т.п. ) – датчик случайных чисел. Используя равномерное распределение, можно моделировать другие распределения, например, бернуллиевское. Действительно, если
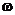
равномерно распределена на отрезке [0,1], то
случайная величина
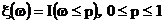
имеет
бернуллиевское распределение с параметром p.
Рассмотрим следующую функцию распределения
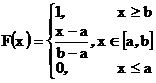
Покажите, что если 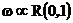 , то , то 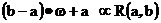 . Нарисуйте график соответствующей функции распределения. . Нарисуйте график соответствующей функции распределения. | эта функция распределения называется функция распределения равномерного распределения на отрезке [a,b]. Случайная величина, имеющая равномерное распределение на отрезке [a,b], называется равномерно распределенная на отрезке [a,b] случайная величина. Для равномерного распределения используют обозначение 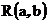 . . |
Мера Лебега на прямой.
Можно показать, что существует (не вероятностная) мера на прямой, которая приписывает каждому отрезку его длину. Эта мера называется мера Лебега (на прямой). В дальнейшем будем обозначать эту меру
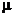
Плотность распределения
В тех случаях, когда функцию распределения можно представить в виде интеграла (Римана) от неотрицательной функции
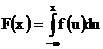
функцию f называют плотностью, соответствующей функции распределения F, или плотностью F .
Если функция распределения имеет плотность, то эта функция распределения непрерывна и такие функции распределения называют абсолютно непрерывными. Точные смысл понятию абсолютная непрерывность будет дан в дальнейшем. Заметим, что представление функции распределения в виде интеграла от некоторой функции неоднозначно, поэтому у одной функции распределения может быть несколько различных плотностей. Впрочем, различаться они могут только в не очень большом числе точек. Поэтому обычно плотностью называют наиболее прилично ведущую себя функцию f – непрерывную или почти непрерывную. Ее и приводят в различных справочниках. Нарисуем, например, график плотности равномерного на отрезке [0,2] распределения.
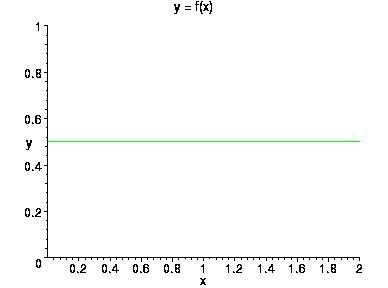
Очевидно, любая плотность удовлетворяет условию
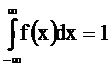
Зная плотность распределения нетрудно подсчитывать вероятности различных множеств.
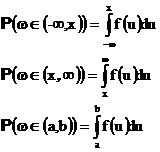
и, вообще, если индикаторная функция
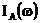
множества
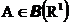
интегрируема по Риману на любом конечном отрезке, то
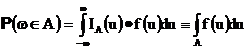
Если g(x) – неотрицательная функция, удовлетворяющая условию
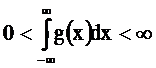
то функция
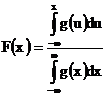
будет функцией распределения с плотностью
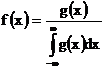
Этот факт позволяет построить множество примеров непрерывных функций распределения
