Отображения вероятностных пространств

Дадим формальное определение отображения вероятностного пространства в измеримое пространство

Пусть

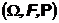
основное вероятностное пространство

измеримое пространство

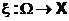
поточечное отображение (функция), ставящее в соответствие каждому элементарному исходу основного пространства точку x пространства X.

Отображение

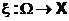
называется измеримое отображение, если

множество (прообраз B)

Покажите, что так определенная функция будет вероятностью

Измеримость отображения гарантирует, что функция

определенная на сигма-алгебре

по формуле

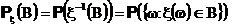
будет вероятностью.

Эта функция называется распределение, индуцированное отображением

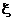
или просто распределение

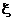
Таким образом с каждым отображением

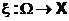
связано новое вероятностное пространство

.

Докажите это!

Заметим также, что совокупность прообразов всех множеств из Bобразует сигма-алгебру, которая обозначается и называется сигма-алгебра, порожденная отображением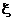

Мы часто будем пользоваться отображениями пространств, так как каждое такое отображение указывает связь между различными математическими моделями.

Случайная величина

Случайной величиной называется измеримое отображение основного вероятностного пространства в множество действительных чисел. С практической точки зрения случайная величина это числовая характеристика эксперимента. Чтобы дать корректное определение случайной величины, необходимо указать подходящую сигма-алгебру на пространстве действительных чисел. В дальнейшем пространство действительных чисел будем обозначать

а пространство векторов с n действительными координатами

Борелевская сигма-алгебра

Так как сигма-алгебра на пространстве действительных чисел нужна нам для того, чтобы определить на ней вероятность, то естественно включить в эту сигма-алгебру побольше практически важных множеств. Обозначим

минимальную сигма-алгебру, содержащую всевозможные интервалы вида

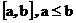
Эта сигма-алгебра называется борелевская сигма-алгебра (Борель Эмиль). Она содержит все практически важные множества действительной прямой. Множество, принадлежащее борелевской сигма-алгебре называется борелевское множество.

Точка

Очевидно, что любая точка это замкнутый интервал с одинаковыми концами

Открытый интервал

Покажем, что любой открытый интервал содержится в борелевской сигма- алгебре. Действительно, из определения сигма-алгебры следует, что вместе с каждой парой множеств A, B сигма-алгебра содержит пересечение, объединение и, следовательно, разность этих множеств.

Осталось заметить,что

Полуось