Расчет надежности сложной системы.

Если сложную систему удается представить в виде последовательно-параллельного соединения элементов, то ее надежность можно рассчитать последовательно рассчитывая надежности ее частей и заменяя каждую часть элементов одним элементом.

На рисунке приведене пример такой системы. На элементах указаны вероятности их отказа.

Заменим три последовательно соединенных верхних элемента одним, с вероятностью отказа 0,352 = 1-(1-0,1)*(1-0,2)*(1-0,1), а два параллельных внизу одним с вероятностью отказа 0,09=0,3*0,3. Тогда получим следующую схему

Заменяя сначала последовательно соединенные элементы одним с вероятностью отказа 0,0991=1 - (1-0,09)*(1-0,01), затем получившиеся параллельно соединенные элементы одним с вероятностью 0,0348832 =0,352 * 0,0991 получим

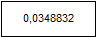
Таким образом вероятность безоказной работы системы равна 1-0,0348832 =0,9651168.

Замечания к примерам.

1. В предыдущих примерах элементарный исход представлял собой вектор, координаты которого были однородны – принимали значения из одного и того же множества. Нет никаких ограничений при построении вероятностных пространств с использованием понятия независимости для объединения разнородных опытов – например бросания несимметричной монеты и симметричной игральной кости одновременно. В этом случае первая координата имеет два значения (1 – герб) , вторая - шесть и

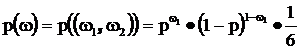
Здесь p – вероятность выпадения герба.

2. Замена параллельно или последовательно соединенных элементов одним является частным случаем т.н. отображения вероятностных пространств. Действительно, для расчета вероятностей отказа нам пришлось описать исходную систему с n элементами элементарным исходом с n двоичными координатами ( по числу элементов). При этом число возможных состояний системы равно

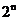
С другой стороны с точки зрения надежности система может находится только в двух состояниях – исправна или неисправна (отказ). Поэтому для описания надежности системы достаточно двух элементарных исходов – 0,1. Еще раз заметим, что один опыт, с разной степенью детальности может быть описан разными пространствами элементарных исходов.

Каждому элементарному исходу (состояниям элементов) в первом пространстве соответствует либо 0 (отказ системы) либо 1 (исправность системы) во втором пространстве.

Таким образом мы имеем два вероятностных пространства, основное

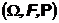
на котором мы задали вероятность с использованием детальных представлений об опыте и второе (пространство значений)

,

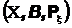
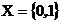B –наибольшая сигма-алгебра.

Во втором пространстве мы определили вероятность с помощью отображения (функции )

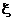
которая каждому элементарному исходу первого опыта ставит в соответствие элементарный исход второго опыта.

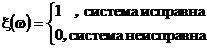
Замена сложной системы одним элементом равносильна указанному отображению пространств. Вероятность на втором пространстве не определяется независимо, а вычисляется с использованием вероятности, заданной на основном пространстве и отображения

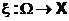
Если изменить вероятность на основном пространстве или отображение, то изменится и вероятность на пространстве значений. Например, при изменении надежности отдельных элементов изменится вероятность P,при изменении схемы соединения – отображение.

Для того чтобы отметить зависимость вероятности на пространстве значении от основной вероятности и отображения ее обозначают

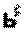
например

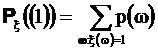
Условная вероятность

Часто случайные компоненты в опыте и соответственно координаты элементарного исхода являются зависимыми. В этом случае для определения распределения используют понятие условной вероятности.

Урновая схема

Рассмотрим, например, эксперимент, описывающий выбор двух шаров из урны, содержащей 20 черных и 10 белых шаров, без возвращения. Элементарным исходом будет вектор

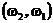
из нулей и единиц (1 – черный шар, 0 - белый), где первая координата описывает цвет второго извлеченного шара, а вторая цвет первого извлеченного шара.

Как задать вероятность элементарного исхода?

Ясно, что событие «На первом шаге вынут черный шар» должно иметь вероятность

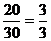
Ясно также, что если бы мы знали цвет извлеченного на первом шаге шара, то точно также могли бы определить вероятность извлечения черного шара на втором шаге. Именно, если первый шар белый, то (при этом условии) вероятность извлечь черный шар на втором шаге равна

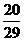
Если первый шар черный, то

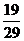
Тогда естественно определить вероятность исхода (1,1) так чтобы выполнялась формула условной вероятности

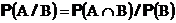
т.е.

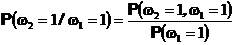
и

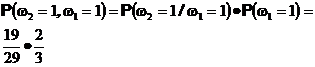
Аналогично определяются вероятности остальных элементарных исходов

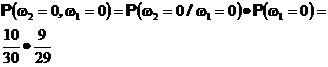
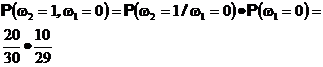
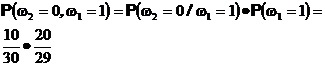
Теперь нетрудно, например, вычислить вероятность того, что второй извлеченный шар будет черным. Она равна

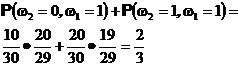
Покажите, что нас самом деле вероятность вытащить черный шар одинакова не только для первого и второго, но и для любого другого шага выбора (пока она не станет равной, естественно, нулю – когда кончатся черные шары)

Заметим, что данный результат в применении к задаче о студенте на экзамене означает, что студенту все равно каким идти – первым или вторым.

Марковская зависимость

Легко распространить изложенное выше на случай элементарного исхода с n целочисленными координатами.

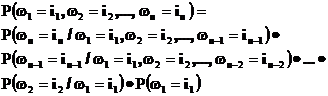
Особенно просто записывается вероятность элементарного исхода когда имеет место марковская зависимость координат, т.е. когда распределение следующей координаты зависит только от значения предыдущей координаты

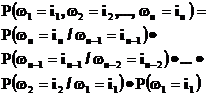
В этом случае последовательные переходы от координаты 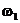к координате 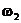и т.д. называются шагами ,а вероятности

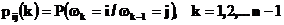
называются переходными вероятностями (за один шаг).

Если каждая координата вектора 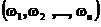принимает значения в одном и том же конечном множестве 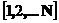(множестве состояний) и переходные вероятности не зависят от n,топоследовательность 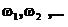называется конечной цепью Маркова. В этом случае вероятность элементарного исхода можно записать так

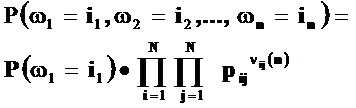
где

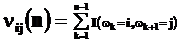
- количество переходов из состояния i в состояние j

Подробно марковские зависимости исследуются в теории случайных процессов.