Расчет на устойчивость прямых сжатых стержней

Потеря устойчивости сжатого прямолинейного стержня будет сопровождаться его изгибом.

Наименьшая критическая сила называется первой критической или эйлеровой силой:

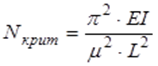
где μ – коэффициент, зависящий от условий опирания стержня.

При значениях продольной сжимающей силы меньше критического значения (N<N_крит) прямолинейная форма равновесия центрально сжатого стержня является устойчивой.

При значениях продольной сжимающей силы больше критического значения (N>N_крит) прямолинейная форма равновесия центрально сжатого стержня является неустойчивой.

Таблица значений критической силой для различных схем стержней

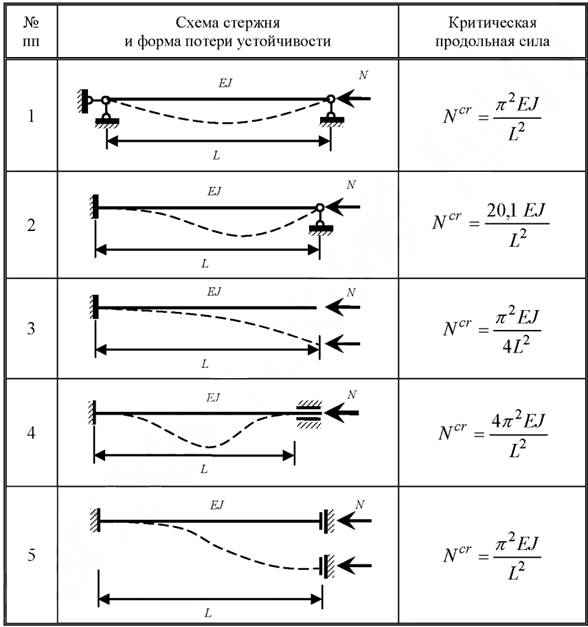
Таблица значений критической силой для различных схем стержней

С. Задача 1

Необходимо определить критическую величину внешней нагрузки.

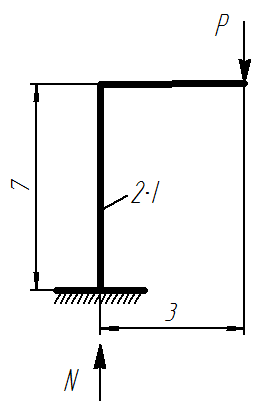
Устойчивость сжатого стержня

Критическая сила для данной схемы определяется по формуле:

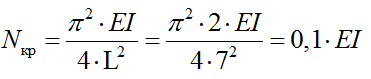
Определяем зависимость критической сжимающей силы от внешней нагрузки:

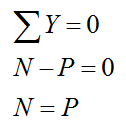
Определяем критическое значение внешней нагрузки:

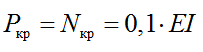
С. Задача 2

Необходимо определить критическую величину внешней нагрузки.

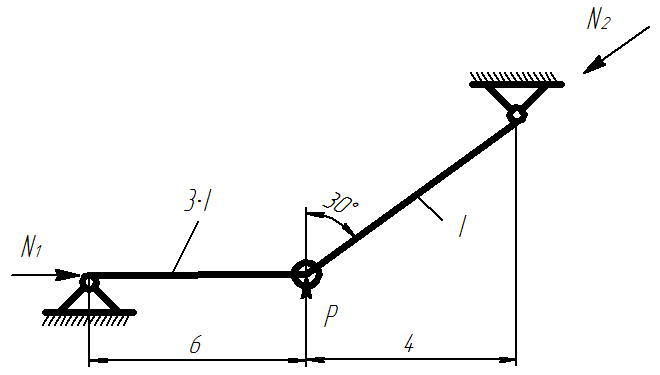
Устойчивость сжатых стержней

Потерять устойчивость может как первая, так и вторая балки, соединенные шарниром. Таким образом, необходимо определить критические значения сил N₁ и N₂ и выбрать для всей системы наименьшее значение.

Критические силы для данной схемы определяются по формулам:

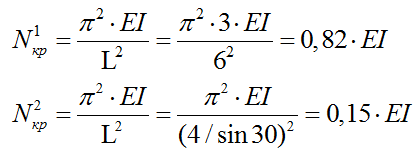
Определяем зависимость критических сжимающих сил от внешней нагрузки:

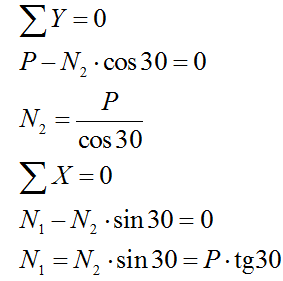
Определяем критическое значение внешней нагрузки:

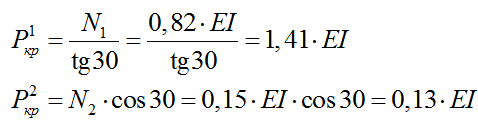
Принимаем минимальное значение из двух критических значений сил:

Критическая величина внешней нагрузки:

Расчет на устойчивость статически неопределимой рамы

Моменту потери устойчивости системы соответствует неравенство нулю неизвестных перемещений, т.е. определитель матрицы, составленной из главных и боковых коэффициентов системы канонических уравнений метода перемещений, должен быть равен нулю:

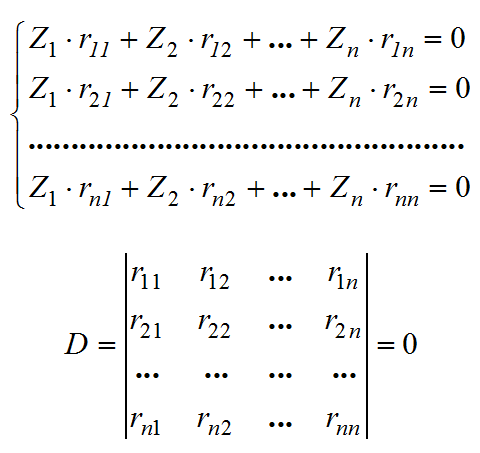
Раскрытие определителя приводит к уравнению, называемому уравнением устойчивости. Наименьшая из нагрузок, удовлетворяющая данному уравнению, называется критической нагрузкой.

Критическая сила определяется по формуле:

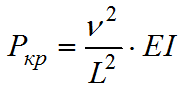
где ν – критический параметр;

L – длина балки, которую сжимает внешняя сила, м;

EI – изгибная жесткость.

Для стержней, которые сжимает внешняя сила, необходимо определить погонную жесткость:

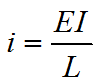
Сжимающая сила, действующая на стержень, приводит к тому, что эпюра изгибающих моментов на данном стержне приобретает криволинейный вид. Ниже приведена таблица 1 для метода перемещений эпюр изгибающих моментов для различных схем стержней с учетом сжимающей силы, являющаяся дополнением к таблице эпюр изгибающих моментов метода перемещений.

Таблица 1. Эпюры изгибающих моментов метода перемещений

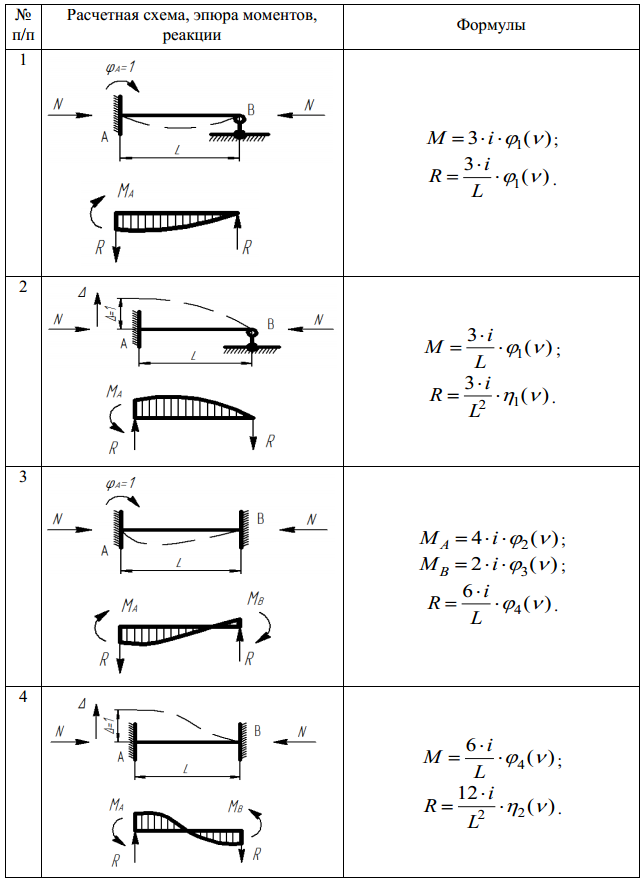
Таблица эпюр изгибающих моментов метода перемещений

Таблица 2. Критический параметр ν

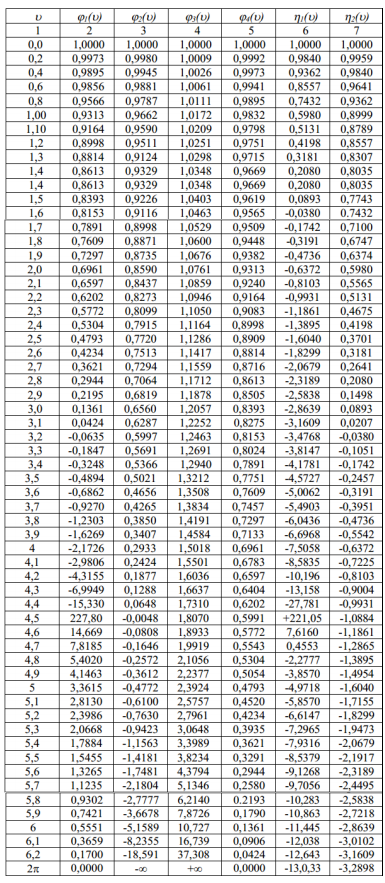Критический параметр

С. Задача 1

Определить значение критической силы, при которой происходит потеря устойчивости статически неопределимой рамы.

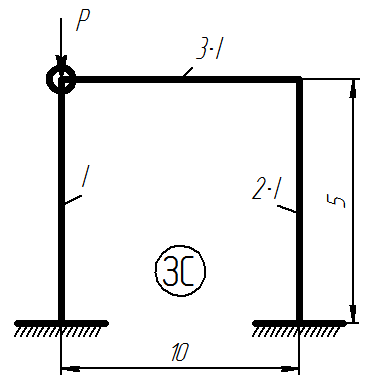
Статически неопределимая рама

1) Определяем степень статической неопределимости системы и строим основную систему как в методе перемещений:

1.1) Определяем степень статической неопределимости системы:

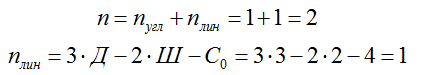
1.2) Выбираем основную систему:

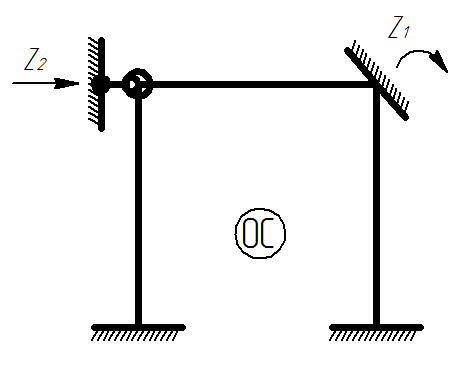
Основная система

2) Определяем погонные жесткости стержней, на которые действует сжимающая внешняя сила:

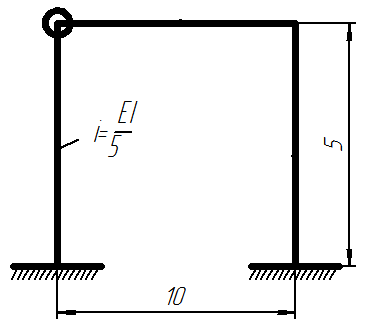
Погонные жесткости

3) Строим эпюры изгибающих моментов от единичных сил по обоим таблицам эпюрметода перемещений:

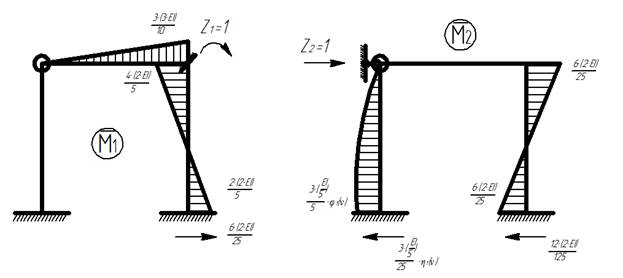
Эпюры изгибающих моментов от единичных сил

4) Определяем главные и боковые коэффициенты:

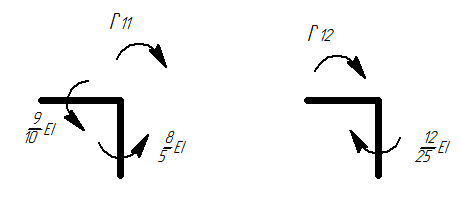
Вырезание узлов

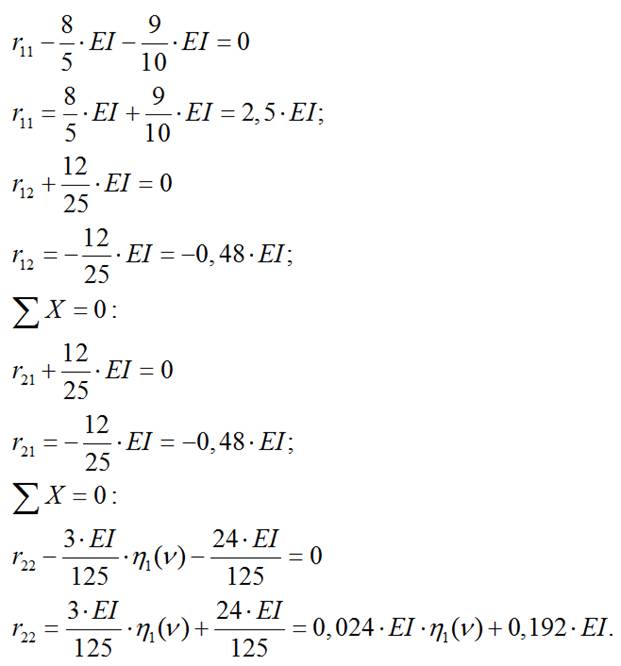
5) Составляем уравнение устойчивости системы и решаем полученное уравнение:

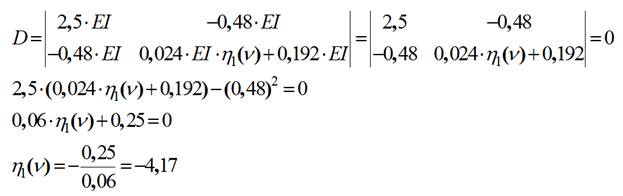
6) По таблице критических параметров определяем критический параметр: ν=3,4.

7) Определяем величину критической силы:

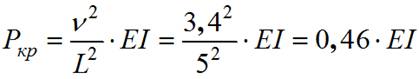
С. Задача 2

Определить значение критической силы, при которой происходит потеря устойчивости статически неопределимой рамы.

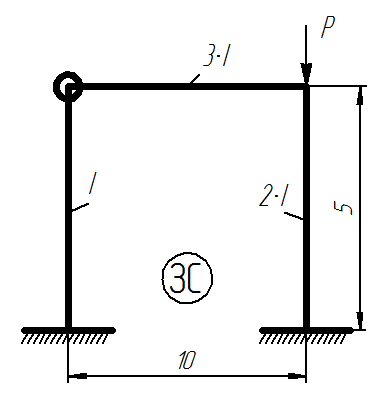
Статически неопределимая рама

1) Определяем степень статической неопределимости системы и строим основную систему как в методе перемещений:

1.1) Определяем степень статической неопределимости системы:

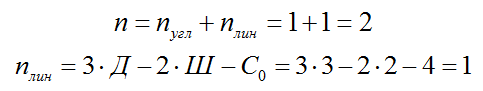
1.2) Выбираем основную систему:

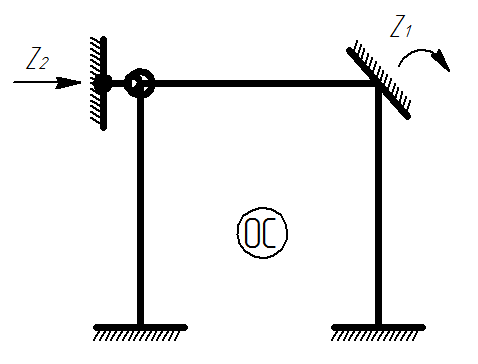
Основная система

2) Погонные жесткости стержней аналогичны задаче 1.

3) Строим эпюры изгибающих моментов от единичных сил:

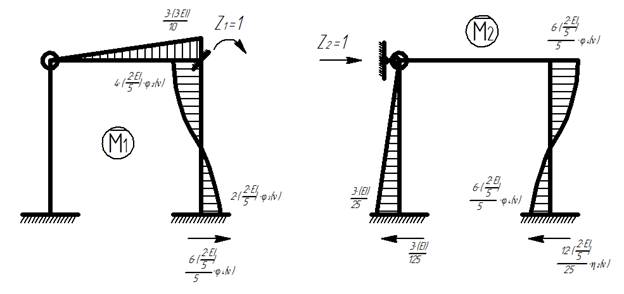
Эпюры изгибающих моментов от единичных сил

4) Определяем главные и боковые коэффициенты:

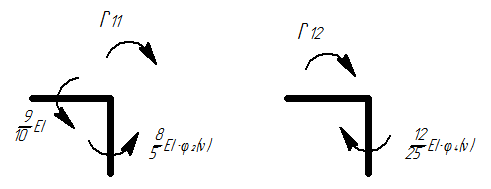
Вырезание узлов

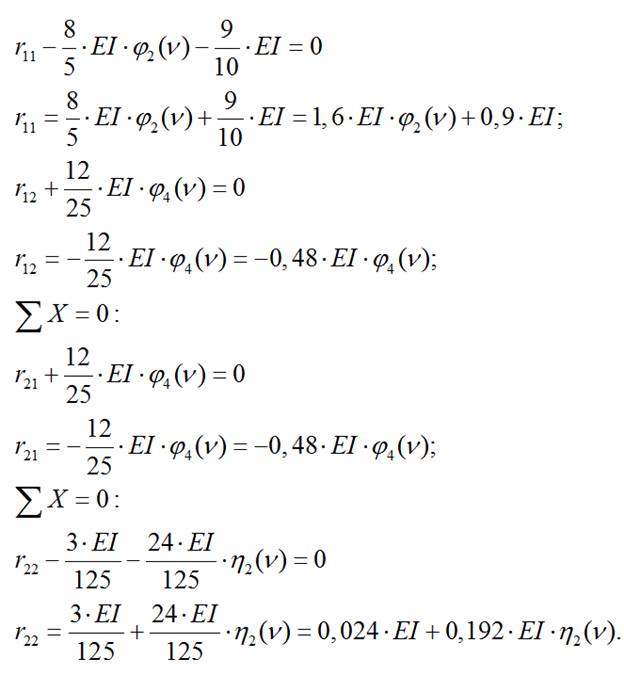
5) Составляем уравнение устойчивости системы:

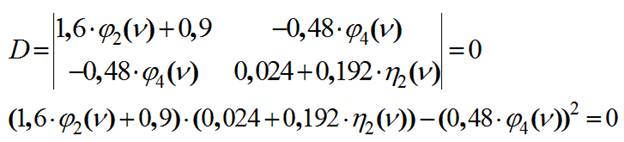
6) Необходимо найти такое значение ν, при котором определитель будет равен нулю. Параметр 0≤ν≤2π.

Задаемся значениями: 2≤ν≤3, между которыми должен находиться искомый критический параметр.

Критический параметр можно определить через подобие треугольников:

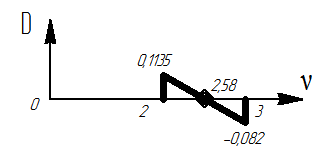
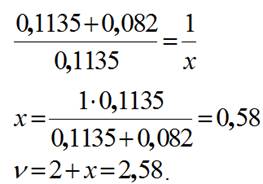
7) Определяем величину критической силы:

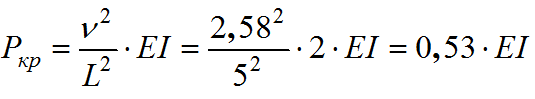
С. Задача 3

Определить значение критической силы, при которой происходит потеря устойчивости статически неопределимой рамы.

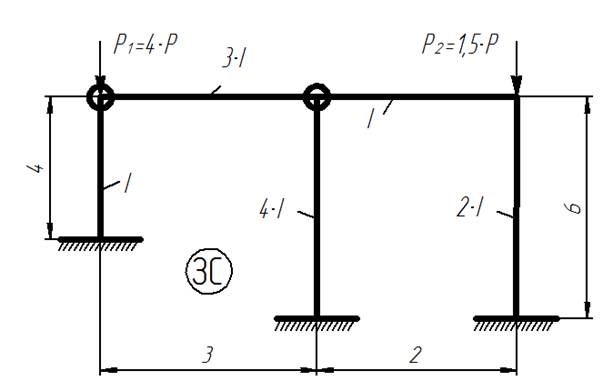
Статически неопределимая рама

1) Определяем степень статической неопределимости системы и строим основную систему как в методе перемещений:

1.1) Определяем степень статической неопределимости системы:

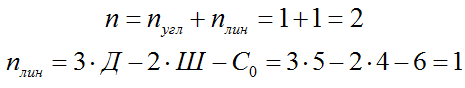
1.2) Выбираем основную систему:

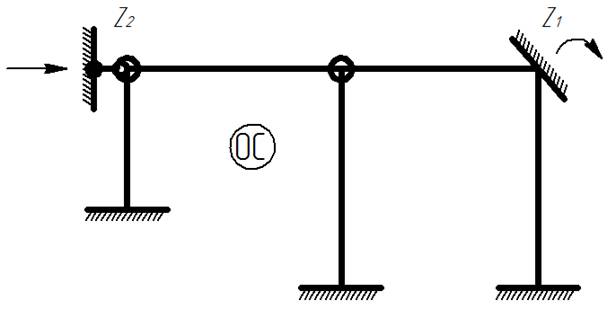
Основная система

2) Определяем погонные жесткости стержней

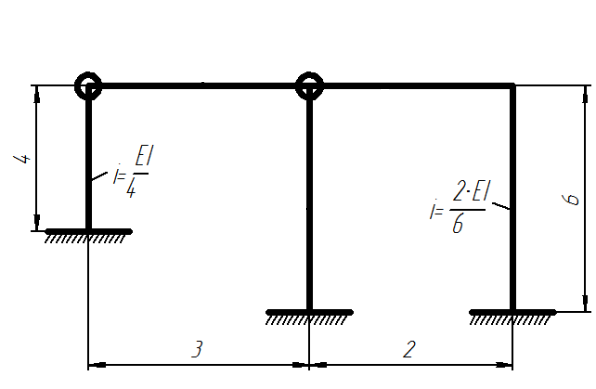
Погонные жесткости стержней

3) Определяем критический параметр для каждой стойки (критические силы для каждой стойки различны):

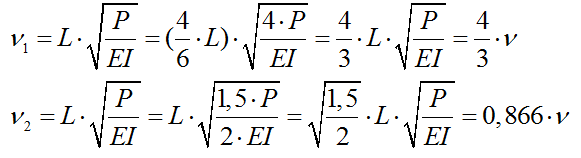
4) Строим эпюры изгибающих моментов от единичных сил:

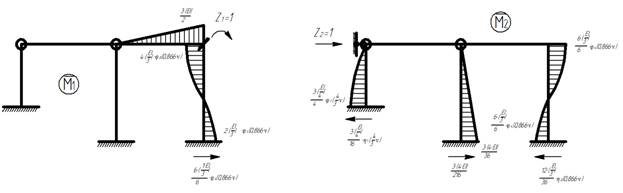
Эпюры изгибающих моментов от единичных сил

5) Определяем главные и боковые коэффициенты:

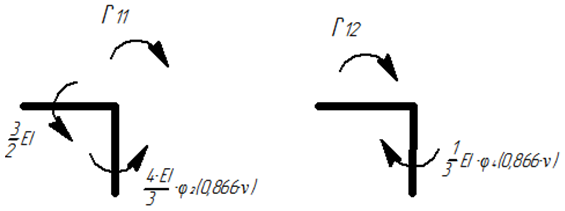
Вырезание узлов

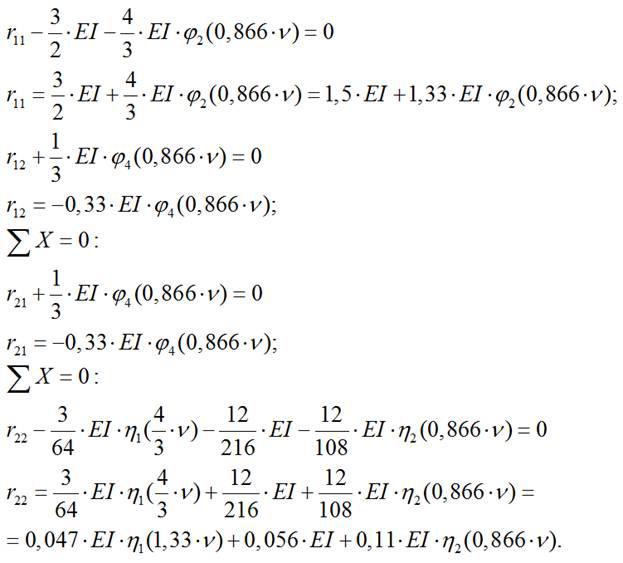
6) Составляем уравнение устойчивости системы:

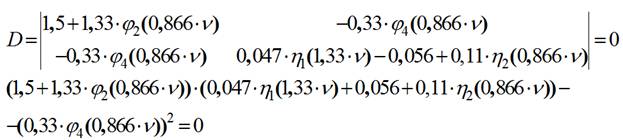
7) Необходимо найти такое значение ν, при котором определитель будет равен нулю. Параметр 0≤ν≤2π.

Задаемся значениями: 1≤ν≤4.

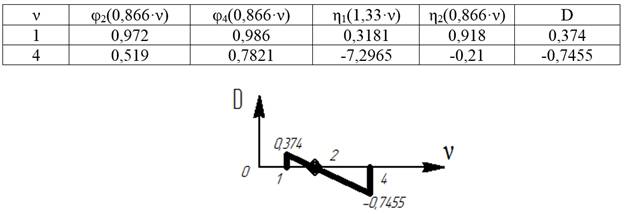
Критический параметр: ν=2.

8) Определяем величину критической силы:

Уравнение трех моментов

Сплошная балка, перекрывающая несколько пролетов, не прерывающаяся шарнирами, называется неразрезной.

Степень статической неопределимости неразрезной балки определяется по формуле:

n=C₀-3

Неразрезную балку обычно решают методом сил. В качестве основной системы выбирают балку с установленными над промежуточными опорами шарнирами. При таком выборе основной системы балка делится на отдельные однопролетные балки.

Если какой-либо конец балки имеет заделку (рис. 1), то в основной системе со стороны этого конца добавляется вместо заделки пролет длиной нуль. Консольные части балки (рис. 2) в основной системе отбрасываются, а их действия заменяются известными моментами.

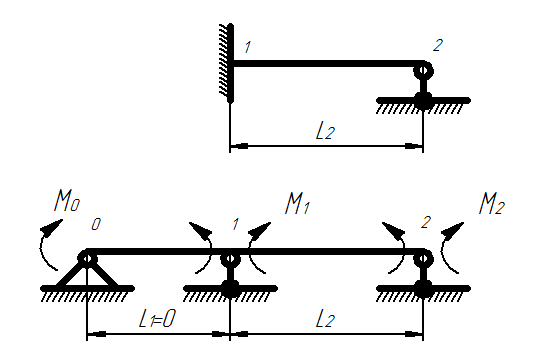Рисунок 1. Неразрезная балка

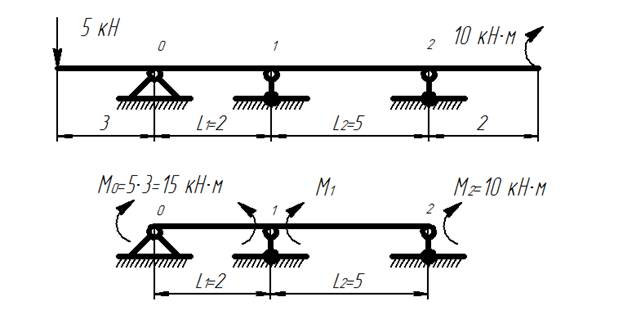
Рисунок 2. Неразрезная балка

Для каждой отдельной балки (участок между установленными шарнирами) строятся эпюры моментов от действия внешних сил, которые на ней расположены.

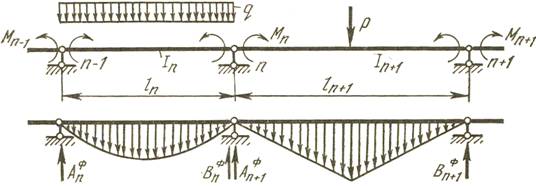
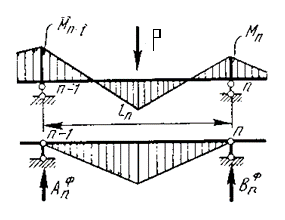
Каноническое уравнение метода сил для балки постоянного сечения принимает вид уравнения трех моментов и содержит не более трех неизвестных:

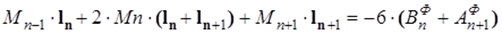
где M_n-1, M_n, M_n+1 – моменты на опорах n-1, n, n+1;

l_n, l_n+1 – длины соответствующих пролетов;

Bn^Ф, An+1^Ф – фиктивные опорные реакции.

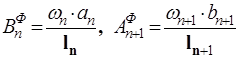
где ω_n, ω_n+1 – площади эпюр моментов для простых балок;

a_n, b_n+1 – расстояние от центра тяжести соответствующей площади фигуры, ограниченной эпюрой моментов, до ближайшей левой опоры n или ближайшей правой опоры n+1.

Составляется столько уравнений трех моментов сколько лишних связей и, решив их, находятся неизвестные опорные моменты.

Строится эпюра опорных моментов М_оп – полученные значения опорных моментовоткладываются от оси и соединяются прямыми в пределах пролетов.

Эпюра М для неразрезной балки равна сумме грузовых эпюр отдельных балок М_р и эпюры опорных моментов М_оп.

Пример задачи с решением.

С. Задача 1

Построить эпюру изгибающих моментов для неразрезной балки с помощью уравнения трех моментов.

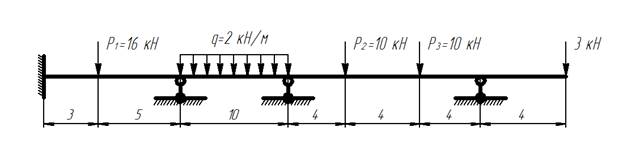
Неразрезная балка

1) Составляется основная система неразрезной балки:

Основная система для способа уравнений трех моментов

2) Строятся эпюры изгибающих моментов для отдельных балок, на которые действуют внешние нагрузки:

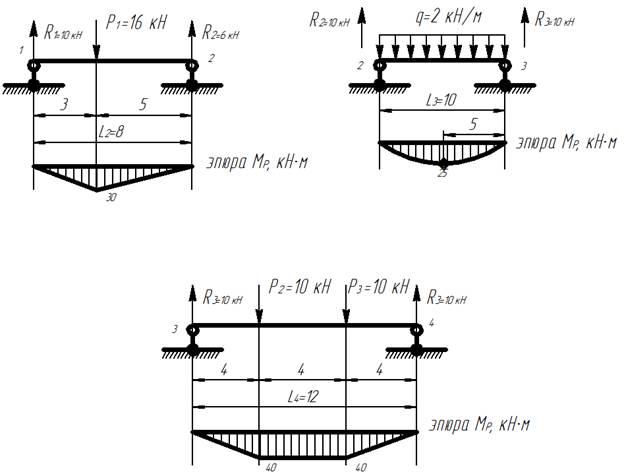
Эпюры изгибающих моментов для отдельных балок

Распишем построение эпюры для пролета L₂:

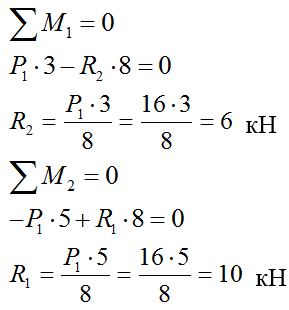
и т.д. для остальных пролетов.

3) Составляются уравнения трех моментов:

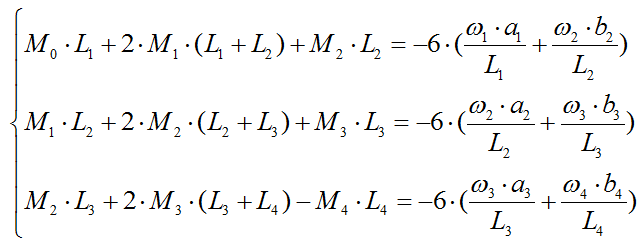
4) Определяются площади и центры тяжести соответствующих эпюр изгибающих моментов простых балок:

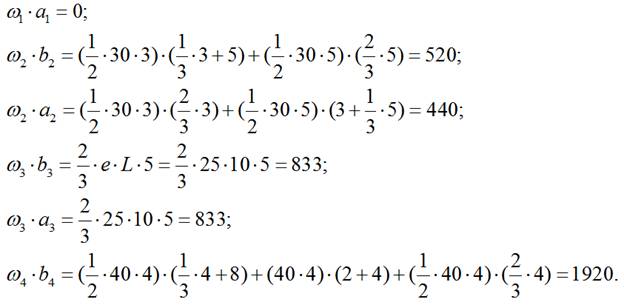
5) Преобразуем уравнения трех моментов:

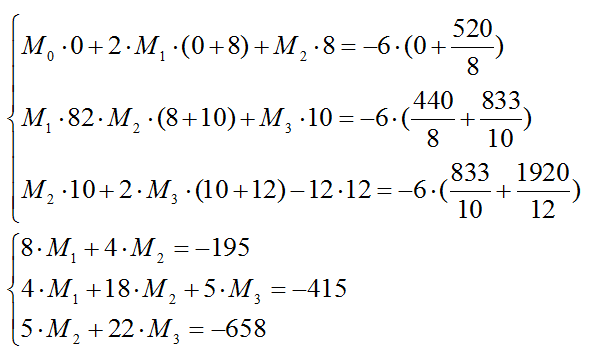
6) Решаем уравнения трех моментов:

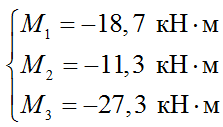
7) Строим эпюру моментов в опорах М_оп.

8) Строим итоговую эпюру моментов М, равную сумме эпюр моментов в опорах М_опи всех эпюр M_р, построенных для отдельных балок.

9) Выполняем проверку. Строим единичную эпюру от действия единичной силы в крайней правой опоре. Если произведение единичной эпюры на итоговую эпюру равно нулю, то расчет выполнен верно.

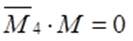
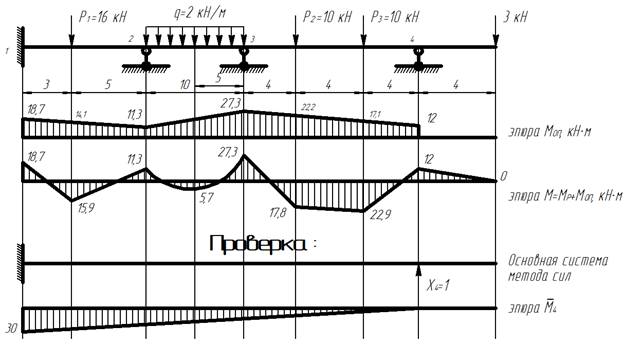
Расчет неразрезной балки с помощью уравнений трех моментов

Метод фокусных отношений

Если пролеты балки загружены постоянной или временной нагрузками, то расчет можно выполнять методом моментных фокусов.

Если на одном из пролетов балки расположить нагрузку, то эпюры изгибающих моментов в незагруженных пролетах балки приобретают вид наклонных прямых с нулевыми ординатами в пределах пролетов. Сечения балок с нулевыми ординатами называются моментными фокусами.

Нулевая точка эпюры изгибающих моментов в пролете при расположении нагрузки справа (слева) от рассматриваемого пролета называется левым (правым) фокусом какого-либо пролета.

Любой пролет балки имеет две (левую и правую) фокусные точки, которые не зависят от нагрузки и занимают определенное положение.

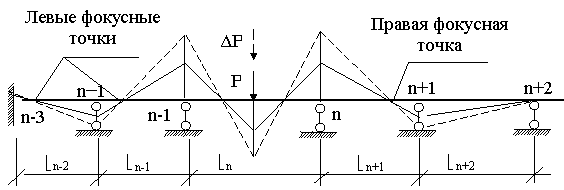
Метод фокусных отношений

Отношение большего опорного изгибающего момента к меньшему в незагруженном пролете называется моментным фокусным отношением.

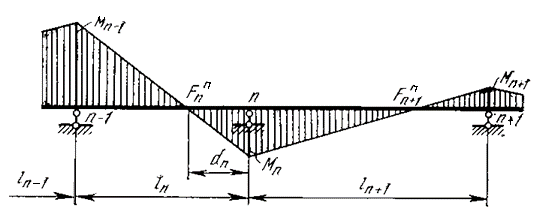
Метод фокусных отношений

Левые фокусные отношения определяются по формуле:

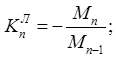
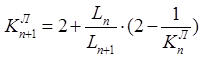
Правые фокусные отношения определяются по формуле:

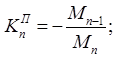
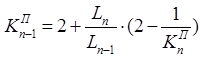
Рассчитываются фокусные отношения всех пролетов. Вначале определяются фокусные отношения крайних пролетов и через них определяют фокусные отношения остальных пролетов по формулам. При шарнирномопирании крайнего пролета фокусное расстояние для него равно бесконечности (∞) (рис. 1, а).

Для пролета с заделкой (она заменяется дополнительным пролетом длиной 0) фокусное отношение в заделке определяется по формуле (рис. 1, б):

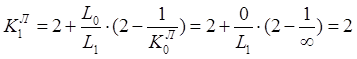
а) б)

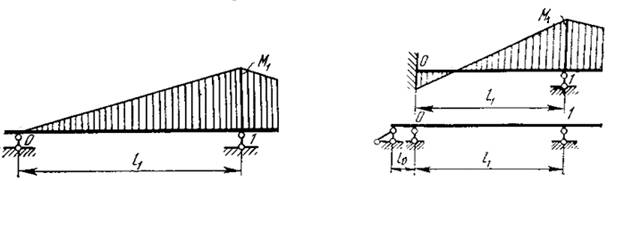
Рисунок 1.Фокусные отношения

Для построения эпюры изгибающих моментов при загрузке одного из пролетов вначале определяются опорные моменты по концам этого пролета по формулам:

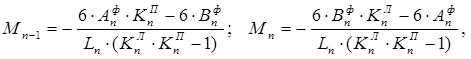
где Bn^Ф, An^Ф – левая и правая фиктивные опоры соответственно.

Метод фокусных отношений

Моменты в остальных пролетах определяются по формулам:

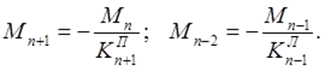
Пример задачи с решением.

С. Задача 2

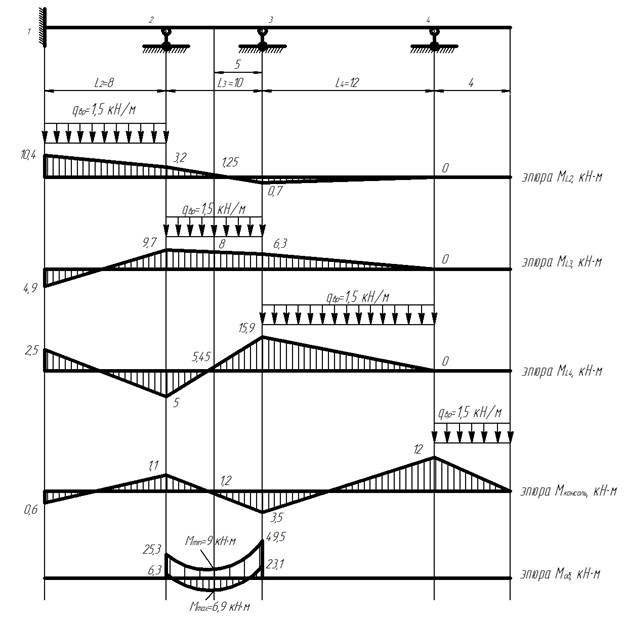
Построим для заданной балки эпюры изгибающих моментов способом фокусных отношений в результате последовательного загружения всех пролетов временной нагрузкой (например, q_вр=1,5 кН/м). Для пролета L₃ построим объемлющую эпюру для точек 2, 3, 0,5·L₃.

По аналогии с методом уравнений трех моментов, если есть заделка, то вместо нее добавляется пролет L=0 (на схеме балке не указан, т.к. схема аналогична задаче для метода трех моментов).

Расчет неразрезной балки способом фокусных отношений

1) Определяем фокусные расстояния (левые и правые):

1.1) левые:

При шарнирном опирании крайнего левого пролета фокусное расстояние для следующего номера опоры равно бесконечности (∞) в соответствии с формулой:

М_n-1 =0, т.к. крайняя опора n-1 является шарнирной, т.е.:

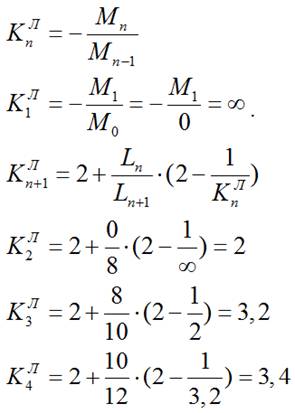
1.2) правые:

При шарнирном опирании крайнего правого пролета фокусное расстояние для номера крайней опоры равно бесконечности (∞) в соответствии с формулой:

М_n =0, т.к. крайняя опора n является шарнирной, т.е.:

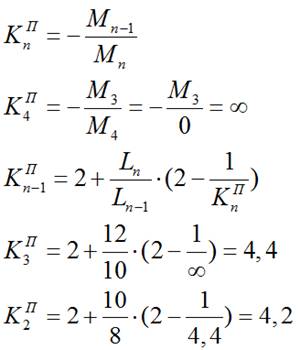
2) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр в пролете L₂:

2.1) Определяем фиктивные опорные реакции от q_{вр (по формуле для способа уравнений трех моментов)}:

Для распределенной нагрузки может применяться следующая формула:

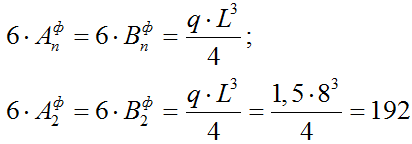
2.2) Определяем моменты в опорах:

Моменты в опорах определяются по формулам:

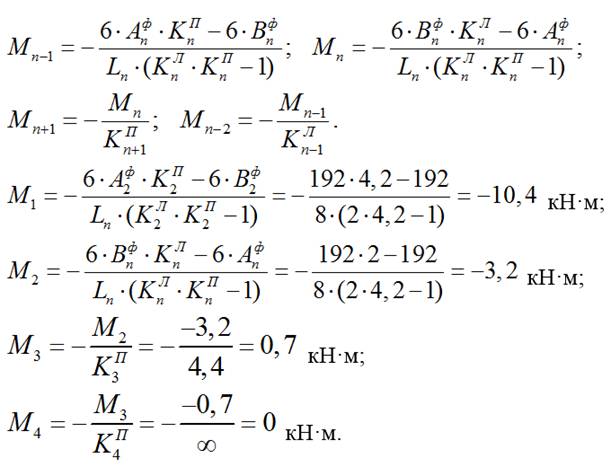
3) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр в пролете L₃:

3.1) Определяем фиктивные опорные реакции от q_вр:

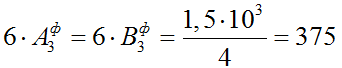
3.2) Определяем моменты в опорах:

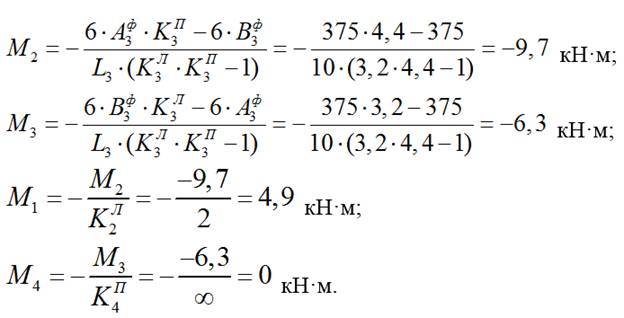
4) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр в пролете L₄:

4.1) Определяем фиктивные опорные реакции от q_вр:

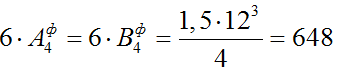
4.2) Определяем моменты в опорах:

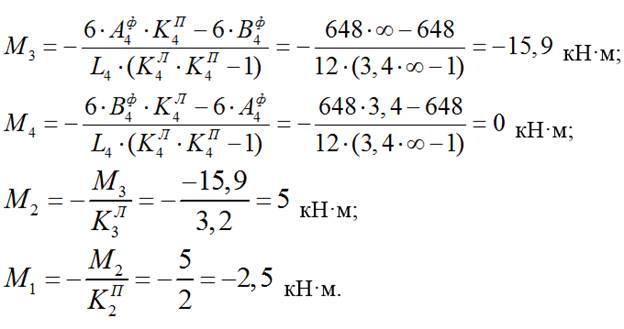
5) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр, действующей на консоли:

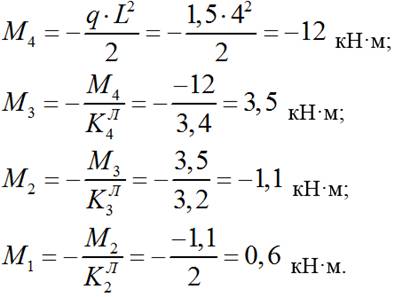
6) Строим объемлющую эпюру для пролета L₃ (точек 2, 3, 0,5·L₃). Она строится при одновременном действии временной нагрузки во всех пролетах и постоянной нагрузки.

Значения эпюры изгибающего момента от действия постоянной нагрузки берем из решения задачи 1 с помощью уравнения трех моментов.

Максимальные значения определяем сложением значений из эпюры изгибающего момента от действия постоянной нагрузки с положительными значениями эпюр изгибающего момента от действия временной нагрузки в рассматриваемых точках.

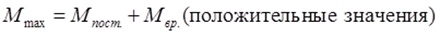
Минимальные значения определяем сложением значений из эпюры изгибающего момента от действия постоянной нагрузки с отрицательными значениями эпюр изгибающего момента от действия временной нагрузки в рассматриваемых точках.

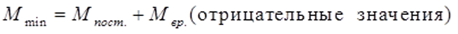
Полученные значения для удобства записи заносим в таблицу 1:

Таблица 1

С. Задача 2

Построим для заданной балки эпюры изгибающих моментов способом фокусных отношений в результате последовательного загружения всех пролетов временной нагрузкой (например, q_вр=1,5 кН/м). Для пролета L₃ построим объемлющую эпюру для точек 2, 3, 0,5·L₃.

По аналогии с методом уравнений трех моментов, если есть заделка, то вместо нее добавляется пролет L=0 (на схеме балке не указан, т.к. схема аналогична задаче для метода трех моментов).

Расчет неразрезной балки способом фокусных отношений

1) Определяем фокусные расстояния (левые и правые):

1.1) левые:

При шарнирном опирании крайнего левого пролета фокусное расстояние для следующего номера опоры равно бесконечности (∞) в соответствии с формулой:

М_n-1 =0, т.к. крайняя опора n-1 является шарнирной, т.е.:

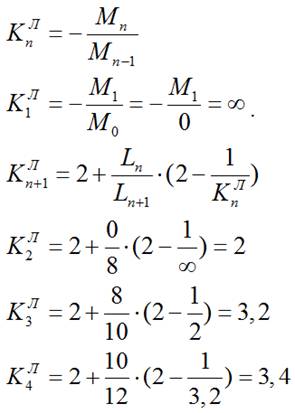
1.2) правые:

При шарнирном опирании крайнего правого пролета фокусное расстояние для номера крайней опоры равно бесконечности (∞) в соответствии с формулой:

М_n =0, т.к. крайняя опора n является шарнирной, т.е.:

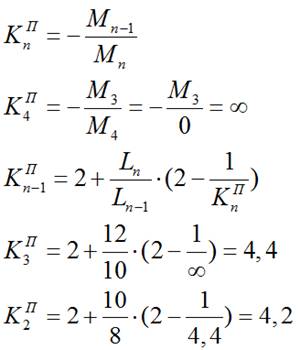
2) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр в пролете L₂:

2.1) Определяем фиктивные опорные реакции от q_{вр (по формуле для способа уравнений трех моментов)}:

Для распределенной нагрузки может применяться следующая формула:

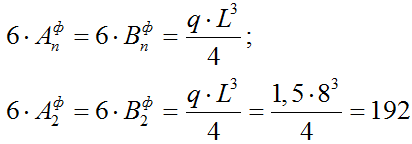
2.2) Определяем моменты в опорах:

Моменты в опорах определяются по формулам:

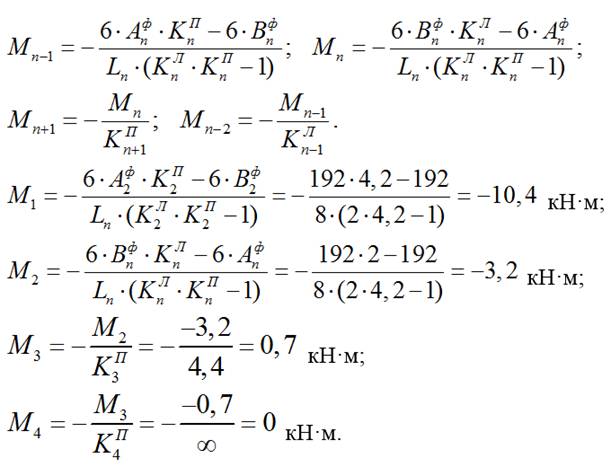
3) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр в пролете L₃:

3.1) Определяем фиктивные опорные реакции от q_вр:

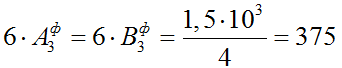
3.2) Определяем моменты в опорах:

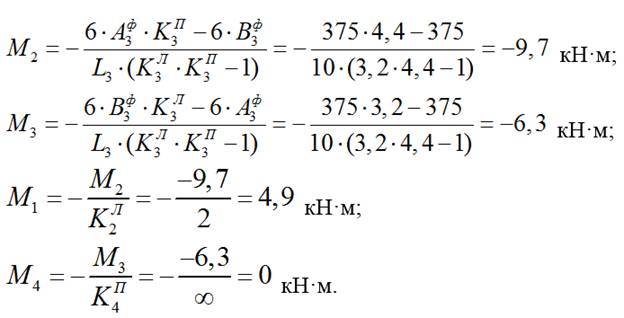
4) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр в пролете L₄:

4.1) Определяем фиктивные опорные реакции от q_вр:

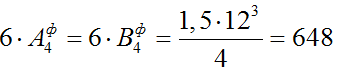
4.2) Определяем моменты в опорах:

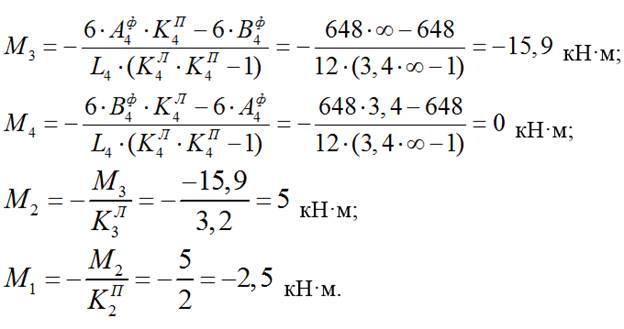
5) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр, действующей на консоли:

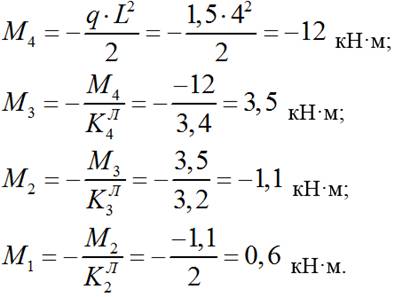
6) Строим объемлющую эпюру для пролета L₃ (точек 2, 3, 0,5·L₃). Она строится при одновременном действии временной нагрузки во всех пролетах и постоянной нагрузки.

Значения эпюры изгибающего момента от действия постоянной нагрузки берем из решения задачи 1 с помощью уравнения трех моментов.

Максимальные значения определяем сложением значений из эпюры изгибающего момента от действия постоянной нагрузки с положительными значениями эпюр изгибающего момента от действия временной нагрузки в рассматриваемых точках.

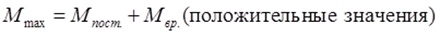
Минимальные значения определяем сложением значений из эпюры изгибающего момента от действия постоянной нагрузки с отрицательными значениями эпюр изгибающего момента от действия временной нагрузки в рассматриваемых точках.

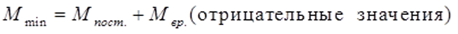
Полученные значения для удобства записи заносим в таблицу 1:

Таблица 1