Абсолютное, переносное и относительное

Движения точки

Сложное движение точки - это такое движение, при котором точка (тело) одновременно участвует в двух или нескольких движе­ниях. Например, сложное движение совершает лодка, переплываю­щая реку, пассажир, перемещающийся в вагоне движущегося поезда или по палубе плывущего парохода, а также человек, перемещающийся по лестнице движущегося эскалатора. Сложным является и движение шаров С и D центробежного регулятора Уатта (рис. 13.1), вращающегося вокруг вертикальной оси, когда при изменении нагрузки машины шары удаляются от этой оси или приближаются к ней, вращаясь со стерж­нями АС и BD вокруг шарниров А и В.

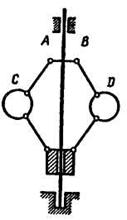
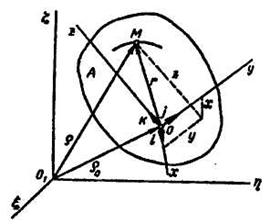
Рис. 13.1 Рис. 13.2

Рассмотрим движущееся тело А (рис. 13.2) и точкуМ, не принад­лежащую этому телу, а совершающую по отношению к нему некото­рое движение. Через произвольную точку О движущегося тела про­ведем неизменно связанные с этим телом оси x, у, z. Систему осей Охуz называют подвижной системой отсчета.

Неподвижной системой отсчета называют систему осей 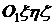, связанную с некоторым условно неподвижным телом, обычно с Землей.

Движение точки М относительно неподвижной системы отсчета называют абсолютным движением точки.

Скорость и ускорение точки в абсолютном движении называют абсолютной скоростью и абсолютным ускорением точки и обозна­чают 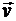и .

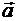Движение точки М относительно подвижной системы отсчета назы­вают относительным движением точки.

Скорость и ускорение точки в относительном движении называют относительной скоростью и относительным ускорением точки и обо­значают 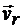и 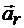(relatif-относительный).

Движение подвижной системы отсчета Охуz и неизменно связанного с ней тела А по отношению к неподвижной системе отсчета 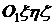является для точки М переносным движением. Точки тела А, совершая различные движения, имеют в данный момент различные скорости и ускорения. Скорость и ускорение точки тела А, связанного с под­вижной системой отсчета, совпадающей в данный момент с движу­щейся точкой, называют переносной скоростью и переносным ускоре­нием точки М и обозначают 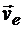и 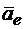(еmporter - увлекать).

Например, если человек идет вдоль радиуса вращающейся плат­формы (рис. 13.3), то с платформой можно связать подвижную систему отсчете, а с поверхностью Земли - неподвижную. Тогда движение платформы является переносным, движение человека по отношению к ней — относительным, а движение человека по отношению к Земле — абсолютным. Переносной скоростью человека 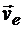, и его переносным ускорением 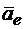являются скорость и ускорение той точки платформы, где находится в данный момент человек.

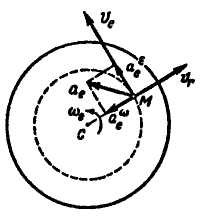
Рис. 13.3

Движение точки М (рис. 13.2) по отношению к неподвижной системе отсчета, которое названо абсолютным движением, является сложным, состоящим из относительного и переносного движений точки. Основная задача изучения сложного движения состоит в установле­нии зависимостей между скоростями и ускорениями относительного, переносного и абсолютного движений точки.

Положение точки М относительно неподвижной системы отсчета определяется радиусом-вектором 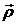, проведенным в точку М из начала этой системы O₁. Изменение радиуса-вектора 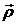характеризует абсо­лютное движение точки. Положение точки М относительно подвиж­ной системы отсчета определяется радиусом-вектором 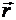, проведенным в точку М из начала этой системы О, или тремя координатами х, у, z в этой системе.

Изменение радиуса-вектора 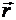или координат х, у, z точки М характеризует относительное движение точки. Таким образом, уравнения относительного движения точки имеют вид

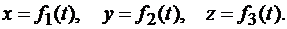
Изменение радиуса-вектора 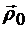, проведенного из начала неподвиж­ной системы координат О₁ в полюс О, характеризует абсолютное движение полюса.