Ускорение точек тела при его плоском движении

Ранее показано, что движение плоской фигуры в ее плоскости можно рассматривать как совокупность двух движений: поступатель­ного движения фигуры вместе с полюсом и ее вращения вокруг полюса.

Ускорения точек плоской фигуры определяются следующей теоре­мой: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки в ее вращении вместе с плоской фигурой вокруг полюса.

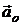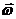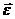Для установления этой зависимости допустим, что известны уско­рение некоторой точки О плоской фигуры и алгебраические вели­чины угловой скорости и углового ускорения плоской фигуры и , т. е. кроме модуле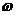й и 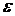известны направление вращения плоской фигуры в данный момент времени и характер ее вращения (ускоренное вращение или замедленное).

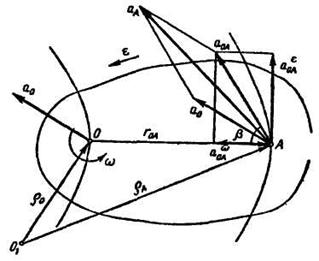
Рис. 11.9

Положим, что в данный момент времени фигура вращается уско­ренно в сторону, противоположную вращению часовой стрелки (рис. 11.9). Так как вращение фигуры ускоренное, то направим 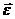в сторону 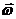. Определим ускорение любой точки А фигуры, приняв точку О за полюс.

Воспользуемся теоре­мой о скоростях точек плоской фигуры; на основании (5) имеем

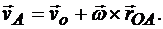
Ускорение точки А най­дем как векторную производную по времени от скорости этой точки:

.

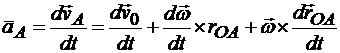Так как

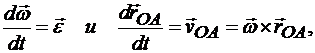
имеем

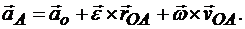
Здесь: 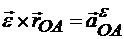- вращательное ускорение точки А во вращении вокруг полюса О; 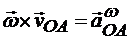- центростремительное ускорение точ­ки А во вращении вокруг полюса О.

Поэтому

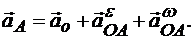(11.6)

Но геометрическая сумма вращательного и центростремительного ускорени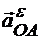й и 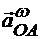является полным ускорением точки А в ее вра­щении вместе с плоской фигурой вокруг полюса О:

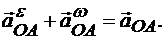
Окончательно получаем

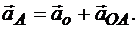
По формулам, приведенным ранее, находим модули:

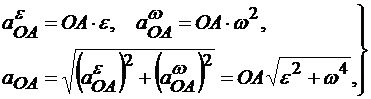
а также угол β:

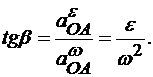
При ускоренном вращении вращательное ускорение 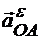направлено по отношению к полюсу в сторону вращения плоской фигуры, а при замедленном вращении - противоположно, т. е. направление 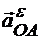по отношению к полюсу всегда соответствует направлению углового ускорения .

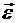Ускорение точки А плоской фигуры определяется путем построения многоугольника ускорений. На рис. 11.9 построен прямоугольник,определяющий ускорение точки А в ее вращательном движении вместе с плоской фигурой вокруг полюса О:

,

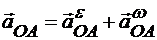а затем находятся ускорение точки 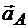как диагональ параллелограмма ускорений, сторонами которого служат ускорение полюса 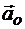и ускоре­ние точки во вращательном движении фигуры вокруг полюса .

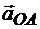Следствие 1. Проекция ускорения любой точки плоской фигуры на ось, проведенную uз произвольного полюса через эту точку, не может быть больше проекции ускорения полюса на ту же ось.

Если известно ускорение полюса О, ускорение точки А плоской фигуры определяется по формуле (11.6):

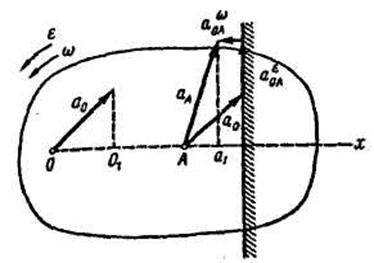
Рис. 11.10

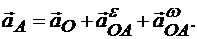
Сложим 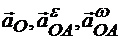правилу многоугольника, тогда 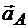будет замыкающей стороной многоугольника ускорений (рис. 11.10).

Проведем из полюса О через точку А ось х и спроецируем все эти векторы на эту ось:

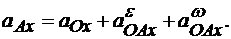
Проекция центростремительного ускорения 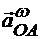на ось х всегда отрицательна, так как это ускорение направлено от точки А к полюсу О, т. е. Противоположно направлению оси х:

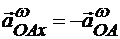
Проекция вращательного ускорения 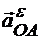на ось х равна нулю, так как это ускорение всегда перпендикулярно оси х:

.

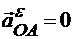На этом основании

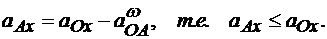
В этом заключается первое следствие теоремы об ускорениях точек плоской фигуры.

Проекции ускорений на ось, направленную из полюса, могут иметь знаки плюс и минус.

Из следствия вытекает, что алгебраическая величина проекции 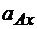меньше 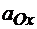, а абсолютное значение 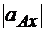может и пре­вышать 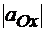при большом центростремительном ускорении 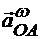. Про­екции ускорений точки А и полюса О на ось х равны в том случае, если 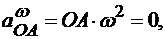т. е. при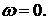

Проведем через конец ускорения полюса 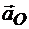, отложенного в точке А, прямую, перпендикулярную оси х. Эта прямая представляет собой годограф возможных ускорений точки плоской фигуры при 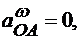т. е. при 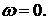, и является границей, за которую не могут выходить концы возможных ускорений точки А. Действительно, если 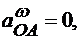то конец ускорения 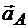обязательно находится на этой прямой, а если 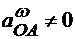, то конец ускорения 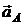находится с той стороны этой прямой, где расположен полюс.

Следствие 2. Концы ускорений точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между этими точками.

Зная ускорение 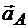точки А отрезка АВ, алгебраические величины угловой скорости 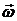и углового ускорения 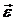, определим ускорение точки В отрезка, приняв точку А за полюс:

.

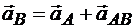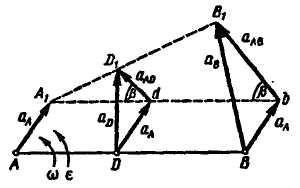
Рис. 11.11

Построим в точке В ускорение полюса 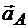(рис. 11.11). Положим, что отрезок вращается ускоренно в направлении, обратном направлению вращения часовой стрелки. Из конца ускорения 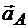отложим ускорение 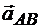под углом 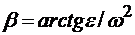к отрезку A₁b, равному и параллельному отрезку АВ. Соединив точку В с концом 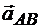, получаем ускорение точки В.

Для определения ускорения какой-либо другой точки отрезка, на­пример точки D, выполним аналогичное построение.

Очевидно, что ускорение 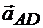составляет с отрезком А₁b тот же угол β.

Ускорения точек В и D отрезка в его вращательном движении вокруг полюса А пропорциональны расстояниям от этих точек до полюса. Действительно,

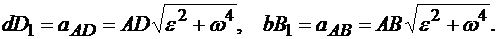
Поэтому dD₁/bB₁= AD/AB, но AD=A₁d и АВ=А₁b, как противопо­ложные стороны параллелограммов. Тогда

.

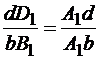Таким образом, 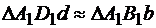. Из подобия треугольников следует, что:

Концы ускорений - точки a₁, d₁ и В₁ - лежат на oдной прямой;

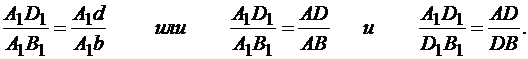
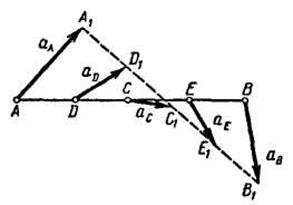
Рис. 11.12

Последнее соотношение показывает, что концы ускорений точек неизменяемого отрезка делят прямую, соединяющую эти концы, на части, пропорциональные расстояниям между соответствующими точ­ками.

Поэтому, зная ускорения 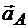и 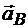концов отрезка АВ, можно определить графически ускорения любой точки этого отрезка.

Допустим, что требуется определить ускорение точек D, С и Е, делящих отрезок на четыре равные части (рис. 11.12). Соединяем концы ускорений точек А и В, отложенных в масштабе, отрезком прямой А₁В₁ и делим этот отрезок точками D₁, C₁ и E₁ на четыре равные части. Соединяя точки D и D₁, С и C₁, E и E₁, получаем ускорения этих точек 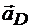, 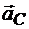и 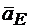. Пользуясь масштабом, находим их модули и по чертежу определяем их направления.

Лекция 12