Скорости точек тела при его плоском движении

Зависимость между скоростями точек плоской фигуры устанавливается по следующей теореме: скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и скорости этой точки в ее вращении вместе с плоской фигурой вокруг полиса.

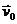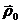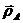Точку О, скорость которой равна , примем за полюс. Определим скорость любой другой точки плоской фигуры, например точки А (рис. 11.7). Для этого проведем из неподвижной точки плоскости О₁ в точки О и А радиусы-векторы и . Проведем также радиус-вектор 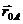полюса О в точку А.

Так как этот радиус-вектор соединяет две точки плоской фигуры, то за все время движения он вращается вокруг полюса с угловой скоростью плоской фигуры ω, не изменяясь по модулю.

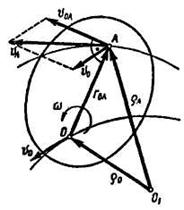
Рис. 11.7

За все время движения между радиусами-векторами сохраняется зависимость

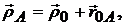
где модуль

.

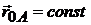Определим отсюда скорость точки А:

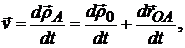
где 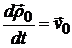- скорость полюса О.

Так как при движении плоской фигуры модуль радиуса-вектора 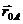остается неизменным, а направление его при повороте фигуры изме­няется, то производная 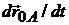представляет собой вращательную скорость точки А вокруг полюса О, которую обозначим :

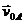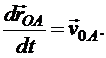
Вращательную скорость 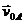можно представить в виде векторного произведения вектора угловой скорости плоской фигуры 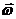на радиус-вектор :

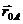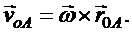
Вращательная скорость 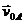направлена перпендикулярно отрезку ОА, в сторону вращения фигуры, и имеет модуль

.

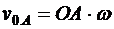После подстановки получаем

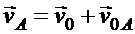(11.4)

или

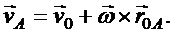(11.5)

Скорость точки А изображается диагональю параллелограмма, построенного при точке А на скорости полюса О, перенесенной в точку А, и вращательной скорости точки А вокруг полюса О (рис. 11.7).

Следствие I. Проекции скоростей точек плоской фигуры на ось, проходящую через эти точки, алгебраически равны.

Положим, что в данный момент времени известны скорость точки А плоской фигуры, направление ее вращения и модуль угловой скорости фигуры 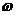(рис. 11.8). Приняв точку А за полюс, определим скорости точек В и D плоской фигуры, лежащих на одной прямой с точкой A:

. (11.6)

при этом вращательные скорости этих точек вокруг полюса A 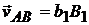и 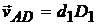направлены перпендикулярно отрезкам АВ и АD в сторону вращения фигуры.

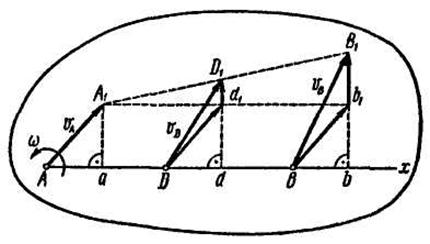
Рис 11.8

Проведем ось х через точки А, D и В и спроецируем скорости этих точек на ось х, тогда

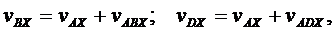
но 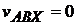и 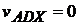так как векторы 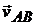и 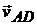перпендикулярны оси х. Поэтому

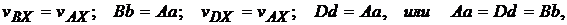
т. е. проекции скоростей всех точек отрезка АВ на ось х, направленную вдольэтого отрезка, равны между собой.

Следствие 2. Концы скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка.

Рассматривая рис. 11.8, устанавливаем, что

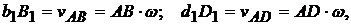
откуда

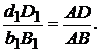
Так как 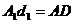и 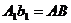как противоположные стороны параллелограммов, то

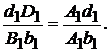
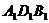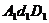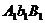Это соотношение показывает, что - отрезок прямой. Из подобия треугольников и имеем

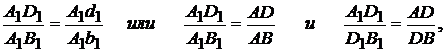
т.е. расстояния между концами скоростей пропорциональны расстояниям между соответствующими точками.