Равнопеременное движение точки

Равнопеременным движением по траектории любой формы называют движение, при котором касательное ускорение постоянно

.

Установим зависимости , соответствующие изменению скорости ( ) и дуговой координаты ( ) при равнопеременном движении. Известно, что

.

Разделим переменные и проинтегрируем это уравнение в пределах до и до

,

или

. (9.15)

Выражение (9.15) называется уравнением изменения скорости.

Если учесть, что , то подставив в уравнение изменения скорости, получим

или .

Вторично интегрируя это выражение в соответствующих пределах, получим

. (9.16)

Выражение (9.16) называется уравнением равнопеременного движения.

Графически изменения дуговой координаты ( ), скорости ( ) и касательного ускорения ( ) можно показать следующим образом (рис. 9.12).

Рис. 9.12

График равнопеременного движения (ускоренного) представлен ветвью параболы, график скорости – прямой, направленной под углом от оси абсцисс, график касательного ускорения – прямой, параллельной от оси абсцисс (рис. 12).

Рис. 9.13

В случае, когда равнопеременное движение замедленное, положение вогнутости параболы изменится на противоположное; прямая, представляющая график скорости изменит наклон к оси абсцисс (рис. 9.13).

Скорость изменится от некоторого значения до соответствующего остановке.

Пример. Автомобиль движется равномерно по закруглению радиусом м, причем ускорение его центра тяжести равно м/с². определить скорость центра тяжести автомобиля.

Решение. По условию задачи необходимо определить скорость центра тяжести автомобиля, поэтому задача сводится к кинематике точки. Движение точки задано естественным способом так как известна траектория движения, поэтому необходимо на рисунке показать эту траекторию – дугу радиусом , на ней выбрать начало и положительное направление отсчета дуговой координаты. Ограничений в задаче никаких не введено, мы вправе выбрать начало и направление отсчета дугой координаты самостоятельно. Будем считать, что движение автомобиля происходит только в одном направлении, т. е. в сторону увеличения дуговой координаты, поскольку об ином речь в задаче не идет.

Рис. 9.14

В случае равномерного криволинейного движения

,

где - радиус кривизны траектории в данной ее точке.

В нашем случае м в любой точке траектории. Окончательно имеем

м/с.

Покажем на рисунке в произвольном положении на траектории точку и изобразим ее скорость показав вектор скорости 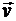, направленным в сторону возрастания дуговой координаты (рис. 9.14). Ускорение точки равно нормальному ускорению и направлено к центру кривизны траектории.

Таблица 9.1

Основные формулы по кинематике точки

Способы задания движения	Уравнение движения	Скорость м/с	Ускорение м/с2
Векторный
Координатный
Естественный
Равномерное движение
Равнопеременное движение

Лекция 10