Определение реакций опор составных
Конструкций
Статический расчет инженерных сооружений во многих случаях сводится к рассмотрению условий равновесия конструкций, состоящих из системы тел, соединенных шарнирами. Связи, соединяющие части конструкций между собой, называются внутренними, в отличие от внешних связей, скрепляющих конструкцию с телами, в нее входящими. Рассмотрим составную конструкцию типа арки (рис. 5.15, а). Конструкция является статически определимой системой.
При действии внешней нагрузки на конструкцию в каждой опоре возникает по две реакции, всего четыре неизвестные реакции. Вертикальные реакции обозначим через 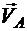 и
и 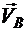 , горизонтальные - через
, горизонтальные - через 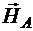 и
и 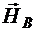 (рис. 5.15, б).
(рис. 5.15, б).
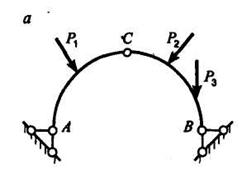
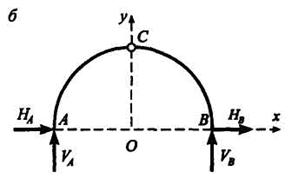
Рис. 5.15
Кроме трех уравнений равновесия для системы сил, расположенных в одной плоскости, для расчета конструкции можно составить четвертое уравнение, основанное на том, что линия действия равнодействующей всех сил, приложенных к левой (а также и к правой) половине, должна пройти через врезанный шарнир С, так как в противном случае равнодействующая создала бы не нулевой момент относительно шарнира С и левая (или правая) половина арки вращалась бы вокруг оси С.
Так как по теореме Вариньона момент равнодействующей равен алгебраической сумме моментов составляющих ее сил, то четвертое дополнительное уравнение можно сформулировать следующим образом.
Алгебраическая сумма моментов сил, действующих на левую или правую половину составной конструкции относительно точки С (внутреннего шарнира), равняется нулю, т.е.
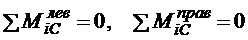 .
.
Задача 3. Однородные брусья АС и BD весом соответственно Р1 и Р2 расположены в вертикальной плоскости (рис. 3.1, а). Брусья свободно опираются друг на друга в точке С, а в точках А и В имеют неподвижные шарнирные опоры; в точке К брус BD закреплен невесомым стержнем.
Дано: Р1= 10 Н, Р2 = 20 Н, М1 = 20 Нм, F= 50 Н, l = 1 м, М2 = 30 Нм.
Определить реакции связей в точках А, В, С и К.
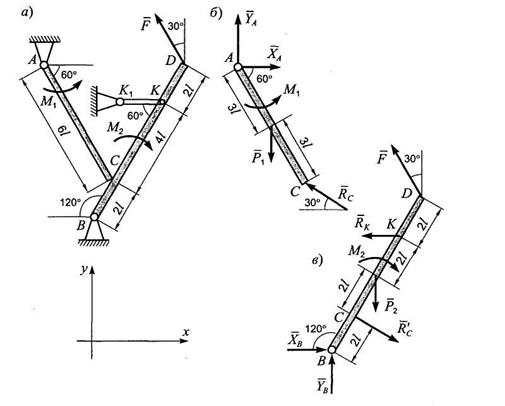
Рис. 3.1
Решение. Расчленим систему на две части и рассмотрим сначала равновесие бруса АС (рис. 3.1, б). Проведем координатные оси и изобразим действующие на брус АС силы: силу тяжести Р, пару сил с моментом М, реакции связей XA,YA, Re (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция Re направлена перпендикулярно брусу BD).
Для полученной плоской системы сил составим три уравнения равновесия:
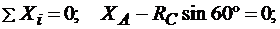 , (3.1)
, (3.1)
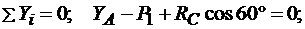 , (3.2)
, (3.2)
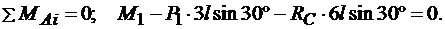 . (3.3)
. (3.3)
Теперь рассмотрим равновесие бруса BD (рис. 3.1, в). На него действуют сила тяжести Р2, сила F, реакции внешних связей ХВ, YB, RK и давление R’С со стороны бруса АС, которое на основании равенства действия и противодействия направлено противоположно силе RC.
Для полученной плоской системы сил тоже составим три уравнения равновесия:
 (3.4)
(3.4)
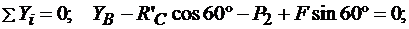 (3.5)
(3.5)
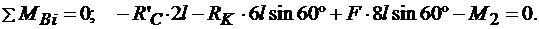 (3.6)
(3.6)
Решив систему уравнений (3.1) — (3.6) и учитывая при этом, что численно R'C = RC, найдем искомые реакции.
Ответ: ХA=1,44 Н, YA=9,17 Н, ХB = –26,06 Н, YB = –22,47 Н, RC = 1,66 H, RK = –52,5 Н.
Из полученных результатов видно, что силы ХВ, YB и RK направлены противоположно показанным на рис. 3.1, в.
Задача 4. На угольник ABC ( 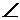 ABC = 90°), конец А которого жестко заделан, в точке С опирается стержень DE (рис. 3.2, а). Стержень имеет в точке D неподвижную шарнирную опору и к нему приложена пара с моментом М2, а к угольнику — равномерно распределенная на участке KB нагрузка интенсивности q и пара с моментом М1. Дано: M1 = 10 кНм, q = 4 кН/м, а = 1 м, М2 = 40 кНм. Определить реакции в точках А, С, D, вызванные заданными нагрузками.
ABC = 90°), конец А которого жестко заделан, в точке С опирается стержень DE (рис. 3.2, а). Стержень имеет в точке D неподвижную шарнирную опору и к нему приложена пара с моментом М2, а к угольнику — равномерно распределенная на участке KB нагрузка интенсивности q и пара с моментом М1. Дано: M1 = 10 кНм, q = 4 кН/м, а = 1 м, М2 = 40 кНм. Определить реакции в точках А, С, D, вызванные заданными нагрузками.
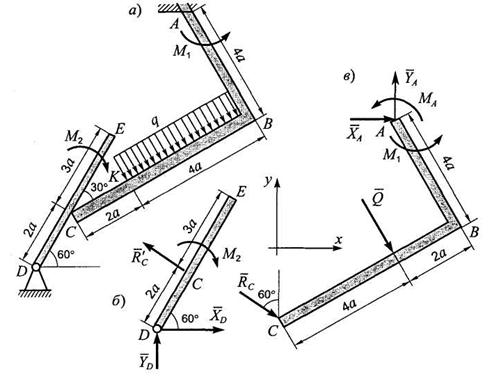
Рис. 3.2
Решение. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня DE (рис. 3.2, б). Проведем координатные оси и изобразим действующие на стержень силы и моменты: момент М2, реакцию R^, направленную перпендикулярно стержню, и составляющие XD и YD реакции шарнира D. Для полученной плоской системы сил составляем три уравнения равновесия:
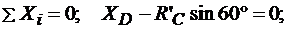 (3.7)
(3.7)
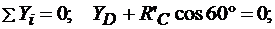 (3.8)
(3.8)
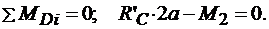 (3.9)
(3.9)
Теперь рассмотрим равновесие угольника (рис. 3.2, в). На него действуют сила давления стержня RС, направленная противоположно реакции R’C, равномерно распределенная нагрузка, которую заменяем силой Q, приложенной в середине участка KB (численно Q = q∙4a= 16 кН), пара сил с моментом M1 и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими ХА, YA, и пары с моментом МА. Для этой плоской системы сил тоже составляем три уравнения равновесия:
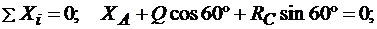 (3.10)
(3.10)
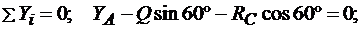 (3.11)
(3.11)
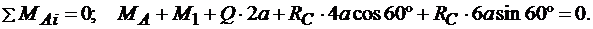 (3.12)
(3.12)
Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (3.7) — (3.12), найдем искомые реакции. При решении учитываем, что численно R’C = RC в силу равенства действия и противодействия.
Ответ: RC = 20 кН, YD = –10 кН, XD= 17,34 кН, ХА = –25,34 кН, YA = 23,87 кН, МА = –186,4 кНм.
Знаки указывают, что силы YD, XA и момент МА направлены противоположно показанным на рисунках.
Задача 5. Дана плоская составная конструкция с приложенными к ней нагрузками (рис. 3.3) Определить реакции шарниров А, В и С, если Р = 10 кН, q = 5 кН/м, М = 6 кНм, а = 1,2 м, b = 1 м, r = = 0,15 м. Нить невесомая, трением в подшипнике блока D пренебречь.
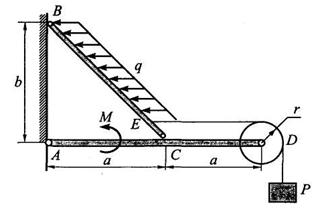
Рис. 3.3
Расчленим конструкцию на две части, освободив ее от шарниров А и В (внешние связи), шарнира С и горизонтальной нити (внутренние связи). Расчетные схемы изображены на рис. 3.4, а,б.
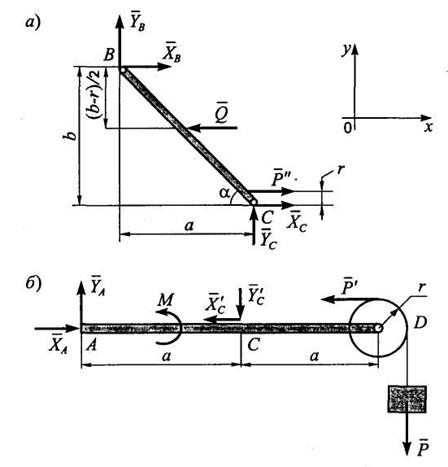
Рис. 3.4
На расчетных схемах обозначено:
XA,YA - составляющие реакции шарнира А;
ХВ, YB - составляющие реакции шарнира В;
ХС, YС - составляющие реакции шарнира С на балку ВС;
Х'C = –ХC, Y’C= –YC - составляющие реакции шарнира С на балку АС;
Р’ - реакция нити на блок D;
Р"- реакция нити на балку ВС;
Q - равнодействующая распределенной нагрузки.
Так как нить невесомая, а трением на блоке D пренебрегаем, то Р' = Р" = Р. Модуль равнодействующей распределенной нагрузки определяем по формуле
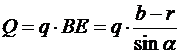 ,
,
где
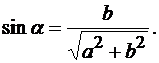
Составим уравнения равновесия балки ВС (рис. 3.4, а):
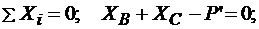 (3.13)
(3.13)
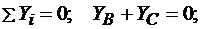 (3.14)
(3.14)
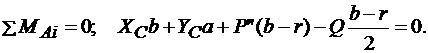 (3.15)
(3.15)
Система уравнений (1) — (3) содержит 4 неизвестных. Ее нужно дополнить системой уравнений равновесия для расчетной схемы, изображенной на рис. 3.4, б:
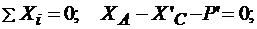 (3.16)
(3.16)
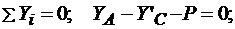 (3.17)
(3.17)
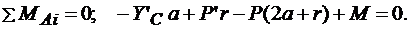 (3.18)
(3.18)
Решая систему уравнений (3.13)—(3.18), находим неизвестные.
Из уравнения (3.18) получаем
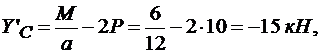
из уравнения (3.17)
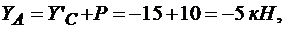
из уравнения (3.14)
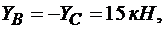
из уравнения (3.15)
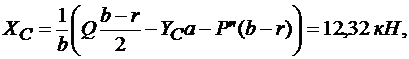
из уравнения (3.13)
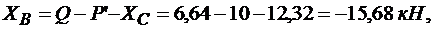
из уравнения (3.16)
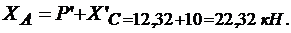
Ответ: ХА = 22,32 кН, ХВ =–1.5,68 кН, ХС = 12,32 кН; YA = –5 кН, YB = 15 кН, YС = –15 кН.
Замечание. Для определения искомых величин в данном примере можно было избрать другой путь решения: рассмотреть равновесие всей конструкции в целом как абсолютно твердого тела, освободив ее от связей в точках А и В (рис. 3.5) совместно с одной из частей (рис. 3.4, а или рис. 3.4, б).
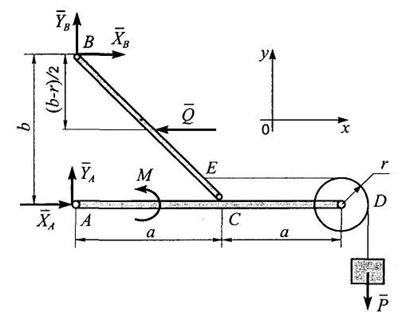
Рис. 3.5
Задача 6. Определить момент в заделке А и реакцию опоры В в составной конструкции, изображенной на рис. 3.6, если qmax = 5 кН/м, Р= 10 кН, М = 7 кНм, а = 4 м, b= 1,5 м, α = 60°.
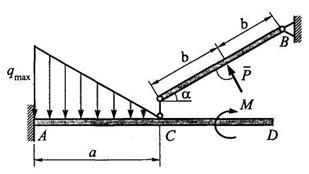
Рис. 3.6
Решение. Рассмотрим равновесие всей конструкции как абсолютно твердого тела, освободив ее от связей в точках А и В (рис. 3.7).
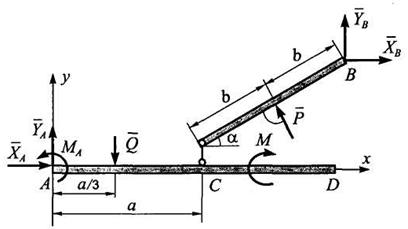
Рис. 3.7
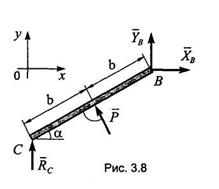 |
На рис. 3.7 обозначено:
XA,YA - составляющие реакции заделки;
МА - реактивный момент в заделке;
ХВ, YB - составляющие реакции шарнира В;
Q - равнодействующая распределенной нагрузки, модуль которой
Q = 0,5qmaх∙a = 0,5∙5∙4 = 10 кН;
Поскольку неизвестные ХА и YA определять не нужно, то из всех уравнений равновесия, которые можно составить для всей конструкции, следует взять только уравнение моментов относительно точки А, как не содержащее этих неизвестных:
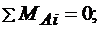
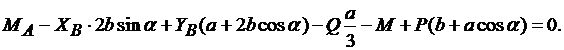 (3.19)
(3.19)
Рассмотрим далее равновесие балки ВС.
Расчетная схема изображена на рис. 3.8.
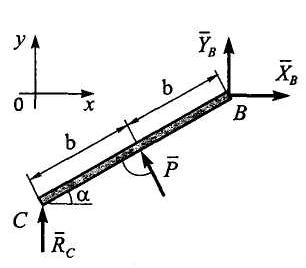
Рис. 3.8
Реакцию стержня RC определять не нужно. Поэтому для балки ВС составляем такие уравнения, в которые эта сила не входит:
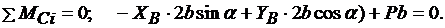 (3.20)
(3.20)
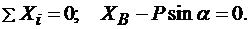 (3.21)
(3.21)
Система уравнений (3.19)—(3.21) содержит только те неизвестные, которые нужно определить.
Из уравнения (3.21) получаем
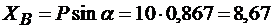 кН,
кН,
из уравнения (3.20)
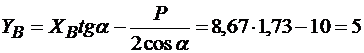 кН,
кН,
из уравнения (3.19)
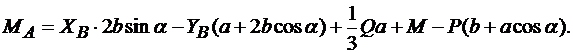 .
.
После вычислений
МА = – 19,67 кНм.
Ответ: МА = –19,67 кНм, ХB= –8,67 кН, YB = 5 кН.
Лекция 6
Трение
Трение покоя (сцепления)
Исследованием явления трения впервые занимался Леонардо да Винчи. В конце XVII в. французский физик Амонтон (1663-1705) установил независимость силы трения от величины поверхности соприкасания тел. Законы трения были сформулированы французским физиком Кулоном (1736-1806).
Если к твердому телу, покоящемуся на шероховатой горизонтальной плоскости (рис. 6.1), приложить горизонтальную силу  , то действие этой
, то действие этой
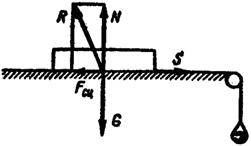
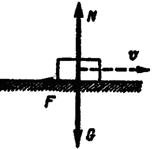
Рис. 6.1 Рис. 6.2
силы вызовет появление силы сцепления 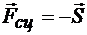 , представляющей собой силу противодействия плоскости смещению тела. Благодаря сцеплению тело остается в покое при изменении модуля силы
, представляющей собой силу противодействия плоскости смещению тела. Благодаря сцеплению тело остается в покое при изменении модуля силы  от нуля до некоторого значения
от нуля до некоторого значения 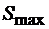 . Это значит, что модуль силы сцепления тоже изменяется от
. Это значит, что модуль силы сцепления тоже изменяется от 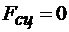 до
до 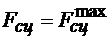 в момент начала движения.
в момент начала движения.
Модуль максимальной силы сцепления, как показывает опыт, пропорционален нормальному давлению N тела на плоскость. В рассматриваемом случае N = G. Тогда
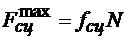 .
.
Коэффициент пропорциональности 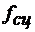 является отвлеченным числом и называется коэффициентом сцепления.
является отвлеченным числом и называется коэффициентом сцепления.
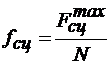
Коэффициент сцепления зависит от материала и физического состояния соприкасающихся тел и определяется экспериментально. Его величина для материалов, используемых в технике, обычно меньше единицы. Так как максимальное значение силы сцепления равно 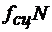 , то модуль силы сцепления всегда удовлетворяет условию
, то модуль силы сцепления всегда удовлетворяет условию
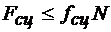 .
.
Направление силы сцепления противоположно направлению того движения, которое возникло бы под действием приложенных к телу сил при отсутствии сцепления.
При скольжении тела по шероховатой поверхности к нему прилажена сила трения скольжения. Направление этой силы, противодействующей скольжению, противоположно направлению скорости тела (рис. 6.2).
Модуль силы трения скольжения пропорционален нормальному давлению N:
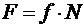 .
.
Коэффициент пропорциональности f называется коэффициентом трения скольжения и определяется опытным путем.
Коэффициент трения скольжения является отвлеченной величиной и зависит от материала и физического состояния трущихся поверхностей, а также от скорости движения тела и удельного давления.
Однако в элементарных расчетах зависимость коэффициента трения скольжения от скорости и удельного давления часто не учитывается.
