Сложение пар сил и Условия равновесия пар сил
Рассмотрим сложение двух пар сил, расположенных в пересекающихся плоскостях, и докажем следующую теорему: геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары.
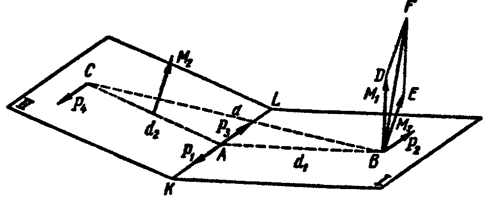
Рис. 3.13
Пусть требуется сложить две пары сил, расположенные в пересекающихся плоскостях 1 и 2 и имеющие моменты 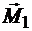 и
и 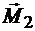 (рис. 3.13). Выбрав силы этих пар равными по модулю
(рис. 3.13). Выбрав силы этих пар равными по модулю
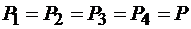 ,
,
определим плечи этих пар:
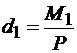 и
и 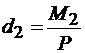 .
.
Расположим эти пары сил таким образом, чтобы силы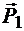 и
и 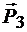 былинаправлены по линии пересечения плоскостей KL в противоположные стороны и уравновешивались. Оставшиеся силы
былинаправлены по линии пересечения плоскостей KL в противоположные стороны и уравновешивались. Оставшиеся силы 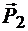 и
и 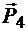 образуютпару сил, эквивалентную данным двум парам сил. Эта пара силимеетплечоВC=d и момент, перпендикулярный плоскости действия парысил,равный по модулю М = Pd.
образуютпару сил, эквивалентную данным двум парам сил. Эта пара силимеетплечоВC=d и момент, перпендикулярный плоскости действия парысил,равный по модулю М = Pd.
Покажем, что геометрическая сумма моментов составляющих пар сил, равна моменту эквивалентной пары. Так как момент пары сил является свободным вектором, перенесем моменты составляющих пар сил 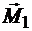 и
и 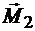 в точку В и сложим их, построив на этих моментах параллелограмм.
в точку В и сложим их, построив на этих моментах параллелограмм.
Докажем, что диагональ 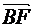 =
= 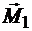 +
+ 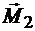 представляет собой момент эквивалентной пары
представляет собой момент эквивалентной пары 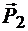 ,
, 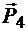 . Для этого необходимо доказать, что:
. Для этого необходимо доказать, что:
1) BF =Pd;
2) отрезок BF перпендикулярен плоскости действия эквивалентной пары сил;
3) смотря навстречу вектору 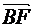 , можно видеть пару
, можно видеть пару 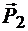 ,
, 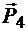 стремящейся вращать плоскость в сторону, обратную вращению часовой стрелки.
стремящейся вращать плоскость в сторону, обратную вращению часовой стрелки.
Д о к а з а т е л ь с т в о.
1. Треугольники ВАС и BDF подобны, так как
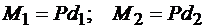 ;
;
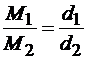 т. е.
т. е. 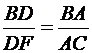 .
.
и 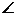 BDF=
BDF= 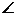 ВАС как углы с взаимно перпендикулярными сторонами. Из подобия этих треугольников следует, что
ВАС как углы с взаимно перпендикулярными сторонами. Из подобия этих треугольников следует, что
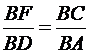 т. е.
т. е. 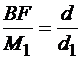 ,
,
откуда
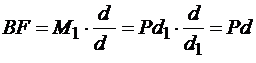 .
.
Так как вектор момента каждой пары сил перпендикулярен плоскости действия этой пары сил, то
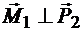 и
и 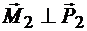 ,
,
а поэтому плоскость параллелограмма BDFE перпендикулярнасилепары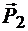 и
и 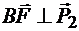 .
.
Кроме того, 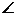 DBA =90° и
DBA =90° и 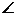 СВА =
СВА = 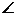 FBD, откуда
FBD, откуда 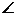 CBF =90°, т.е. BF
CBF =90°, т.е. BF 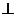 ВС.
ВС.
Так как диагональ параллелограмма BF перпендикулярна силе пары 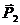 и плечу пары сил ВС, то она перпендикулярна плоскости действия эквивалентной пары сил.
и плечу пары сил ВС, то она перпендикулярна плоскости действия эквивалентной пары сил.
3. Выполнение третьего условия показано на рисунке 3.13. Смотря навстречу вектору BF, можно видеть пару 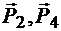 стремящейся вращать плоскость ее действия в сторону, обратную вращению часовой стрелки.
стремящейся вращать плоскость ее действия в сторону, обратную вращению часовой стрелки.
Из выше изложенного следует, что вектор 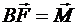 , т. е. геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары сил:
, т. е. геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары сил:
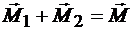 .
.
Установленное правило сложения моментов пар сил называется правилом параллелограмма моментов. Построение параллелограмма моментов можно заменить построением треугольника моментов.
Применяя построение параллелограмма или треугольника моментов, можно решить и обратную задачу, т. е. разложить любую пару сил на две составляющие.
Пусть требуется сложить несколько пар сил, расположенных произвольно в пространстве (рис. 3.14). Определив моменты этих пар, их можно перенести в любую точку О пространства. Складывая последовательно моменты этих пар сия, можно построить многоугольник моментов пар, замыкающая сторона которого определит момент эквивалентной им пары сил.
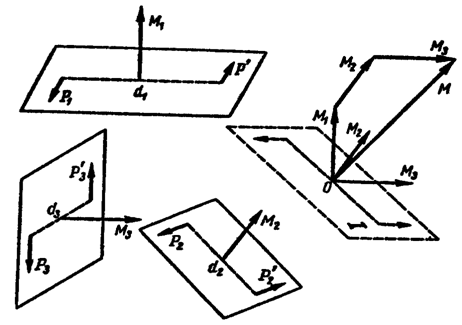
Рис. 3.14
На рисунке 3.14 показано построение многоугольника моментов при сложении трех пар сил.
Момент пары сил, эквивалентной данной системе пар сил в пространстве, равен геометрической сумме моментов составляющих пар сил:
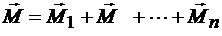 ,
,
или
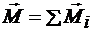 . (3.8)
. (3.8)
Плоскость 1 действия этой пары сил перпендикулярна направлению ее момента 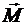 . Если момент эквивалентной пары сил равен нулю, то пары сил взаимно уравновешиваются:
. Если момент эквивалентной пары сил равен нулю, то пары сил взаимно уравновешиваются:
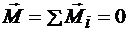 . (3.9)
. (3.9)
Таким образом, условие равновесия пар сил, произвольно расположенных в пространстве, можно сформулировать так: пары сил, произвольно расположенные в пространстве, взаимно уравновешиваются в том случае, если геометрическая сумма их моментов равна нулю.
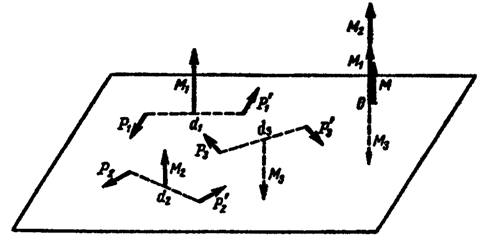
Рис. 3.15
Если пары сил расположены в одной плоскости (рис. 3.15), то моменты этих пар сил, направленные по одной прямой, складываются алгебраически.
Момент пары сил, эквивалентной системе пар сил на плоскости. равен алгебраической сумме моментов составляющих пар:
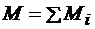 ,
,
где
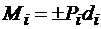 .
.
Условие равновесия
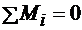 ,
,
т. е. пары сил, расположенные в одной плоскости, взаимно уравновешиваются, если алгебраическая сумма их моментов равна нулю.
Условия равновесия пар
Для равновесия пар сил, действующих на твердое тело, необходимо и достаточно, чтобы момент эквивалентной (результирующей) пары был бы равен нулю:
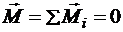 . (3.10)
. (3.10)
Проецируя формулу (3.10) на декартовы координатные оси, получаем три скалярных выражения:
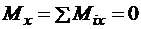 ,
,
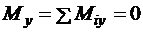 , (3.11)
, (3.11)
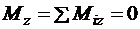 .
.
Из выражения (3.11) следует, чтобы уравновесить систему, состоящую из пар сил, необходимо приложить уравновешивающую пару, т. е. пару сил можно уравновесить другой парой сил с равными модулями и противоположно направленными моментами.
Пару сил невозможно уравновесить одной силой или какой-либо системой сил, отличной от пары сил.
Задача 1. Найти результирующую пару, которая уравновесила бы две пары сил с моментами 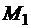 = 14 Нм,
= 14 Нм, 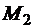 = 40 Нм, приложенные к балке АВ длиной 2 м (рис. 3.16).
= 40 Нм, приложенные к балке АВ длиной 2 м (рис. 3.16).
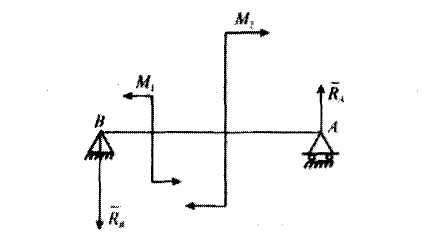
Рис. 3.16
Решение. Используя принцип освобождаемости от связей, заменяем действие опор на балку реакциями 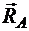 и
и 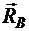 . Вектор силы
. Вектор силы 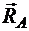 перпендикулярен опорной поверхности. Вектор силы
перпендикулярен опорной поверхности. Вектор силы 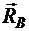 должен быть параллелен
должен быть параллелен 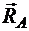 , так как они должны образовать эквивалентную результирующую пару.
, так как они должны образовать эквивалентную результирующую пару.
Исходя из условия равновесия пар сил, запишем:
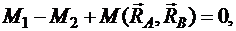
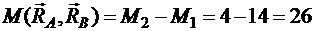 Нм.
Нм.
Так как дана длина балки, то можно найти силы, образующие результирующую пару:
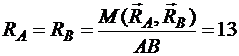 Нм.
Нм.
Задача 2. Балка длиной АВ= 10 м имеет шарнирно-неподвижную опору А и шарнирно-подвижную опору В с наклонной опорной плоскостью, составляющей с горизонтом угол α=30о (рис. 3.17). На балку действуют три пары сил, лежащие в одной плоскости, абсолютные значения моментов которых равны |M1|=8 кH∙м; |M2|=10 кН∙м; |М3|=7кН∙м.
Определить реакции опор.
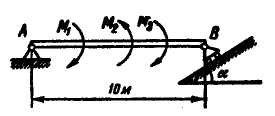
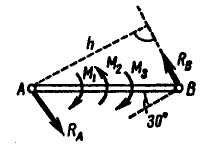
Рис 3.17 Рис. 3.18
Решение. Рассмотрим равновесие сил, приложенных к балке АВ: трех пар сил, реакции опоры 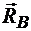 , направленной перпендикулярно опорной плоскости, и реакции опоры
, направленной перпендикулярно опорной плоскости, и реакции опоры 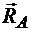 , линия действия которой не известна. Так как нагрузка состоит только из пар сил, лежащих в одной плоскости, то реакции опор
, линия действия которой не известна. Так как нагрузка состоит только из пар сил, лежащих в одной плоскости, то реакции опор 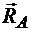 и
и 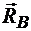 , должны составить пару сил, лежащую в той же плоскости. Направим реакцию
, должны составить пару сил, лежащую в той же плоскости. Направим реакцию 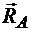 параллельно реакции
параллельно реакции 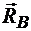 , чтобы силы
, чтобы силы 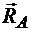 и
и 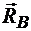 составили пару сил, направленную в сторону, обратную вращению часовой стрелки (рис. 3.18).
составили пару сил, направленную в сторону, обратную вращению часовой стрелки (рис. 3.18).
Для четырех пар сил, приложенных к балке, используем условие равновесия пар сил, лежащих в одной плоскости:
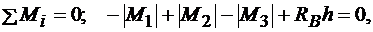
где 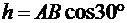 .
.
Отсюда
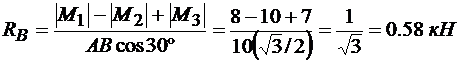 .
.
Знак плюс в ответе указывает, что принятое направление реакций опор 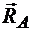 и
и 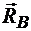 совпадает с истинным:
совпадает с истинным:
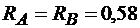 кН.
кН.
Лекция 4
