Событие. Классификация событий
Событие. Классификация событий
Событием называется любой факт, который в результате опыта может произойти или не произойти. События обозначают заглавными буквами латинского алфавита.
Достоверным называется событие, которое непременно произойдет при определенной совокупности условий.
Невозможным называется событие, которое заведомо не произойдет при определенной совокупности условий.
Случайным, называется событие, которое при определенных условиях может произойти или не произойти.
Два события называются совместными в данном опыте, если появление одного не исключает появление другого.
Два события называются несовместным, если они не могут произойти в одном испытании.
Несколько событий называются несовместными, если они попарно несовместны.
Два события называются противоположными, если появление одного равносильно непоявлению другого.
Множество событий 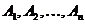 называются полной группой событий, если они попарно несовместны; появление одно и только одного из них является достоверным событием. Например, шесть граней кубика образуют полную группу событий.
называются полной группой событий, если они попарно несовместны; появление одно и только одного из них является достоверным событием. Например, шесть граней кубика образуют полную группу событий.
События называются равновозможными, если нет оснований полагать, что одно событие более возможно, чем другие.
Каждое событие, которое может наступить в процессе опыта, называется элементарным исходом.
Вероятность события. Свойства вероятности. Классическая вероятность
Для качественного сравнения событий вводится определенная мера, которая называется вероятностью события.
Классическое определение вероятности 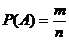 ,
, 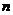 - общее число исходов,
- общее число исходов, 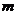 - число благоприятствующих исходов.
- число благоприятствующих исходов.
Свойства вероятности:
1. Вероятность достоверного события равна единице. Обозначим 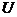 - достоверное событие, т.е.
- достоверное событие, т.е. 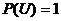 ,
, 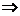
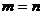 .
.
2. Вероятность невозможного события равна нулю. Обозначим 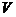 - невозможное событие, т.е.
- невозможное событие, т.е. 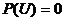 ,
, 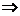
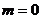 .
.
3. Вероятность случайного события выражается положительным числом, меньшим 1. Поскольку для случайного события  выполняются следующие неравенства
выполняются следующие неравенства 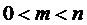 или
или 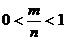 ,
, 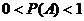 .
.
4. Вероятность любого события 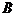 удовлетворяет неравенству
удовлетворяет неравенству 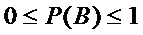 .
.
Геометрическая вероятность
Классическое определение вероятности предполагает, что число элементарных исходов конечно. На практике встречаются опыты, для которых множество таких исходов бесконечно. Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятность – вероятность попадания точки в область.
Обозначим меру области g (длину, площадь, объем) через mes g, а меру G – через mes G (mes первые три буквы французского слова 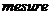 , что значит мера); обозначим буквой
, что значит мера); обозначим буквой  событие “попадания брошенной точки в область g, содержащейся в области G.” Вероятность попадания в область g точки, брошенной в область G, определяется формулой:
событие “попадания брошенной точки в область g, содержащейся в области G.” Вероятность попадания в область g точки, брошенной в область G, определяется формулой:
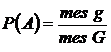 .
.
Пример. Найти вероятность того, что расстояние от брошенной точки, брошенной на отрезок единичной длины, до концов отрезка 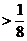 .
.
Решение. 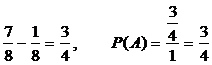 .
.
Задача о встрече
Два студента договорились о встрече в некоторый промежуток времени [0,T], причем каждый из них приходит к месту встречи случайным образом и ждет другого не более τ минут. Найти вероятность встречи студентов.
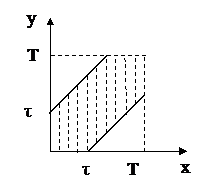 Пусть х и у – моменты прихода студентов к месту встречи. Областью равновозможных значений х и у является квадрат площадью
Пусть х и у – моменты прихода студентов к месту встречи. Областью равновозможных значений х и у является квадрат площадью 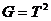 . Встреча произойдет, если
. Встреча произойдет, если 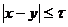 . Этому неравенству удовлетворяют точки, лежащие в заштрихованной полосе. Площадь полосы
. Этому неравенству удовлетворяют точки, лежащие в заштрихованной полосе. Площадь полосы 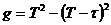 . Тогда
. Тогда
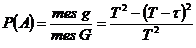 .
.
Действия над событиями
Суммой, или объединением, двух событий называется событие, состоящее в появлении хотя бы одного из них. Сумма событий  и
и 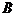 обозначается как
обозначается как 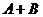 или
или 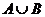 .
.
Аналогично определяется и обозначается сумма 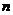 событий – то есть событие, состоящее в появлении хотя бы одного из них. Сумму
событий – то есть событие, состоящее в появлении хотя бы одного из них. Сумму 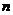 событий
событий 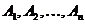 обозначают так:
обозначают так:
А1+А2+…+Аn= 
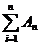 или А1È А2È…ÈАn=
или А1È А2È…ÈАn= 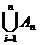
 |

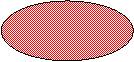
B 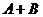 – попадание точки в окрашенную область (например, выпа-
– попадание точки в окрашенную область (например, выпа-
дение четного числа очков при бросании игральной кости (2)+(4)+(6)).
Произведением или пересечением двух событий называется событие, состоящее в одновременном их появлении. Произведение событий  и
и 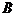 обозначается через
обозначается через 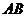 или
или 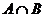 . Аналогично определяется произведение n событий. Произведение n событий
. Аналогично определяется произведение n событий. Произведение n событий 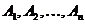 обозначают: А1А2…Аn=
обозначают: А1А2…Аn= 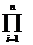 Аi или А1ÇА2Ç…ÇАn=
Аi или А1ÇА2Ç…ÇАn=  Ai
Ai
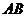 - попадание точки в заштрихованную область.
- попадание точки в заштрихованную область.

 |
Операции объединения и пересечения событий обладают некоторыми свойствами, аналогичными операциям умножения и сложения.
Эти операции коммутативны: AÈB=BÈA, AÇB=BÇA
ассоциативны: (AÈB)ÈC=AÈ(BÈC)=(AÈC)ÈB
(AÇB)ÇC=AÇ(BÇC)=(AÇC)ÇB
дистрибутивны: (AÈB)ÇС=(АÇС)È(BÇС).
Разностью событий  и
и 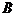 называется событие
называется событие 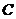 , которое означает, что наступает событие
, которое означает, что наступает событие  и не происходит событие
и не происходит событие 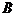 . Разность
. Разность  и
и 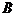 обозначается так:
обозначается так: 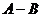 или
или 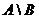 .
.
Формула полной вероятности
Следствием обеих теорем - теоремы сложения и умножения - является так называемая формула полной вероятности.
Пусть требуется определить вероятность некоторого события  , которое может произойти вместе с одним из событий
, которое может произойти вместе с одним из событий 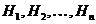 , образующих полную группу несовместных событий. Будем называть эти события гипотезами.
, образующих полную группу несовместных событий. Будем называть эти события гипотезами.
Докажем, что в этом случае
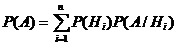 , (*)
, (*)
т. е. вероятность события  вычисляется как сумма произведений вероятности любой гипотезы на вероятность события при этой гипотезе.
вычисляется как сумма произведений вероятности любой гипотезы на вероятность события при этой гипотезе.
Формула (*) носит название формулы полной вероятности.
Доказательство. Так как гипотезы 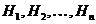 образуют полную группу событий, то событие
образуют полную группу событий, то событие  может появиться только в комбинации с какой-либо из этих гипотез
может появиться только в комбинации с какой-либо из этих гипотез
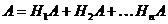 .
.
Т. к. гипотезы 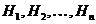 несовместны, то и комбинации
несовместны, то и комбинации 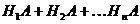 - также несовместны. Покажем это -
- также несовместны. Покажем это - 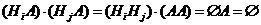 . Применяя к ним теорему сложения, получим
. Применяя к ним теорему сложения, получим
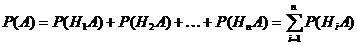 .
.
Применяя к событию 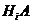 теорему умножения, получим
теорему умножения, получим
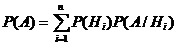 ,
,
что и требовалось доказать.
Пример. На фабрике, изготовляющей болты, первая машина производит 30% , вторая- 25% , третья- 45% всех изделий. Брак в их продукции составляет соответственно 2% , 1% и 3% . Найти вероятность того, что случайно выбранный болт оказался дефектным.
Решение. Обозначим через  событие, состоящее в том, что случайно выбранный болт – дефектный, а через
событие, состоящее в том, что случайно выбранный болт – дефектный, а через 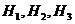 – события, состоящие в том, что этот болт произведен соответственно 1-ой, 2-ой и 3-ей машинами. Из условия задачи следует, что
– события, состоящие в том, что этот болт произведен соответственно 1-ой, 2-ой и 3-ей машинами. Из условия задачи следует, что 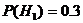 ,
, 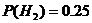 ,
, 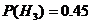 ;
; 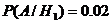 ,
, 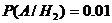 ,
, 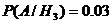 .
.
По формуле полной вероятности получаем, что 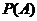 =0.3·0.02+0.25·0.01+0.45·0.3=0.022.
=0.3·0.02+0.25·0.01+0.45·0.3=0.022.
Закон распределения
Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана, с вероятностной точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вероятностью обладает каждое из событий 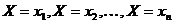 . Этим мы установим так называемый закон распределения случайной величины.
. Этим мы установим так называемый закон распределения случайной величины.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину будем говорить, что она подчинена данному закону распределения.
Формой задания закона является таблица
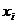 | 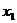 | 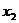 | 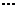 | 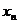 |
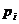 | 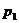 | 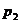 |  | 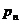 |
Такую таблицу мы будем называть рядом распределения случайной величины X.
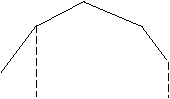
Графическое изображение ряда распределения называется многоугольником распределения 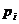 .
.
 |
| |||
 p1
p1
 xi
xi
x1 x2 x3 … xn
Многоугольник распределения - также одна из форм закона распределения.
Функция распределения
Мы рассмотрели закон распределения дискретной случайной величины. Для непрерывной случайной величины такую характеристику построить нельзя. Непрерывная случайная величина имеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток (несчетное множество). Для непрерывной случайной величины не существует ряда распределения, как он существует для дискретной величины. Но различные области возможных значений случайных величин все же не является одинаково вероятными, и для непрерывной величины существует распределение вероятностей, хотя и не в том смысле, как для прерывной.
Для количественной характеристики, этого распределения вероятностей удобно воспользоваться не вероятностью события 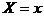 , а вероятностью события
, а вероятностью события 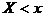 , где
, где  – некоторая текущая переменная. Вероятность этого события есть некоторая функция от
– некоторая текущая переменная. Вероятность этого события есть некоторая функция от  . Эта функция называется функцией распределения случайной величины
. Эта функция называется функцией распределения случайной величины  и обозначается
и обозначается 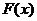 ,
, 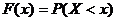 .
.
Функцию распределения 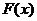 иногда называют также интегральной функцией распределения или интегральным законом распределения. Функция распределения есть самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как дискретных, так и непрерывных. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т. е. является одной из форм закона распределения.
иногда называют также интегральной функцией распределения или интегральным законом распределения. Функция распределения есть самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как дискретных, так и непрерывных. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т. е. является одной из форм закона распределения.
Плотность распределения
Пусть имеется непрерывная случайная величина  с функцией распределения
с функцией распределения 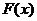 , которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от
, которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от  до
до 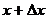 .
.
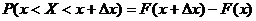 ,
,
т.е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать Dx®0. В пределе получим производную от функции распределения
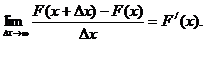
Обозначим 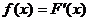 . (*)
. (*)
Функция 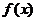 - производная функции распределения, характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (плотностью вероятности) непрерывной случайной величины
- производная функции распределения, характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (плотностью вероятности) непрерывной случайной величины  . Иногда
. Иногда 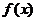 называют дифференциальной функцией распределения или дифференциальным законом распределения величины
называют дифференциальной функцией распределения или дифференциальным законом распределения величины  .
.
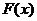
 |


Плотность распределения так же, как и функция распределения есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.
Рассмотрим непрерывную случайную величину  с плотностью распределения
с плотностью распределения 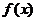 и элементарный участок
и элементарный участок 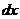 , примыкающий к точке
, примыкающий к точке  . Вероятность попадания случайной величины
. Вероятность попадания случайной величины  на этот элементарный участок есть
на этот элементарный участок есть 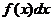 .
.
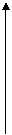
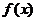
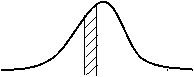

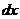

Выразим вероятность попадания величины  на отрезок от
на отрезок от 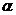 до
до 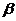 через плотность распределения. Очевидно, оно равно
через плотность распределения. Очевидно, оно равно
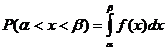 .
.
Формула (*) выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. По определению
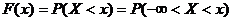 ,
,
откуда 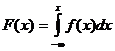 .
.
Мода и медиана
Кроме важнейшей из характеристик наложения - математического ожидания - на практике иногда применяются и другие характеристики наложения, в частности, мода и медиана случайной величины.
Модой случайной величины называется ее наиболее вероятное значение. Термин “наиболее вероятное значение”, строго говоря, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна. Обозначается буквой 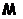 .
.
 Pi f(x)
Pi f(x)








 | |||
 |




 0
0  xi 0
xi 0  x
x
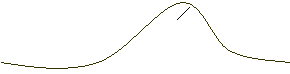
Часто применяется еще одна характеристика положения – медиана случайной величины. Медианой случайной величины  называется такое ее значение
называется такое ее значение 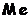 , для которого
, для которого
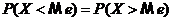
т.е. одинаково вероятно, окажется ли случайная величина меньше или больше 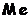 . Геометрически медиана, это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.
. Геометрически медиана, это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.
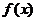
 | |||
 |
















 | |||
 | |||
Формула Бернулли
Пусть некоторый опыт воспроизводится 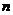 раз и каждый раз событие
раз и каждый раз событие  может наступать с одной и той же вероятностью
может наступать с одной и той же вероятностью 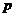 , независимо от результатов предыдущих опытов. В этом случае говорят о повторных независимых испытаниях. При этом событие
, независимо от результатов предыдущих опытов. В этом случае говорят о повторных независимых испытаниях. При этом событие  может наступать 0, 1, 2, … ,
может наступать 0, 1, 2, … , 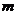 , … ,
, … , 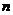 раз. Число наступлений события – это случайная величина. Найдем вероятность, с которой событие
раз. Число наступлений события – это случайная величина. Найдем вероятность, с которой событие  наступит
наступит 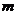 раз. Эту вероятность обычно обозначают символом
раз. Эту вероятность обычно обозначают символом 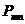 . Интересующее нас событие – наступление
. Интересующее нас событие – наступление 
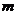 раз в
раз в 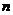 испытаниях, можно разбить на частные случаи, каждый из которых определяется номерами тех испытаний, в которых наступает
испытаниях, можно разбить на частные случаи, каждый из которых определяется номерами тех испытаний, в которых наступает  . Пусть
. Пусть 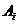 - это наступление
- это наступление  в
в 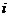 -ом испытании. Набор таких
-ом испытании. Набор таких 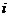 определяет отдельный случай. Например, (
определяет отдельный случай. Например, ( 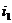 ,
, 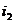 ,…,
,…, 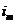 )- это случай, когда
)- это случай, когда  наступило в
наступило в 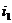 -ом испытании, затем
-ом испытании, затем 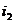 -ом и т.д., во всех же остальных испытаниях
-ом и т.д., во всех же остальных испытаниях  не наступило. Всех случаев будет столько, сколькими способами мы можем выбрать m натуральных чисел из
не наступило. Всех случаев будет столько, сколькими способами мы можем выбрать m натуральных чисел из 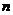 (1,2,3,…,
(1,2,3,…, 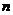 ), т. е. число всех случаев – это число сочетаний из
), т. е. число всех случаев – это число сочетаний из 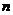 элементов по
элементов по 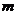 :
:
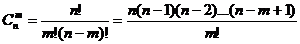
Найдем вероятность отдельного случая. Чтобы он наступил, должны наступить события 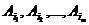 и события
и события 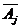 , где
, где 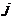 пробегает те числа из 1,2,3,…,
пробегает те числа из 1,2,3,…, 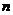 , которые отличны от
, которые отличны от 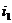 ,
, 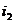 ,…,
,…, 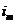 . Так как все указанные события независимы и операция умножения событий коммутативна, то вероятность отдельного случая
. Так как все указанные события независимы и операция умножения событий коммутативна, то вероятность отдельного случая
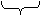
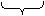
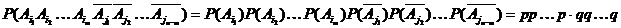
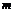
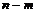
где 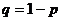 .
.
Мы видим, что все частные случаи равновозможны, поэтому, применяя теорему сложения для несовместных событий, получаем
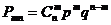 - формула Бернулли.
- формула Бернулли.
Пример. Пусть всхожесть семян ржи составляет 90%. Чему равна вероятность того, что из 7 посеянных семян взойдет 5?
Решение. Вероятность всхожести отдельного семени 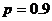 , следовательно,
, следовательно, 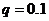 . По формуле Бернулли находим вероятность
. По формуле Бернулли находим вероятность
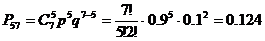 .
.
Неравенство Маркова
Теорема. Если случайная величина 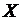 может принимать только неотрицательные значения и у нее есть математическое ожидание, то какова бы ни была величина
может принимать только неотрицательные значения и у нее есть математическое ожидание, то какова бы ни была величина 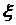 той же размерности, что и
той же размерности, что и 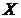 , всегда выполняется неравенство
, всегда выполняется неравенство
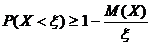 .
.
Доказательство. Пусть 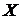 - непрерывная случайная величина с плотностью распределения
- непрерывная случайная величина с плотностью распределения 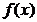 . Из условия теоремы следует, что
. Из условия теоремы следует, что 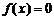 при
при 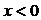 и
и 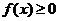 при
при 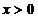 .
.
Математическое ожидание случайной величины 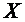 -
-
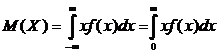 (разобьем на два интеграла)
(разобьем на два интеграла)
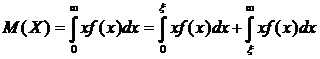 .
.
Так как 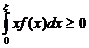 , то
, то 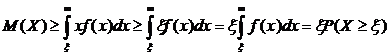 .
.
Итак,
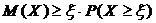 ,
, 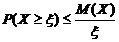 .
.
Если это неравенство вычесть из тождества 1=1, то
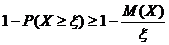 или
или 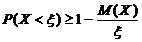 . Что и требовалось доказать.
. Что и требовалось доказать.
Пример. Средний срок службы мотора 4 года. Оценить снизу вероятность того, что данный мотор не прослужит 20 лет.
Решение. Пусть случайная величина 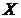 - срок службы мотора. Из условия задачи -
- срок службы мотора. Из условия задачи - 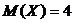 . Требуется оценить снизу вероятность
. Требуется оценить снизу вероятность 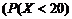 . Эту вероятность можно рассматривать как левую часть неравенства Маркова с
. Эту вероятность можно рассматривать как левую часть неравенства Маркова с 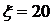 . Тогда
. Тогда
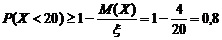 .
.
Пример. Сумма всех вкладов в некотором сберегательном банке составляет 2 млн. рублей, вероятность того, что случайно взятый вклад не превышает 10000 руб. равна 0.8. Что можно сказать о числе вкладчиков данного сберегательного банка?
Решение. Пусть 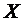 - величина случайно взятого вклада, а
- величина случайно взятого вклада, а 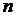 - число всех вкладчиков. Тогда из условия задачи следует, что
- число всех вкладчиков. Тогда из условия задачи следует, что 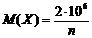 . Так как
. Так как 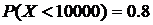 , то по неравенству Маркова получим
, то по неравенству Маркова получим 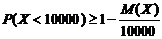 или
или
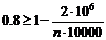 ,
, 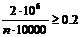 ,
, 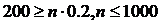 .
.
Неравенство Чебышева
Теорема. Каково бы ни было 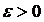 для любой случайной величины
для любой случайной величины 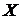 , дисперсия которой конечна, имеет место неравенство Чебышева
, дисперсия которой конечна, имеет место неравенство Чебышева
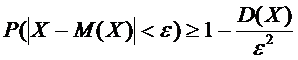 .
.
Доказательство. Рассмотрим величину 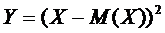 .
.
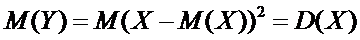 .
.
Для 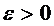 получим
получим
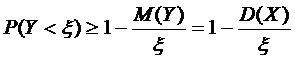 .
.
Подставим в это неравенство выражение 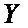 через
через 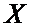 и
и 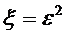
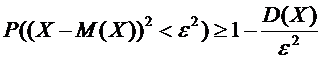 или
или
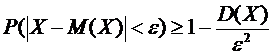
Примеры.
Определение.Последовательность чисел 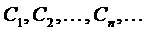 называется равномерно ограниченной, если существует такая постоянная М, что для любого
называется равномерно ограниченной, если существует такая постоянная М, что для любого 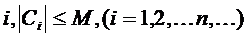 .
.
Теорема Чебышева
Если 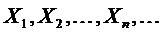 - последовательность попарно независимых случайных величин, у каждой из которых есть математическое ожидание
- последовательность попарно независимых случайных величин, у каждой из которых есть математическое ожидание 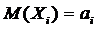 и дисперсия
и дисперсия 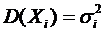 ,
, 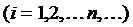 , причем дисперсии равномерно ограничены, то для любого положительного
, причем дисперсии равномерно ограничены, то для любого положительного 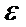
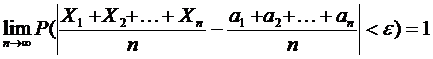
Доказательство.
Последовательность 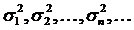 равномерно ограничена, т.е. существует такое М, что для любого натурального
равномерно ограничена, т.е. существует такое М, что для любого натурального 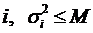 . Рассмотрим случайную величину
. Рассмотрим случайную величину
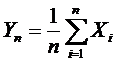 . У этой величины есть математическое ожидание и дисперсия:
. У этой величины есть математическое ожидание и дисперсия:
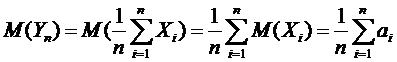 ,
,
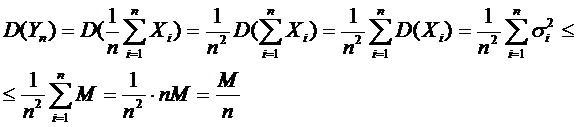
Здесь мы воспользовались свойством, что если случайные величины независимы, то дисперсия их суммы равна сумме их дисперсий.
Таким образом, 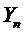 удовлетворяет всем требованиям для применения неравенства Чебышева, а значит, при любом
удовлетворяет всем требованиям для применения неравенства Чебышева, а значит, при любом 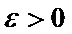 имеем
имеем
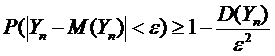 или
или
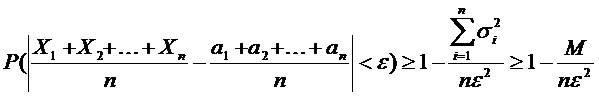
Итак,
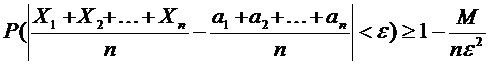
Пусть 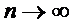 , тогда
, тогда 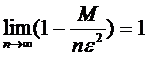 при любых
при любых 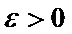 .
.
Отсюда 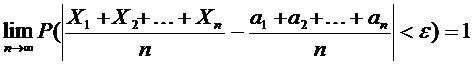 , что и требовалось доказать.
, что и требовалось доказать.
Следствие.
Если 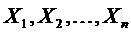 - последовательность независимых случайных величин, математические ожидания каждой из которых равны
- последовательность независимых случайных величин, математические ожидания каждой из которых равны 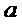 , а дисперсии
, а дисперсии 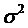 , то ……………
, то ……………
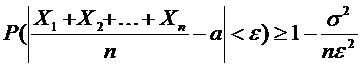
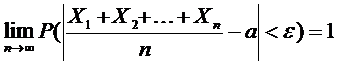
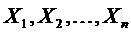
( 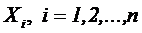 )
) 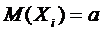
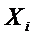
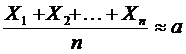
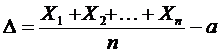
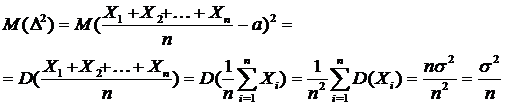
Отсюда следует 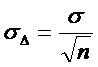 ,
,
Если точность всех измерений одна и та же, т.е. 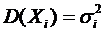 , i=1,2,…
, i=1,2,…
Теорема Бернулли
S n A p
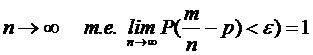
Пусть случайная величина 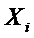 - число наступлений события А в i-ом испытании.
- число наступлений события А в i-ом испытании.
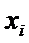 | ||
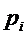 | 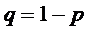 | 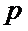 |
Следовательно,
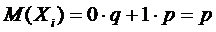
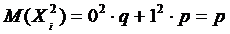
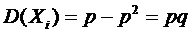
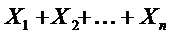 через m , то
через m , то
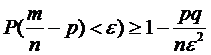 или
или 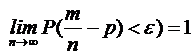
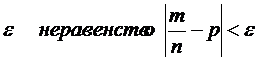
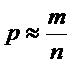
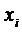
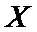
| i | … | ||||||
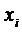 | … |
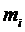
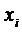 ,
, 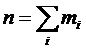
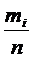
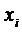
Теорема Ляпунова
Можно доказать, что CBX1X2…Xn –являются независим нормально распределенными CB, то сумма также распределена по номмальному закону с мат. Ожиданием равным сумме мат. ожиданий и дисперсией равной сумме дисперсий. Обобщением этого утверждения является следующая Т. Ляпунова
Т. Если X1X2…Xn –независимые CB, у каждой из которых существует мат ожидание и диспепсия 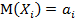 ,
, 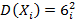 ,
, 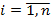 также существует
также существует 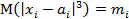 , а также
, а также
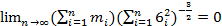 , тогда сумма S=X1+X2+…+Xn распределена асимптотически по нормальному закону с мат ожид равным сумме мат ожид и дисперсий равной сумме дисперсий, тогда для
, тогда сумма S=X1+X2+…+Xn распределена асимптотически по нормальному закону с мат ожид равным сумме мат ожид и дисперсий равной сумме дисперсий, тогда для 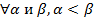
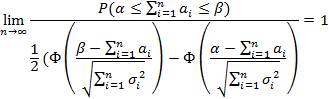
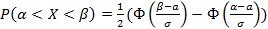 –ранее вывели. Ф-ция Лапласа.
–ранее вывели. Ф-ция Лапласа.
Следствием из Т. Липунова являются следующие неравенства:
1) 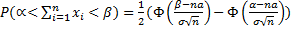
2) 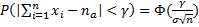
3) 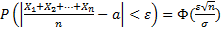
Здесь γ и ε –любые положительные числа, а также a1=a2=…=an=a, 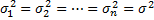
Например, если производятся измерения некоторой величины, истинное значение которой равно a, то среднее арифметическое значение результатов измерений отличается от истинного значения по модулю меньше чем ε с вероятностью прибл равной
