Определить корреляционную функцию этого процесса.

Решение. Пользуясь преобразованием Фурье, имеем

.

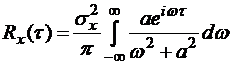Для вычисления этого интеграла применим теорию вычетов. При t > 0 интеграл 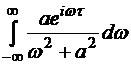равняется интегралу, взятому по контуру, составленному из вещественной оси и замкнутой полуокружности бесконечного радиуса, расположенной в верхней полуплоскости.

Поэтому его значение равно вычету относительно единственного полюса w = ia, умноженному на 2p a, т.е.

.

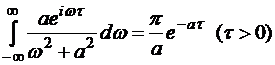Аналогично при t < 0, замыкая вещественную ось через нижнюю полуплоскость, получаем .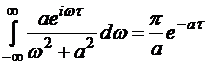

Следовательно, при любом знаке t получим: .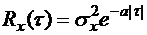

Пример 2.13. Найти корреляционную функцию стационарного случайного процесса X(t), если ее спектральная плотность 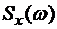постоянна на интервале 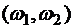и равна с, а вне этого интервала равна нулю:

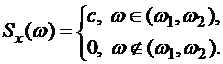
Решение. По определению корреляционной функции

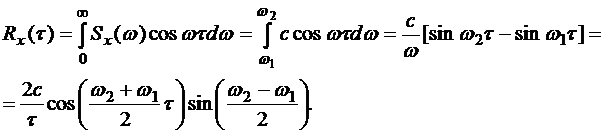
Дисперсия рассматриваемого случайного процесса X(t) будет

.

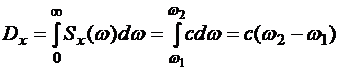Откуда .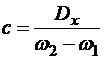

Следовательно,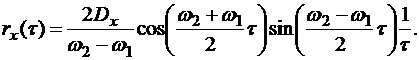

Рассмотрим предел этого выражения при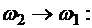

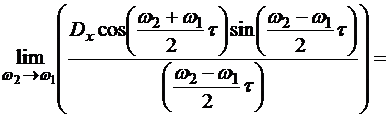
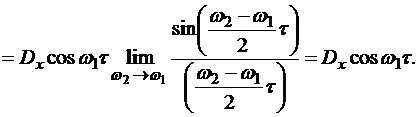
Таким образом, при мы получили случай, когда X(t) является элементарным стационарным случайным процессом – случайные колебания на частоте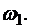

Пример 2.14. Найти спектральную плотность процесса X(t), представляющего собой случайную телеграфную волну с корреляционной функцией .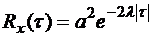

Решение.

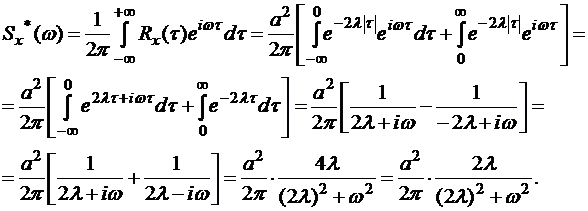
Пример 2.15. Показать, что не существует никакой стационарной случайной функции X(t), корреляционная функция которой 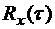постоянна в каком–то интервале (–t, t) и равна нулю вне его.

Решение. Предположим противное, т.е. что существует случайная функция X(t), для которой корреляционная функция равна значению b ¹ 0 при |t| < t₁ и равна 0 при |t| > t₁.

Попробуем найти спектральную плотность случайной функции X(t):

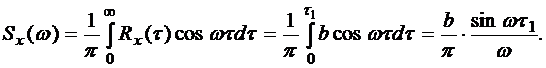
Из этого выражения видно, что функция 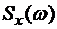для некоторых значений w отрицательна, что противоречит свойствам спектральной плотности, и следовательно, корреляционная функция указанного выше вида существовать не может.

Пример 2.16. Показать, что стационарный «белый шум» Х (t) имеет постоянную спектральную плотность.

Решение. У стационарного белого шума корреляционная функция может быть записана в виде 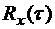= cd (t).

Отсюда

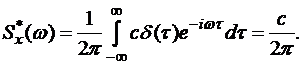
Величина с называется интенсивностью белого шума.

Таким образом, стационарный белый шум представляет собой случайные колебания на всех частотах.

При этом дисперсия этих колебаний, приходящихся на элементарный участок Dw, остается постоянной и не зависит от частоты колебаний w.

Эта дисперсия не зависит от частоты w и будет приближенно равна величине

.

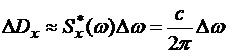Пример 2.17.

Система описывается диф. уравнением:

.

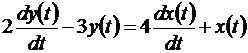Найти частотные характеристики системы.

Решение. Найдем передаточную функцию системы:

.

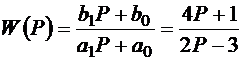Амплитудно–фазовая функция системы: .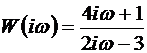

Выражение для амплитудной частотной характеристики найдем как отношение модулей:

.

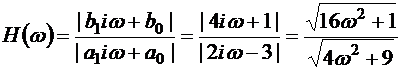а для фазовой частотной характеристики – как разность аргументов числителя и знаменателя:

.

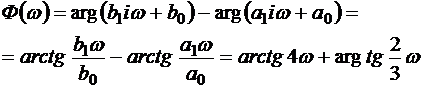Пример 2.18. Найти переходную функцию 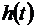элемента, описываемого уравнением .

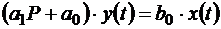Решение. Переходная функция имеет две составляющие:

.

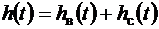Вынужденная составляющая в данном случае равна:

.

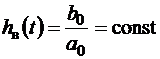Свободную составляющую будем искать в виде:

.

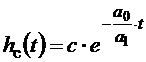Учитывая начальное условие 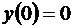, получим: .

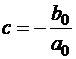Тогда .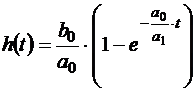

Пример 2.19.

Определить реакцию элемента, описываемого уравнением 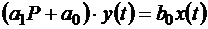, на воздействие .

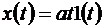Решение.

Импульсная переходная функция элемента:

.

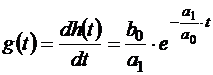Функцию 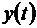, описывающую изменение выходной величины после подачи линейного воздействия, получим, подставляя последнее выражение в интеграл Дюамеля:

.
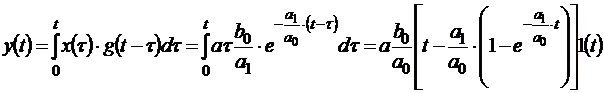