Свойства производной по направлению.

1. Производная по направлению имеет наибольшее значениепо направлению градиента, что следует из коллинеарности 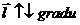, то есть cos 0 = 1 и .
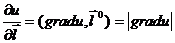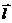
2. Производная по направлению равна нулю по направлению, перпендикулярному градиенту, что следует из ортогональности 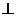gradu, то есть cos (π/2) = 0 и .

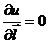Замечания. 1) Другие обозначения градиента функции:

gradu = gru = 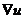, где вектор 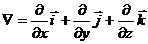называется оператор Гамильтона или оператор набла.

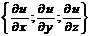Тогда 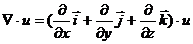= = 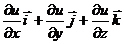– разные формы записи градиента.

1) 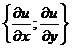Если функция u = u(x,y) 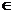R⁽²⁾, то градиент функции – это вектор = = ,

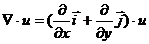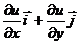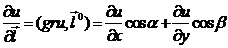а производная по направлению – число, равное .

Пример 3.Найти производную функции u = x² + y² + z² по

направлению вектора 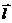= {2;1;-2} в точке М(1;1;1).

Производную функции u = x² + y² + z² по направлению вектора

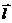={2;1;-2}

найдем по определению .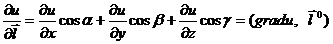

Вычислим градиент gradu= 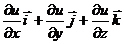= {2x; 2y; 2z} в произвольной точке, а затем в точке М(1;1;1): gradu(М) = {2; 2; 2}.

Нормируем вектор 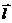= {2;1;-2}.

Для этого найдем его длину 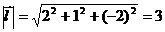и координаты единичного вектора 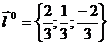, где cosα = 2/3; cosβ= 1/3; cosγ = – 2/3/

.

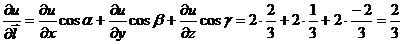Билет №44. Касательная к плоскости и нормаль к поверхности.

Пусть имеется поверхность, заданная уравнением 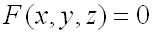. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку 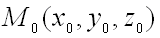, называется касательной плоскостью к поверхности в точке .

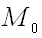Прямая, проведенная через точку 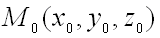поверхности 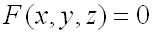, перпендикулярно к касательной плоскости называется нормалью к поверхности.

Если поверхность задана уравнением 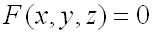, то уравнение касательной плоскости к этой поверхности в точке 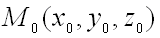записывается в виде:
,
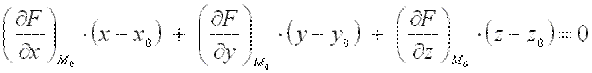а уравнение нормали к поверхности в этой же точке – в виде:

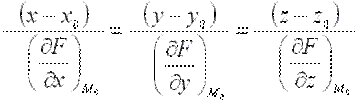
Примеры решения задач

Пример 1. Найти уравнение касательной плоскости и нормали к поверхности 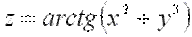в точке .

Решение.

Уравнение касательной плоскости к поверхности, заданной уравнением 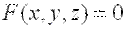, в точке 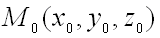записывается в виде: .

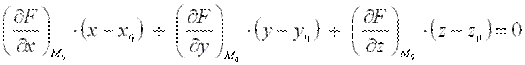Так как в условии задачи уравнение поверхности задано в явном виде, то сначала его необходимо преобразовать к виду : .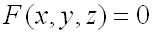

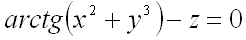Теперь найдем частные производные 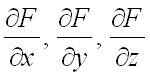(при этом, в первых двух случаях используем правило дифференцирования сложной функции одной переменной):

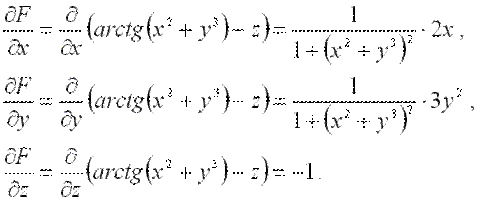
Вычислим значения частных производных первого порядка в точке :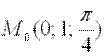

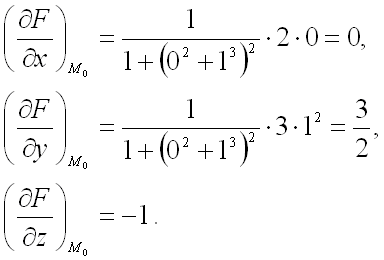
Подставим полученные значения в уравнение касательной плоскости:

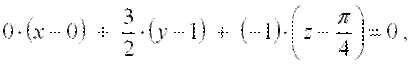
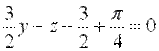
Как известно, уравнение нормали к поверхности, заданной уравнением 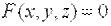, в точке 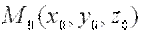записывается в виде: .

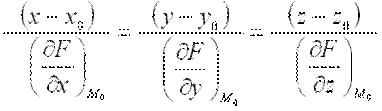Поскольку нормаль к поверхности есть (по определению) прямая линия, а в каноническом уравнении прямой числа, стоящие в знаменателях дробей, суть – координаты направляющего вектора этой прямой, то равенство нулю знаменателя первой дроби – 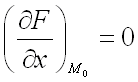, означает, что данная прямая лежит в плоскости, перпендикулярной оси 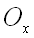, и первые координаты всех точек этой прямой совпадают между собой и равны первой координате точки 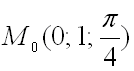, так как по условию через нее проходит нормаль к поверхности.

Таким образом, уравнение нормали к поверхности, заданной уравнением 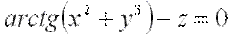, в точке 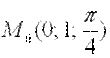записывается в виде:

Ответ: 1) 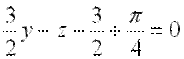– уравнение касательной плоскости к поверхности 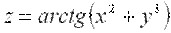в точке ;
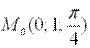2) 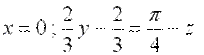– уравнение нормали к этой поверхности в той же точке.

· Говорят, что функция 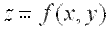имеет максимум в точке 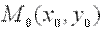, т.е. при 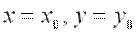, если 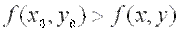для всех точек 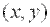, достаточно близких к точке 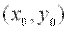и отличных от неё.

· Говорят, что функция 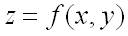имеет минимум в точке 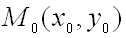, т.е. при 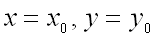, если 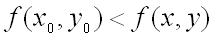для всех точек 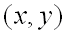, достаточно близких к точке 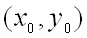и отличных от неё.

Максимум и минимум функции называются экстремумами функции.

Билет №45. Теорема (необходимое условие экстремума функции двух переменных)

Если функция 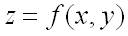достигает экстремума при 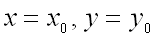, то каждая частная производная первого порядка от 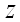или обращается в нуль при этих значениях аргументов, или не существует.

Билет №46. Теорема (достаточное условие экстремума функции двух переменных)

Пусть в некоторой области, содержащей точку 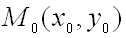функция 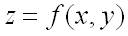имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка 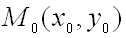является критической точкой функции 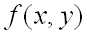, т.е.
,
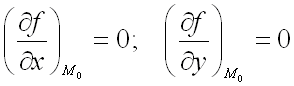тогда при :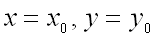
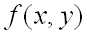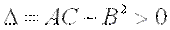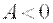1) имеет максимум, если дискриминант и , где ;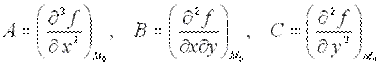
2) 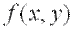имеет минимум, если дискриминант 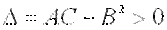и ;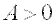
3) 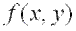не имеет ни минимума, ни максимума, если дискриминант ;
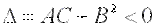4) если 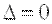, то экстремум может быть, а может и не быть (требуется дополнительное исследование).