Практическая работа. уравнения и неравенства с одной переменной.

Цель.Углубить знания о числовых неравенствах и равенствах. Раскрыть трактовку понятий равенства и неравенства в начальном курсе математики.

Теоретическая часть

Вопросы к изучению

1. Уравнения с одной переменной.

2. Теоремы о равносильности уравнений с одной переменной.

3. Неравенства с одной переменной.

4. Теоремы о равносильности неравенств с одной переменной.

Основные понятия темы

Ø уравнение с одной переменной;

Ø корень уравнения;

Ø что значит решить уравнение;

Ø равносильные уравнения;

Ø неравенство с одной переменной;

Ø решение неравенства;

Ø что значит решить неравенство;

Ø равносильные неравенства.

Замечания, выводы

Ø рассмотрены теоремы о равносильности уравнений и неравенств, являющиеся основой их решения.

Ø Знание определений всех названных выше понятий и теорем о рав­носильности уравнений и неравенств - необходимое условие методи­чески грамотного изучения с младшими школьниками алгебраическо­го материала.

Практическая часть

1. Установите, какие из следующих записей являются уравнениями с одной переменной:

а) (х-3) × 5= 12х; г) 3+(12-7) × 5 = 16;

б) (х-3) × 5= 12; д) (х-3) × у =12х;

в) (х-3) × 17+ 12; е) х² - 2х + 5 = 0.

2. Уравнение 2х⁴ + 4х² -6=0 задано на множестве натуральных чисел. Объясните, почему число 1 является корнем этого уравнения, а 2 и -1 не являются его корнями.

3. В уравнении (х + ...)(2х + 5) - (х - 3)(2х + 1) = 20 одно число стерто и заменено точками. Найдите стертое число, если известно, что корнем этого уравнения является число 2.

4. Сформулируйте условия, при которых: а) число 5 является корнем уравнения f(х) = q(х); б) число 7 не является корнем уравнения f(х) = q(х).

5. Установите, какие из следующих пар уравнений равносильны на множестве действительных чисел:

а) 3+7х= - 4 и 2(3+7х)= - 8; б) 3+7х = - 4 и 6+7х = - 1; в) 3+7х = - 4 и х + 2=0.

6. Сформулируйте свойства отношения равносильности уравнений. Какие из них используются в процессе решения уравнения?

7. Решите уравнения (все они заданы на множестве действительных чисел) и обоснуйте все преобразования, выполняемые в процессе их упрощения:

а) 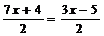; б) х - 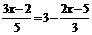; в) (2 – х) 2 – х ( х – 1,5) = 4.

8. Учащийся решил уравнение 5х + 15 = 3х + 9 следующим обра­зом: вынес за скобки в левой части число 5, а в правой число 3, полу­чил уравнение 5(х + 3) = 3(х + 3), а затем разделил обе части на выражение х + 3. Получил равенство 5 = 3 и сделал вывод – данное уравнение корней не имеет. Прав ли учащийся?

9. Решите уравнение 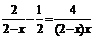; х ÎR. Является ли число 2 корнем этого уравнения?

10. Решите уравнения, используя взаимосвязь между компонентами и результатами действий:

а) (х + 70) • 4 = 328; в) (85х + 765): 170 = 98;

б) 560 : (х + 9) = 56; г) (х - 13581): 709 = 306.

11. Решите задачи арифметическим и алгебраическим способами:

а) На первой полке на 16 книг больше, чем на второй. Если с каж­дой полки снять по 3 книги, то на первой полке книг будет в полтора раза больше, чем на второй. Сколько книг на каждой полке?

б) Весь путь от турбазы до станции, равный 26 км, велосипедист проехал за 1 ч 10 мин. Первые 40 мин этого времени он ехал с одной скоростью, а остальное время - со скоростью на 3 км/ч меньше. Най­дите скорость велосипедиста на первом участке пути.

12. Установите, какие из следующих записей являются неравенства­ми с одной переменной:

а) - 12 - 7х < 3х + 8; г) 12х + 3(х- 2);

б) 15(х + 2) > 4; д) 17-12 × 8;

в) 17× (13+8)< 14 - 9; е) 2х² + 3х – 4 > 0.

13. Является ли число 3 решением неравенства 6 (2х + 7) < 15(х + 2), х ÎR? А число 4,25?

14. Равносильны ли на множестве действительных чисел следующие пары неравенств:

а)-17х < -51 и х > 3; б) 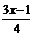> 0 и 3х – 1 >0; в) 6 - 5х > - 4 и х < 2?

15. Какие из следующих высказываний истинны: а) -7х < -28 Þ х > 4; б) х < 6 Þ х < 5; в) х < 6 Þ х < 20?

16. Решите неравенство 3(х - 2) - 4(х + 1) < 2 (х - 3) - 2 и обоснуйте все преобразования, которые будете при этом выполнять.

17. Докажите, что решением неравенства 2 (х +1) + 5 > 3 - (1-2х) является любое действительное число.

18. Докажите, что не существует действительного числа, которое являлось бы решением неравенства 3(2 - х)-2 > 5- 3х.

19. Одна сторона треугольника равна 5 см, а другая 8 см. Какой может быть длина третьей стороны, если периметр треугольника: а) меньше 22 см; б) больше 17 см?

Творческие задания

1. Решите задачу различными алгебраическими способами: «От деревни до совхоза 20 км, а от совхоза до станции 40 км. Из совхоза по направлению к станции выехал велосипедист со скоростью 12 км/час. Одновременно на станцию через совхоз по той же дороге отправился мотоциклист. С какой скоростью должен ехать мотоциклист, чтобы догнать велосипедиста до его приезда на станцию?».

2. Решите задачу алгебраическим и арифметическим методом: «В двух пачках всего 30 тетрадей, Если бы из первой пачки переложили во вторую 2 тетради, то в первой пачке стало бы вдвое больше тетрадей, чем в первой. Сколько тетрадей было в каждой пачке?».

3. Решите задачу алгебраически и проверьте, решив арифметически: «Из пункта А выехал велосипедист. Одновременно вслед за ним из пункта В, отстоящего от А на 20 км, выехал мотоциклист. Велосипедист ехал со скоростью 12 км/час, а мотоциклист со скорость. 16 км/час. на каком расстоянии от пункта А догонит мотоциклист велосипедиста?».

4. Решите задачу арифметическим методом и проверьте, решив ее алгебраическим: «В двух кусках одинаковое количество тканей. После того как от одного куска отрезали 18 м, а от другого 25 м, в первом куске осталось вдвое больше ткани, чем во вто­ром. Сколько метров ткани было в каждом куске?».

5. Решите задачу алгебраическим методом. Что в условии задачи явилось обоснованием к составлению уравнения? Бригада рабочих должна была за определенный срок изготовить 400 деталей. В течение 5 дней бригада перевыполнила дневную норму на 20 %, а в последующие дни изготовляла ежедневно по 15 деталей сверх плана и уже за два дня до срока из­готовила 405 деталей. Сколько деталей должна была изготовлять ежедневно бригада по плану?

6. Решите задачу. Какой метод решения задачи выбрали? Как выполнили проверку решения задачи? Группа туристов отправилась на экскурсию из города А в город В на пароходе, а воз­вратилась обратно по железной дороге. Расстояние от А до В по воде 96 км, а по железной дороге 72 км. Поезда по железной дороге продолжалась на 2 час. 40 мин. меньше, чем на пароходе. Средняя скорость парохода на 30 км/час меньше скорость поезда. Какова скорость движения парохода и поезда?

7. Составьте текстовые задачи по математической модели.

а) 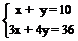; b) .

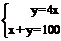8. Составьте текстовые задачи, математической моделью которых являются неравенства: а) х + 5 £ 10; б) х + 5 ³ 5. Составленные задачи решите арифметически, алгебраически и графически. Сколько решений имеют составленные задачи?

9. Составьте текстовые задачи, моделью которых являются системы уравнений:

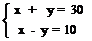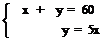а) ; b) ; c)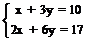

Составленные задачи решите арифметически, алгебраически и графически. Какие величины рассматриваются в задачах?