Неравенства с одной переменной
Предложения 2х+7>10-х, х2+7х<2, (х+2)(2х-3)> 0 называют неравенствами с одной переменной.
В общем виде это понятие определяют так:
Определение.Пусть f(х) и q(х) - два выражения с переменной х и областью определения X. Тогда неравенство вида f(х) < q(х) или f(х) > q(х) называется неравенством с одной переменной. Множество Х называется областью его определения.
Значение переменной х из множества X, при котором неравенство обращается в истинное числовое неравенство, называется его решением.Решить неравенство - это значит найти множество его решений.
Так, решением неравенства 2х +7>10-х, х Î R является число х=5, так как 2×5+7>10-5- истинное числовое неравенство. А множество его решений - это промежуток (1, ¥), который находят, выполняя преобразование неравенства: 2х+7>10-х Þ 3х> Þ х>1.
В основе решения неравенств с одной переменной лежит понятие равносильности.
Определение.Два неравенства называются равносильными, если их множества решений равны.
Например, неравенства 2х+7>10 и 2х>3 равносильны, так как их множества решений равны и представляют собой промежуток 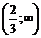
Теоремы о равносильности неравенств и следствия из них аналогичны соответствующим теоремам о равносильности уравнений. При их доказательстве используется свойства истинных числовых неравенств.
Теорема 3. Пусть неравенство f(х) > q(х) задано на множестве Х и h(х) - выражение, определенное на том же множестве. Тогда неравенства f(х) > q(х) и f(х)+ h(х) > q(х)+ h(х) равносильны на множестве X.
Из этой теоремы вытекают следствия, которые часто используются при решении неравенств:
1) Если к обеим частям неравенства f(х) > q(х) прибавить одно и то же число d, то получим неравенство f(х)+ d > q(х)+ d, равносильное исходному.
2) Если какое-либо слагаемое (числовое выражение или выражение с переменной) перенести из одной части неравенства в другую, поменяв знак слагаемого на противоположный, то получим неравенство, равносильное данному.
Теорема 4. Пусть неравенство f(х) > q(х) задано на множестве Х и h(х) - выражение, определенное на том же множестве, и для всех х из множества Х выражение h(х) принимает положительные значения. Тогда неравенства f(х)× h(х) > q(х)× h(х) равносильны на множестве X.
Из этой теоремы вытекает следствие: если обе части неравенства f(х) > q(х)умножить на одно и то же положительное число d, то получим неравенство f(х)× d > q(х)× d , равносильное данному.
Теорема 5. Пусть неравенство f(х) > q(х) задано на множестве Х и h(х) - выражение, определенное на том же множестве, и для всех х их множества Х выражение h(х) принимает отрицательные значения. Тогда неравенства f(х) > q(х) b f(х)× h(х) < q(х)× h(х) равносильны на множестве X.
Из этой теоремы вытекает следствие: если обе части неравенства f(х) > q(х)умножить на одно и то же отрицательное число d и знак неравенства поменять на противоположный, то получим неравенство f(х)× d < q(х) × d, равносильное данному.
Решим неравенство 5х - 5 < 2х - 16,х Î R ,и обоснуем все преобразования, которые мы будем выполнять в процессе решения.
| Преобразования | Обоснование преобразований |
| 1. Перенесем выражение 2х в левую часть, а число – 5 в правую, поменяв их знаки на противоположные: 5х – 2х < 16 + 5 | Воспользовались следствием 2 из теоремы 3, получили неравенство, равносильное исходному. |
| 2. Приведем подобные члены в левой и правой частях неравенства: 3х < 21. | Выполнили тождественные преобразования выражений в левой и правой частях неравенства – они не нарушили равносильности неравенств: данного и исходного. |
| 3. Разделим обе части неравенства на 3: х < 7. | Воспользовались следствием из теоремы 4, получили неравенство, равносильное исходному. |
Решением неравенства х < 7 является промежуток (- ¥, 7) и, следовательно, множеством решений неравенства 5х - 5 < 1х + 16 является промежуток (- ¥, 7).
ПРАКТИЧЕСКАЯ РАБОТА. ВЫРАЖЕНИЯ И ИХ ПРЕОБРАЗОВАНИЯ. ЧИСЛОВЫЕ РАВЕНСТВА И НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ.
Цель. Уточнить и углубить знания о выражениях (числовых и с переменными), о числовых неравенствах и равенствах.
Теоретическая часть
Вопросы к изучению
1. Алфавит математического языка.
2. Выражения (числовые и с переменными), их тождественные преобразования.
3. Числовые равенства и неравенства, их свойства.
Основные понятия темы
Ø числовое выражение;
Ø значение числового выражения;
Ø выражение, не имеющее смысла;
Ø выражение с переменной (переменными);
Ø область определения выражения;
Ø тождественно равные выражения;
Ø тождество;
Ø тождественное преобразование выражения.
Ø числовое равенство;
Ø числовое неравенство
Практическая часть
Обязательные задания
1. Среди следующих записей укажите числовые выражения: а) 42: 5; б) 27; в) 32 + - ) : 14; г) 2 × 7 = 7 × 2; д) (17 + 130 : 10 – 15; е) 142 > 71 × 2.
2. Какие из следующих выражений имеют смысл, если рассматривать их на множестве натуральных чисел: а) (135+67) × 12; б) (135 - 217):2; в) 362 : 4?
3. Какие из нижеприведенных записей являются выражениями с переменными: а) 8 + 0,3b; б) 21 – (4 + у); в) х + 2у < 7; г) 32 : у + 3 = 5у?
4. Установите, какая область определения выражений, если рассматривать их на множестве действительных чисел: а) (3 – у) : 64; б) 64 : (3 – у); в) (5 + х) : ( х – 12).
5. Известно, что выражение называется по своему последнему действию. Укажите порядок действий и дайте название каждому выражению:
| Выражение | Название выражения |
| (12 × 5 + 3 : (2 + 7 ) ) × 18 | |
| (23 – 7 × 6 – 4 + 15) : (17 – 6) | |
| 21 + (35 × 3 : 8- 14 :5) | |
| 19 – 8 : 4 +5 |
6. Вычислите значение выражения: а) ((36 : 2 – 14) × (42 × 2 – 14) + 20) : 2; б) (72 : 12 – (18 – 15)) : (24 : 3 – 2 × 4); в) (16,583 : 7,21 + 54,68 × 853,2 + 28,82 × 0,1) : 1, 6 – 1,02.
7. Выясните, являются ли выражения 3 (4 - х) и 12 – 3х тождественно равными на множестве: а) {1, 2, 3, 4}; б) действительных чисел.
8. Какие из следующих равенств являются тождествами на множестве действительных чисел: а) 3р + 5а = 5а + 3р; в) 3р × 5а = 5а × 3р; б) 3р – 5а = 5 а -3р; г) 3р : 5а = 5а : 3р?
9. Обоснуйте каждый шаг в преобразованиях следующих выражений: а) 324×5 =(300+20+4)×5= 300×5+20×5+4×5= 1500+100+20 = 1500+120 = 1620; б)97×12 =(100 - 3) ×12= 100×12-3×12= 1200-36= 1100+(100-36)= 1164; в) 5 (1-2х)+ 10х = 5-10х+ 10х = 5.
10. Объясните, почему отношение «иметь одно и то же значение на множестве числовых выражений является отношением эквивалентности. Какие следствия из этого факта используются при выполнении тождественных преобразований числовых выражений?
11. Упростите выражение путем тождественных преобразований: а) 6 (2аb-3)+2а (6b-5); б) (12а-16b):4 - (10а-4b).
12. Сравните значения выражений, не выполняя действий: а) (30+56) × 5 и 30×5+56×5; б) (19+4) × 7 и 19×7+10×7; в) (14-7) × 6 и 16 × 6 - 7×6; г) (18 - 9) ×7 и 18 × 7 – 11 × 7.
13. Решите задачу; решение запишите в виде выражения:
а) На туристическую базу прибыли в один день 150 туристов, другой день 170. Чтобы пойти по маршрутам, 200 туристов разбились на группы, по 20 человек в каждой, а остальные по 15 человек в группе. Сколько получилось групп?
б) В мастерской за 5 дней сшили 2000 фартуков. Сколько фартуков сошьют за 8 дней, если будут шить в день на 50 фартуков больше?
в) Слесарь обработал 6 деталей. Первую деталь он обрабатывал 18 мин, а каждую следующую на 3 мин быстрее, чем предыдущую. Сколько минут потребовалось для обработки всех деталей?
13. Установите, какие из следующих числовых равенств и неравенств истинны:
а) 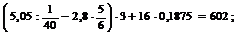
б) 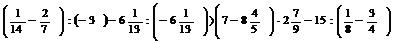
в) 1, 0905 : 0,025 – 6,84 × 3,07 + 2,38 : 100 < 4, 8 : (0,04 × 0,006).
14. Проверьте, истинны ли числовые равенства: 13×93 = 31×39,14×82 = = 41×28, 23×64 = 32×46. Можно ли утверждать, что произведение любых двух натуральных чисел не изменится, если в каждом множителе переставить цифры?
15. Известно, что х > у - истинное неравенство. Будут ли истинными следующие неравенства:
а) 2х > 2у; в) 2х – 7 < 2у – 7;
б) - 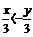 ; г) – 2х – 7 < - 2у – 7 ?
; г) – 2х – 7 < - 2у – 7 ?
16. Известно, что а < b - истинное неравенство. Поставьте вместо * знак «>» или «<» так, чтобы получилось истинное неравенство:
а) – 3,7 а * - 3,7 b; г) _ 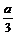 * -
* - 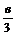 ;
;
б) 0,12 а * 0,12 b; д)-2(а+5) * -2(b+5);
в) 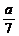 *
* 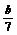 ; е)
; е) 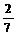 (а-1) *
(а-1) * 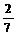 (b-1)
(b-1)
17. Дано неравенство 5 > 3. Умножьте обе его части на 7; 0,1; 2,6; 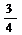 .
.
Можно ли на основании полученных результатов утверждать, что для любого положительного числа а неравенство 5а > 3а истинно?
18. Выполните задания, которые предназначаются ученикам начальных классов, и сделайте вывод о том, как трактуются в начальном курсе математики понятия числового равенства и числового неравенства:
а) Запиши два верных равенства и два верных неравенства, используя выражения: 9 × 3, 30 - 6, 3 × 9, 30 - 3. б) Расставь скобки так, чтобы равенства были верными: 4 + 2 × 3 = 18; 31-10-3=24; 54-12+8=34. в) Поставь вместо * знаки действий так, чтобы получились верные равенства: 3*6*2=9; 9*3*6=18.
Творческие задания
1. Какие ответы учеников вы будете считать правильными при выполнении ими задания - сравнить выражения, не вычисляя их значения: а) 70 × 32+9 × 32...79×30+79×2; б)7 × 4+3 × 4...(7+8) × 4; в) 8500:1700 ...8500:100:17; г) 24 × 6080 ...(6000+80) × 24?
2. Составьте текстовую задачу, решение которой можно оформить в виде числового выражения (12 + 9) ´ 4. Сколькими арифметическими способами можно решить эту задачу? Какова теоретическая основа разных способов арифметического решения этой задачи?
3. Составьте текстовые задачи, математическая модель которых: а) 17 ´ 3; б) (5 + 7 ) ´ 8; в) (25 + 43) ´ 3.
4. Составьте текстовые задачи, математическая модель которых: а) 35 : 7; б) (21 + 18) : 3; в) (1 + 14) : 3.
