Тема 6: Экономические индексы.

Индивидуальный индекс цены рассчитывается по формуле: 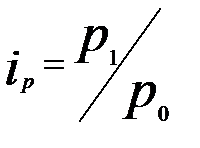, где

р₁ – цена товара в текущем периоде;

р₀ – цена товара в базисном периоде.

Например, если цена товара А в текущем периоде составляла 30 руб., а в базисном 25 руб., то индивидуальный индекс цены : i_р = 30 /25 = 1,2 или 120,0 %.

В данном примере цена товара А возросла по сравнению с базисным уровнем в 1,2 раза, или на 20 %.

Индивидуальный индекс физического объема реализации: 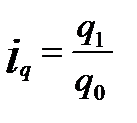, где

q₁ – количество товара, реализованное в текущем периоде,

q₀ – количество товара, реализованное в базисном периоде.

Индивидуальный индекс товарооборота: .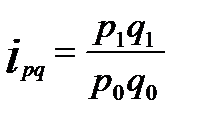

Сводный индекс товарооборота:Сводный индекс цен по методу Пааше:

.

,

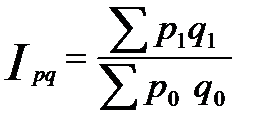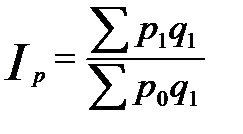
В данном случае фиксируется количество проданного товара на текущем уровне.

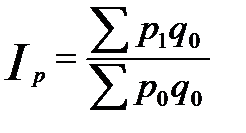- сводный индекс цен по методу Ласпейреса, здесь фиксируется количество проданного товара на базисном уровне. В случае, когда не указано, по какому методу рассчитать сводный индекс цен, его рассчитывают по методу Пааше.

Сводный индекс физического объема реализации.

.

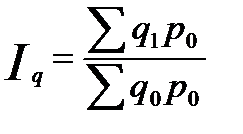Разность числителя и знаменателя сводного индекса цен будет отражать величину экономии (если знак "-") или перерасхода ("+") покупателей от изменения цен: Е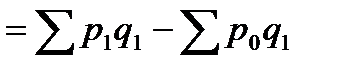

Между данными индексами существует следующая взаимосвязь:

.

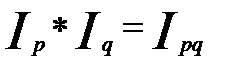Пример. Имеются следующие данные о реализации плодово-ягодной продукции в области:

Наименование товара	Июль	Август	Расчетные графы, руб.
Цена за 1 кг., руб. p0	Продано, т q0	Цена за 1 кг., руб. р1	Продано, т q1	p0q0	p1q1	p0q1
Черешня
Персики
Виноград
Итого	х	х	х	х

Рассчитать индекс товарооборота.

Решение.

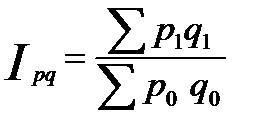= 618/ 638 = 0,969, или 96,9 %.

Мы получили, что товарооборот в целом по данной товарной группе в текущем периоде по сравнению с базисным уменьшился на 3.1 % (100 – 96.9). Отметим, что объем товарной группы при расчете этого и последующих индексов значения не имеет. Вычислим сводный индекс цен: 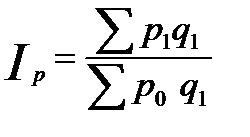= 618 / 693 = 0,892, или 89,2 %.

Т.о. по данной товарной группе цены в августе по сравнению с июлем в среднем снизились на 10,8 %.

Числитель и знаменатель сводного индекса цен можно интерпретировать с точки зрения потребителей. Числитель представляет собой сумму денег, фактически уплаченных покупателями за приобретенные в текущем периоде товары. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились. Разность числителя и знаменателя будет отражать величину экономии (если знак "-") или перерасхода ("+") покупателей от изменения цен: Е 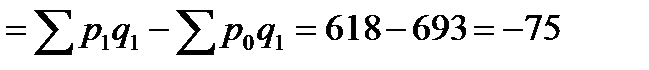тыс. руб.

Индекс физического объема реализации составит:

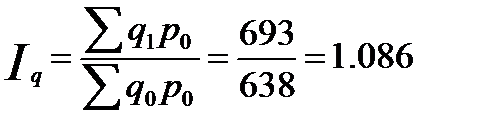, или 108,6 %.

Физический объем реализации (товарооборота) увеличился на 8,6 %.

Используя взаимосвязь индексов, проверим правильность вычислений:

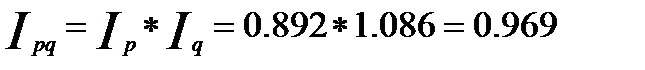, или 96,9 %.

Следующая группа индексов включает индексы затрат на производство, себестоимости и физического объема продукции, которые представлены ниже соответственно:

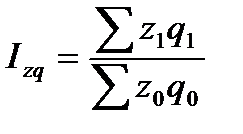
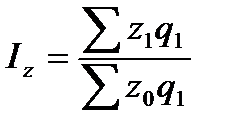
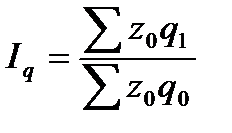
где z₁ и z₀ - себестоимость продукции в текущем и базисном периоде соответственно;

q₁ и q₀– количество продукции, произведенное в текущем и базисном периоде.

Разность числителя и знаменателя сводного индекса себестоимости показывает сумму экономии предприятия от снижения себестоимости: Е = Σz₁q₁ - Σ z₀q₁

Между данными индексами существует следующая взаимосвязь:

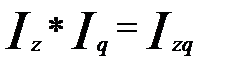
В зависимости от условий применения средний арифметический или средний гармонический индексы, тождественные агрегатной форме индекса. Индексы качественных показателей (цен, себестоимости и др.) определяются по средней гармонической из индивидуальных индексов. Так, агрегатный индекс цен преобразуется в среднегармонический индекс цен:

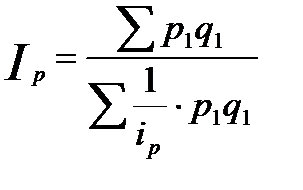
Индексы объемных, количественных показателей (физического объема реализации, продукции и др.) определяются по средней арифметической из индивидуальных индексов. Так, агрегатный индекс количества реализованных товаров преобразуется в среднеарифметический индекс:

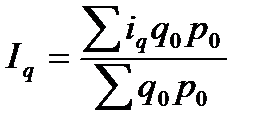
Пример.

По данным таблицы получить сводную оценку изменения цен.