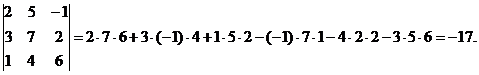Основные операции матричной алгебры

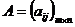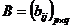1. Равенство матриц. Две матрицы и называются равными, если они имеют одинаковый размер (m = p и n = q) и равны их соответствующие элементы, т.е.:

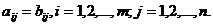(7)

2. Сумма матриц. Суммой А+В двух матриц 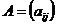и 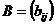одинакового размера mxn называется матрица 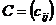того же размера, элементы которой равны сумме соответствующих элементов слагаемых матриц, т.е.:

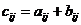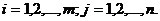, (8)

Формула (8) означает, что сложение матриц происходит поэлементно.

Например. Найти сумму двух матриц.

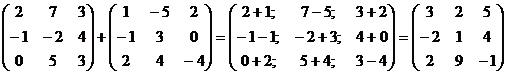
Для матриц справедливы сочетательный и переместительный законы сложения:

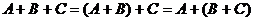(сочетательный закон)

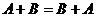(переместительный закон)

3. Разность двух матрицопределяется аналогично сумме:

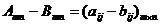(9)

Имеют место равенства:

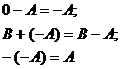
4. Произведение матрицы на действительное число.Произведением матрицы 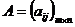на число k называется матрица того же размера, все элементы которой равны произведению соответствующих элементов матрицы А на число k, т.е.:

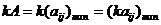(10)

Так же, как и сложение матриц, умножение матрицы на число происходит поэлементно.

Например. Умножить матрицу на число.

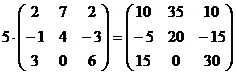
Умножение матрицы на число подчиняется правилам:

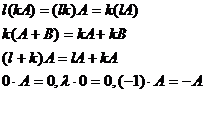
5. Произведение матриц.Произведением матрицы 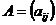размера mxn на матрицу 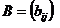размера nxq называется матрица 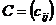размера mxq, элементы которой определяются по формуле:

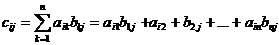, I = 1,2,…,m; j = 1,2,…q. (11)

т.е. элемент 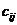равен сумме произведений элементов i – ой строки матрицы А на соответствующие элементы j – го столбца матрицы В.

Замечания:

1. Две матрицы 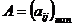и 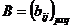можно перемножить только в том случае, если число столбцов матрицы А равно числу строк матрицы В, т.е. АВ можно вычислить, если n = p (ВА можно вычислить, если q = m). Другими словами говорят, что форма матриц А и В должна быть согласованной, а такие матрицы называют сцепленными.

2. Из сказанного выше следует, что, если существует АВ, то из этого не следует существования ВА, а, если ВА существует, то АВ ¹ВА.

3. Сложение и умножение матриц связаны дистрибутивными законами, т.е.

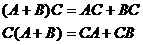
Пример 1. Вычислить произведения матриц.

a) Дано: 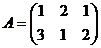, 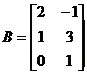. Найти АВ и ВА.

Решение.

=

= =

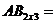
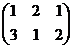
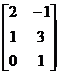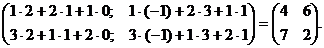
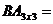
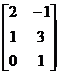
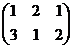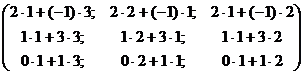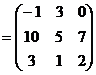
Пример показывает, что АВ ¹ ВА, т.е. умножение матриц не обладает переместительным свойством.

b) Дано: 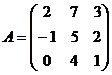, 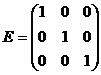. Найти АЕ.

Решение.

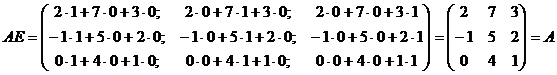
Итак, АЕ = А, т.е. единичная матрица Е ведет себя как число 1.

c) Дано: 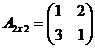, 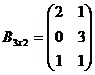. Найти АВ и ВА.

Решение.

Произведение АВ не имеет смысла, т.к. n ¹ p, но ВА можно вычислить, т.к. q = m.

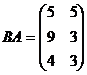
6. Транспонированная матрица.Если в данной матрице А размером mxn поменять местами строки и столбцы, то полученную матрицу размером nxm обозначают 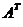(или 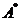) и называют транспонированной по отношению к данной. Или: матрица 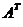называется транспонированной к матрице А, если выполняется условие:

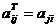для всех i и j. (12)

Пример 2.Транспонировать матрицу: .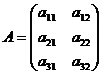

Решение.

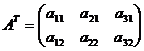
Замечания:

– квадратная матрица 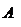называется симметричной, если = ;

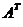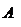– квадратная матрица называется кососимметричной, если = – ;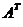

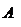– любую матрицу А можно представить (единственным образом) в виде А = В + С, где В – симметричная, С – кососимметричная матрицы.

ОПРЕДЕЛИТЕЛИ

Понятие определителя

Понятие "определитель" впервые было введено Г.Лейбницем при решении систем линейных уравнений (1693г.). В 1750 г. метод определителей был вновь разработан Г.Крамером, затем дополнен А.Вандермондом (1772г.). Термин "определитель" в современном его значении ввел О.Коши (1815 г.), а обозначения – вертикальные линии – А.Кели.

Приложения определителей:

- математика (векторная алгебра, аналитическая геометрия, линейная алгебра…)

- электротехника (расчет электрических цепей…)

- физика.

Каждой квадратной матрице А порядка n можно однозначно поставить в соответствие число, которое называется определителем (детерминантом) матрицы А и обозначается:

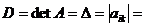
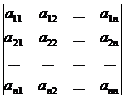(1)

По определению определитель n-го порядка матрицы А равен алгебраической сумме n! произведений, в каждое из которых входит только по одному элементу из каждой строки и каждого столбца матрицы А.

Вычисление определителей

Определители 2-го порядка

Определение. Определителем второго порядка называется число,вычисляемое по формуле:

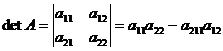. (2)

Мнемоническое правило для вычисления определителей 2-го порядка: определитель равен произведению главных диагональных элементов минус произведение побочных диагональных элементов.

Приведенное правило можно проиллюстрировать рисунком:

– +

Пример 1.

1. Вычислить определитель: .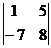

Решение:

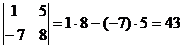
2. Решить уравнение: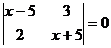

Решение:

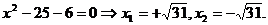
Определители 3-го порядка

Определение. Определителем третьего порядка называется число, вычисляемое по формуле:

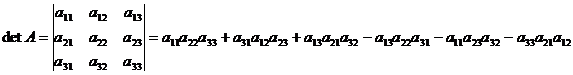(3)

Мнемонические правила для вычисления определителей 3-го порядка:

Правило треугольников

+ –

Правило Саррюса

– +

– – – + + +

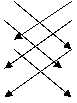
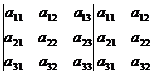
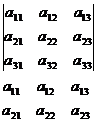Пример 2.Вычислить определитель третьего порядка .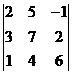

Решение.