Классическое и статистическое определение вероятности. Сочетания и размещения.
Формула Бернулли.
4.1.Вероятность всхожести семян пшеницы составляет 0,75. Найти вероятность того, что из 10 взятых наудачу семян взойдет: а) семь семян, б) не более трех семян, в) более 8 семян.
4.2.Вероятность рождения мальчика в семье равна 0,55. Наудачу выбрали 8 семей. Найти вероятность того, что: а) у пяти семей родился мальчик, б) мальчики родятся не менее чем у трех семей, в) у четырех семей родятся девочки.
4.3.Вероятность попасть в мишень при выстреле равна 0,8. Произведено 9 выстрелов. Найти вероятность того, что из этих выстрелов поразили мишень а) пять выстрелов, б) не более четырех, в) не менее шести.
4.4.Вероятность того, что в коробку положили бракованную деталь равна 0,2. В коробке лежат 12 деталей. Найти вероятность того, что в коробке находится: а) шесть бракованных деталей, б) не более трех, в) более десяти.
4.5.Мальчик подбросил монету 8 раз. Найти вероятность того, что герб выпал: а) 4 раза, б) не менее 5 раз, в) менее 3-х раз.
4.6. Вероятность выиграть партию игры у команды равна 0,6. Сыграно 9 партий. Найти вероятность того, что в сыгранных партиях команда выиграет: а) четыре игры, б) не более 5 игр, в) не менее 2-х игр.
4.7.Вероятность выигрыша по одному лотерейному билету равна 2/7. Покупатель приобрел 8 билетов. Найти вероятность того, что среди них а) три выигрышных, б) все невыигрышные, в) менее трех выигрышные.
4.8.Вероятность изготовить стандартную деталь равна 0,9. За час изготовили 15 деталей. Найти вероятность того, что среди этих деталей а) две нестандартные, б) более 3-x стандартные, в) не менее 12 стандартных деталей.
4.9.Вероятность того, что купленный телевизор потребует гарантийного ремонта равна 0,3. Найти вероятность того, что из десяти купленных телевизоров потребует ремонта: а) 4 телевизора, б) не один не потребует, в) потребует более 8 телевизоров.
4.10. В партии деталей 5% брака. Наудачу из этой партии выбрали 8 деталей. Какова вероятность того, что из выбранных деталей: а) 3 бракованных, б) все годные, в) менее двух бракованных.
4.11. Вероятность того, что при перевозке будет испорчено изделие, равна 0,2. После перевозки груза наудачу выбирают пять изделий. Найти вероятность того, что из этих изделий будет испорчено: а) два изделия, б) более трех изделий, в) менее двух изделий.
4.12. Вероятность вылечится от гриппа в течение недели, равна 0,75. В больницу обратились 7 пациентов. Найти вероятность того, что из них вылечится: а) 5 человек, б) менее пяти человек, б) более трех человек.
4.13. В отделе, состоящим из 9 человек, разыгрывают путевки в санаторий. Вероятность выиграть путевку равна 0,4. Найти вероятность того, что путевку выиграют: а) три человека, б) менее четырех человек, в) более семи человек.
4.14. Купили 12 саженцев яблок. Вероятность того, что саженец приживется равна 0,85. Найти вероятность того, что из этих саженцев приживется: а) 10 штук, б) более 9 штук, в) менее 3-х штук.
4.15. Студент знает 50 ответов на 60 вопросов. На собеседовании он вытягивает 5 вопросов. Найти вероятность того, что он знает: а) 4 вопроса, б) более трех вопросов, в) менее трех вопросов.
4.16. Вероятность того, что студент сдаст экзамен на «отлично» равна 0,25. Найти вероятность того, что из 8 отобранных студентов на «отлично» сдадут: а) 3 человека, б) менее 4-х человек, в) не менее шести человек.
4.17. В саду посадили 7 сортов роз. Вероятность того, что примется один из сортов роз равна 0,85. Найти вероятность того, что примется: а) 5 сортов, б) более трех сортов, в) менее четырех сортов.
4.18. Радист послал 10 сигналов, вероятность того, что сигнал будет принят 0,55. Найти вероятность того, что будет принято: а) семь сигналов, б) более шести сигналов, в) не более 3-х сигналов.
4.19. 70 % поступивших в университет оканчивают его через пять лет. Какова вероятность того, что из 30 первокурсников его окончат: а) 23 человека, б) более 25 человек, в) не более 15 человек.
4.20. При аварии должны сработать 4 сигнализатора. Вероятность того, что любой сигнализатор сработает, равна 0,85. Найти вероятность того, что при аварии сработает: а) три сигнализатора, б) более двух сигнализаторов, в) не менее трех сигнализаторов.
4.21. Рекламная компания отсылает по почте свои приглашения. Вероятность того, что на приглашение ответят 0,3. Найти вероятность того, что из 10 на приглашение ответят: а) 7 человек, б) менее 5 человек, в) более 8 человек.
4.22. В ящике находится 10 деталей завода «Импульс». Вероятность того, что деталь изготовленная заводом бракованная равна 0,1. Найти вероятность того, что среди этих деталей бракованных будет: а) три, б) менее 5, в) более восьми.
4.23. В коробке находятся цветные карточки. Вероятность вытянуть карточку зеленого цвета равна 0,3, а желтого 0,2. Из коробки вытянули восемь карточек. Найти вероятность того, что из них может быть: а) две зеленые и две красные, б) не более 3 красных, в) не менее шести зеленых.
4.24. В коробке находится шарики двух цветов: белые и синие. Вероятность вытянуть синий шар равна 0,4. Из коробки вынули 7 шариков. Найти вероятность того, что из них: а) более четырех белые, б) три синих, в) менее 5 синих.
4.25. Бабушка посадила рассаду помидоров 8 разных сортов. Вероятность того, что любой сорт примется равна 0,9. Найти вероятность того, что среди посаженных сортов принялось: а) 4 сорта, б) более пяти сортов, в) менее трех сортов.
4.26. Вероятность того, что через контрольный пункт проедет грузовая машина, равна 0,4. В течение часа через контрольный пункт проехало 10 машин. Найти вероятность того, что среди них было: а) пять грузовых, б) не менее семи грузовых, в) не более трех грузовых.
4.27. В розыгрыше призов участвуют 12 человек, при чем вероятность выиграть приз равна 0,25. Найти вероятность того, что из них приз выиграют: а) четыре человека, б) не более пяти человек, в) менее трех человек.
4.28. Мастер производит замер изделий. Вероятность того, что взятое изделие по размерам будет больше нормы равна 0,15. Мастер выбрал на проверку 10 изделий. Найти вероятность того, что среди них будет больше нормы: а) три изделия, б) более восьми, в) менее четырех.
4.29. В пионерском лагере детский врач взвешивает 10 детей из первой группы. Вероятность того, что вес ребенка соответствует нормативным показателям, равна 0,8. Найти вероятность того, что вес соответствует норме: а) у пяти детей, б) не менее чем у шести детей, б) более чем у восьми детей.
4.30. Вероятность того, что абитуриент поступить на нужный факультет, равна 0,65. Найти вероятность того, что из 15 абитуриентов, которые подали заявление на данный факультет, поступит: а) семь человек, б) более 12 человек, в) менее четырех человек.
4.31. Вероятность того, что ученик выполнит полностью домашнее задание, равна 0,7. Наудачу из класса выбирают 5 человек. Найти вероятность того, что из них домашнее задание выполнили: а) три человека, б) менее трех человек, б) более четырех человек.
4.32. Вероятность того, что спортсмен выполнил спортивный норматив, равна 0,8. Наудачу из команды отобрали 7 человек. Найти вероятность того, что норматив выполнили: а) 5 человек, б) более четырех человек, в) менее трех человек.
4.33. В магазин на продажу поступили 10 видов конфет. Вероятность того, что любой сорт будет продан полностью, равна 0,55. Найти вероятность того, что из всех конфет будет продано: а) 5 сортов, б) более семи сортов, в) не более трех сортов.
4.34. Вероятность всхожести семян огурцов равна 0,6. Найти вероятность того, что из 5 выбранных семян взойдет: а) четыре, б) более трех семян, в) менее трех семян.
4.35. Школьники написали контрольный диктант. Вероятность того, что ученик получит удовлетворительную оценку, равна 0,75. Наудачу отобрали 10 работ. Найти вероятность того, что из этих работ удовлетворительную оценку получат: а) семь работ, б) не более четырех работ, в) более восьми работ.
Индивидуальное домашнее задание №5
Равномерное распределение.
Найти вероятность попадания случайной величины X в интервал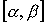 
, если она распределена равномерно в интервале 
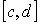. Вычислить плотность равномерного распределения и построить ее график.
|
Индивидуальное домашнее задание №14
Нормальное распределение.
Найти вероятность попадания случайной величины X в интервал 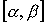, если она распределена по нормальному закону и имеет математическое ожидание m и дисперсию D. Вычислить плотность нормального распределения и построить ее график.
| Вариант | 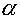 | 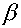 | m | D |
| 11,5 | ||||
| 7,5 | 0,16 | |||
| 0,09 | ||||
| 2,25 | ||||
| 6,25 | ||||
| 0,01 | ||||
| 0,09 | ||||
| 0,04 | ||||
| 11,5 | ||||
| 7,5 | 0,16 | |||
| 0,09 | ||||
| 2,25 | ||||
| 6,25 | ||||
| 0,01 | ||||
| 0,09 | ||||
| 2,25 | ||||
| 6,25 | ||||
| 0,01 | ||||
| 0,09 | ||||
| 0,04 | ||||
| 11,5 | ||||
| 0,16 | ||||
| 0,04 | ||||
| 3,5 | ||||
| 0,25 |
Индивидуальное домашнее задание №15
Классическое и статистическое определение вероятности. Сочетания и размещения.
1.1 В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
1.2 В цехе работают 10 мужчин и 6 женщин. По табельным номерам отобраны 8 человек. Найти вероятность того, что среди отобранных лиц окажутся 2 женщины.
1.3 Монета брошена 3 раза. Найти вероятность того, что хотя бы один раз появиться герб.
1.4 Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 7.
1.5 Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
1.6 В группе 12 студентов, среди них 4 отличника. По списку наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных студентов 2 отличника.
1.7 В коробке шесть одинаковых, занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера из влеченных кубиков появятся в возрастающем порядке.
1.8 Найти вероятность того, что при бросании трех игральных костей шестерка выпадет на одной кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой(и не равные шести).
1.9 Устройство состоит из 7 элементов, из которых 3 изношены. При включении устройства включаются случайным образом 5 элементов. Найти вероятность того, что включенными окажутся неизношенные элементы.
1.10 . Скольким способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти различных цветов.
1.11 Сколькими способами можно расставить белые фигуры (2 ладьи, 2 коня, 2 слона, ферзя и короля) на первой линии шахматной доски.
1.12 . В чемпионате России по футболу участвуют 16 команд. Сколькими способами тройка призеров.
1.13 . Сколько разных «слов» можно образовать при перестановке букв слова «математика».
1.14 Паспорт гражданина Российской Федерации состоит из серии и номера. Серия представляет собой 4 цифры, а номер – 6 цифр, расположенных в произвольном порядке. Определите возможное количество различных паспортов, которое может быть выдано гражданам Российской Федерации.
1.15 . В книжной лавке продавец студенту предлагает 8 различных книг по нужному предмету, цена на все книги одинакова. Однако студент располагает суммой денег, позволяющий купить только 4 книги. Сколько существует способов случайного выбора 4 книг из 8 предложенных.
1.16 . Кодовый замок открывается последовательным набором 5 различных цифр. Требуется определить число возможных кодов, которые можно подобрать для этого замка.
1.17 . Каждая буква слова «статистика» написана на разных карточках. Сколькими различными способами можно переставить эти буквы.
1.18 . Организация по продаже бытовой техники открывает трое новые торговые точки и выбирает помещения для аренды из 7 подходящих помещений. Сколько существует способов отбора, если выбор производится в случайном порядке.
1.19 .Шифр сейфа состоит из 6 цифр, которые должны набираться последовательно и могут повторяться. Чему в этом случае равно общее число всех возможных комбинаций шифра.
1.20 . На карточках разрезной азбуки написаны 33 буквы алфавита. 5 карточек вынимают наугад и укладывают на стол в порядке появления. Сколько существует способов составить разные слова из 5 букв. Сколько способов будут содержать буквы А, Б, и В.
1.21 . Три работника строительной организации были награждены за хорошую работу туристической путевкой. Руководству организации представляют свои услуги 5 различных туристических фирм по организации туристических поездок. Решено, что любая фирма может получить только один заказ на туристическую путевку. Сколько имеется способов получения путевок при случайном выборе фирм, если учитывать, что получение одним и тем же работником путевки от различных фирм неоднозначно.
1.22 . Три работника строительной организации были награждены за хорошую работу туристической путевкой. Руководству организации представляют свои услуги 5 различных туристических фирм по организации туристических поездок. Решено, что любая фирма может получить только один заказ на туристическую путевку. В скольких случаях при случайном выборе воспользуются услугами первой фирмы.
1.23 . Числа 10,11,12….20 расставляют в один ряд. Сколько существуют способов расстановки этих чисел таким образом, чтобы все четные числа стояли подряд.
1.24 . Водительское удостоверение имеет номер, состоящий из трех букв и трех цифр. Чему равно общее число возможных номеров водительских удостоверений, считая, что число букв русского алфавита, используемых для составления шифра, -26, буквы занимают три первые позиции шифра и не повторяются, а цифры могут повторяться.
1.25 . В классе 12 девочек и 10 мальчиков. Классный руководитель выбирает 5 человек, которые пойдут на концерт. Какова вероятность того, что это будет 2 девочки и 3 мальчика.
1.26 . Из 30 вопросов по собеседованию студент знает 25 вопросов. Какова вероятность того, что взятый наудачу студентом билет, содержащий 3 вопроса, будет состоять из подготовленных им вопросов.
1.27 . В ящике для мячей находятся 7 мячей красного цвета, 5 мячей зеленого цвета, 4 мяча синего цвета. Воспитатель наугад отбирает 5 мячей. Какова вероятность того, что это будет 2 мяча красного цвета, 2 мяча зеленого цвета и один мяч синего цвета.
1.28 . Бабушка вяжет свитер, состоящий из полос четырех разных цветов. У бабушки есть нитки 9 разных цветов. Сколькими способами можно составить цветовую гамму свитера.
1.29 . Брошены три игральные кости. Какова вероятность того, что сумма очков на гранях будет равна восьми.
1.30 . В ящике находятся 15 деталей 1 сорта, 20 деталей второго сорта и 10 деталей третьего сорта. Наудачу извлекают две детали. Какова вероятность того, что: а) одна деталь первого сорта, вторая третьего сорта, б) две детали второго сорта
1.31 . В коробке находится 5 красных и 3 синих карандаша. Какова вероятность того, что три карандаша взятые наудачу будут одного цвета.
1.32 . Сколько различных четырехзначных чисел можно записать при помощи цифр 1, 2, 3. Найти вероятность того, что записано число 1231.
1.33 . Букет составляют из цветов разного сорта. Всего имеется 9 разных сортов. В букет должно войти 5 различных сортов цветов. Сколькими способами можно букет.
1.34 . На полке стоят 25 книг, из которых 17 в переплете. Ученик берет наугад 4 книги. Какова вероятность того, что две из них в переплете.
1.35 . В кармане находится 4 монет достоинством 5 рублей и 8 монет достоинством 2 рубля. Наудачу вынимают несколько монет. Какова вероятность того, что сумма будет составлять 14 рублей.