Глава 9. основы алгоритмизации

Понятие алгоритма

В основу работы ЭВМ положен программный принцип управления, состоящий в том, что ЭВМ выполняет действия по заранее заданной программе. Программа – это упорядоченная последовательность команд, которые понимает ЭВМ.

В основе любой программы лежит алгоритм. Алгоритм – это полное и точное описание на некотором языке конечной последовательности правил, указывающих исполнителю действия, которые он должен выполнить, чтобы за конечное время перейти от (варьируемых) исходных данных к искомому результату.

Термин «алгоритм» произошел от имени арабского математика аль-Хорезми (IX в.), которым были описаны общие правила (названные позднее алгоритмами) выполнения основных арифметических действий в десятичной системе счисления. Эти алгоритмы изучаются в начальных разделах школьной математики. К числу алгоритмов школьного курса математики относятся также правила решения определенных видов уравнений или неравенств, правила построения различных геометрических фигур и т. п. Понятие алгоритма используется не только в математике, но и во многих областях человеческой деятельности, например, говорят об алгоритме управления производственным процессом, алгоритме управления полетом ракеты, алгоритме пользования бытовым прибором. Причем интуитивно под алгоритмом понимают некоторую систему правил, обладающих определенными свойствами.

Далее, изучая понятие алгоритма, мы будем предполагать, что его исполнителем является автоматическое устройство - ЭВМ. Это накладывает на запись алгоритма целый ряд обязательных требований. Сформулируем эти требования в виде перечня свойств, которыми должен обладать алгоритм, адресуемый к исполнению на ЭВМ.

1. Первым свойством алгоритма является дискретный (пошаговый) характер определяемого им процесса. Возникающая в результате такого разбиения запись алгоритма представляет собой упорядоченную последовательность отдельных предписаний (директив, команд), образующих прерывную/дискретную структуру алгоритма: только выполнив требования одного предписания можно приступить к исполнению следующего.

2. Исполнитель может выполнить алгоритм, если он ему понятен, то есть записан на понятном ему языке и содержит предписания, которые исполнитель может выполнить. Набор действий, которые могут быть выполнены исполнителем, называется системой команд исполнителя. Алгоритм не должен содержать описания действий, не входящих в систему команд исполнителя, т. е. своей структурой команд и формой записи алгоритм должен быть ориентирован на конкретного исполнителя.

3. Алгоритмы, предназначенные для исполнения техническим устройством, не должны содержать предписаний, приводящих к неоднозначным действиям. Алгоритм рассчитан на чисто механическое исполнение, и если применять его повторно к одним и тем же исходным данным, то всегда должен получаться один и тот же результат; при этом и промежуточные результаты, полученные после соответствующих шагов алгоритмического процесса, тоже должны быть одинаковыми. Это свойство определенности и однозначности – детерминированности - алгоритма позволяет использовать в качестве исполнителя специальные машины-автоматы.

4. Основополагающим свойством алгоритма является его массовость, применимость к некоторому классу объектов, возможность получения результата при различных исходных данных на некоторой области допустимых значений. Например, исходными данными в алгоритмах аль-Хорезми могут быть любые пары десятичных чисел. Конечно, его способ не всегда самый рациональный по сравнению с известными приемами быстрого счета. Но смысл массовости алгоритма состоит как раз в том, что он одинаково пригоден для всех случаев, требует лишь механического выполнения цепочки простых действий и при этом исполнителю нет нужды в затратах творческой энергии.

5. Цель выполнения алгоритма – получение конечного результата посредством выполнения указанных преобразований над исходными данными. В алгоритмах аль-Хорезми исходными данными являются два десятичных числа, результатом – также некоторое десятичное число. Причем при точном исполнении всех предписаний алгоритмический процесс должен заканчиваться за конечное число шагов. Это обязательное требование к алгоритмам – требование их результативности или конечности.

В математике известны вычислительные процедуры алгоритмического характера, не обладающие свойством конечности. Например, процедура вычисления числа p. Однако, если мы введем условие завершения вида «закончить после получения n десятичных знаков числа p», то получим алгоритм вычисления n десятичных знаков числа p. На этом принципе построены многие вычислительные алгоритмы.

6. Если алгоритм должен быть выполнен не просто за конечное время, а за разумное конечное время, то речь идет об эффективности алгоритма. Время выполнения алгоритма очень важный параметр, однако, понятие эффективности алгоритма трактуется шире, включая такие аспекты, как сложность, необходимые ресурсы, информационно-программное обеспечение. Эффективность алгоритма часто определяет возможность его практической реализации.

Алгоритмическая система

Понятие «алгоритмическая система» дает формальный ответ на вопрос, что должно быть известно и доступно разработчикам алгоритмов. Алгоритмическаясистема – набор средств и понятий, позволяющих строить некоторое множество алгоритмов для решения определенного класса задач. Алгоритмическая система определяется наличием четырех составляющих ее частей:

1) множеством входных объектов или исходных данных, подлежащих обработке алгоритмами данной системы;

2) множеством выходных объектов или результатов выполнения алгоритмов данной системы;

3) системой команд исполнителя, то есть набором тех действий, которые может выполнять исполнитель, и которые мы можем описывать в алгоритмах, что собственно является ориентацией алгоритмической системы на конкретного исполнителя;

4) языком описания алгоритмов – языком исполнителя; язык, на котором описан алгоритм, должен быть понятен исполнителю и не должен включать в свой состав указания на невозможные для исполнителя действия, а также обращения к входным или выходным объектам, не принадлежащих к множеству входных или выходных объектов данной алгоритмической системы.

В качестве примера рассмотрим алгоритмическую систему, предназначенную для построения алгоритмов обработки данных – алгоритмов обработки символьных последовательностей (строк) из ограниченного алфавита символов. Входными объектами такой системы являются строки символов конечной длины. С помощью специальных приемов можно преобразовать в строки символов практически любую информацию, в том числе формулы, таблицы, рисунки. Результат обработки данных также представляет собой строки символов. Алгоритмические системы для обработки данных строятся на одном и том же множестве входных и выходных объектов.

Исполнителем в современных системах обработки данных является вычислительная машина. Набор операций, выполняемых ЭВМ, весьма ограничен, однако, комбинируя их в нужной последовательности, можно строить весьма сложные алгоритмы решения множества самых различных задач. Язык, на котором записываются алгоритмы, адресованные вычислительной машине, опирается на систему команд данной ЭВМ. Алгоритм, написанный на машинном языке, представляет собой закодированную специальным образом последовательность команд, адресованных различным устройствам ЭВМ.

Отметим принципиальную особенность алгоритмических систем обработки данных. В таких системах текст алгоритма также является последовательностью символов, которую можно преобразовать в той же алгоритмической системе. Следовательно, открывается возможность составлять алгоритмы преобразования алгоритмов, обрабатывая при этом тексты, реализующие преобразуемые алгоритмы. Это и создает ту удивительную логическую гибкость, которая превратила ЭВМ в принципиально новый инструмент обработки данных, обладающий колоссальными возможностями. Одним из примеров преобразования алгоритма с помощью ЭВМ из одной формы в другую является его «трансляция» – перевод с некоторого алгоритмического языка на язык машины.

Алгоритмизация

Алгоритмизация – процесс разработки и описания алгоритма решения какой-либо задачи.

Пусть мы имеем некоторую математическую задачу, которая может быть решена одним из известных математических методов. Как приступить к процессу построения алгоритма решения такой задачи?

Поскольку речь идет о разработке алгоритма для ЭВМ, то нужно сначала проанализировать возможность его машинной реализации, оценить ресурсы и возможности конкретной ЭВМ, имеющейся в распоряжении (в том числе, допустимую точность вычислений, объем запоминающих устройств, быстродействие, информационно-программное обеспечение).

Непосредственная разработка алгоритма начинается с осознания существа поставленной задачи, с анализа того, что нам известно, что следует получить в качестве результата, в какой форме нужно представить исходные данные и результаты вычислений. Следующая ступень – разработка общей идеи алгоритмического процесса и анализа этой идеи. После этого можно приступить к более детальной разработке уже задуманного конкретного алгоритма. И вот этот процесс разработки конкретного алгоритма, в соответствии с определением самого понятия «алгоритм», заключается в последовательном выполнении следующих пунктов:

1) разложении всего вычислительного процесса на отдельные шаги – возможные составные части алгоритма, что определяется внутренней логикой самого процесса и системой команд исполнителя;

2) установлении взаимосвязей между отдельными шагами алгоритма и порядка их следования, приводящего от известных исходных данных к искомому результату;

3) полном и точном описании содержания каждого шага алгоритма на языке выбранной алгоритмической системы;

4) проверке составленного алгоритма на предмет, действительно ли он реализует выбранный метод и приводит к искомому результату.

В результате проверки могут быть обнаружены ошибки и неточности, что вызывает необходимость доработки и коррекции алгоритма – возвращение к одному из предыдущих пунктов. Во многих случаях разработка алгоритма включает в себя многократно повторяющуюся процедуру его анализа и коррекции.

Процедура анализа и коррекции алгоритма производится не только с целью устранения ошибок, но и с целью улучшения, то есть оптимизации алгоритма. При определенном методе решения задачи оптимизация проводится с целью сокращения алгоритмических действий и упрощения по возможности самих этих действий. При этом алгоритм должен оставаться «эквивалентным» исходному. Будем называть два алгоритма эквивалентнымиесли выполняются следующие условия:

1) множество допустимых исходных данных одного из них является множеством допустимых исходных данных и другого; из применимости одного алгоритма к каким-либо исходным данным следует применимость и другого алгоритма к этим данным;

2) применение этих алгоритмов к одним и тем же исходным данным дает одинаковые результаты.

Приведем пример двух эквивалентных алгоритмов. Пусть нам надо подсчитать общую сумму чисел, приведенных в табл. 9.1.

Таблица 9.1. Целые числа

Эквивалентными будут алгоритмы подсчета общей суммы «по строкам»: 5 + 1 + 3 + 8 + 10 + 9 + 6 + 1 + 5 + 10 + 1 + 1 = 60 - и «по столбцам»: 5 + 10 + 5 + 1 + 9 + 10 + 3 + 6 + 1 + 8 + 1 + 1 = 60. Заметим, что для данной таблицы считать проще по столбцам.

Средства записи алгоритмов

Характер языка, используемого для записи алгоритмов, определяется тем, для какого исполнителя предназначен алгоритм. Возможности исполнителя алгоритмов определяют уровень используемых языковых средств, то есть степень детализации и формализации предписаний в алгоритмической записи. Если алгоритм предназначен для исполнителя-человека, то его запись может быть не полностью формализована и детализирована, но должна оставаться понятной и корректной. Для записи таких алгоритмов может использоваться естественный язык. Для записи алгоритмов, предназначенных для исполнителей-автоматов, необходимы строгая формализация средств записи и определенная детализация алгоритмических предписаний. В таких случаях применяют специальные формализованные языки.

Поскольку одним из пользователей языка описания алгоритмов, так или иначе, остается человек, то, говоря об уровне языка, имеют в виду также и уровень его доступности для человека.

К настоящему времени в информатике сложились вполне определенные традиции в представлении алгоритмов.

Словесная запись алгоритмов

Самой распространенной формой представления алгоритмов, адресуемых человеку, является обычная словеснаязапись. В этой форме могут быть выражены любые алгоритмы. Но если такой алгоритм предназначен для его дальнейшей реализации на вычислительном устройстве, то принято придерживаться более формализованного способа построения фраз с тщательно отобранным набором слов. Кроме того, необходимо указывать начало и конец алгоритма, отмечать момент ввода в вычислительное устройство значений исходных данных и вывода/печати полученного результата. В вычислительных алгоритмах широко используется общепринятая математическая символика, язык формул. Вводится необходимая в вычислительной практике операция присваивания:

у := А

(читается: «у присвоить значение А»), где у – переменная; А – некоторое выражение/формула. Следует сначала выполнить все действия, предусмотренные формулой А, а затем полученный результат сохранить в качестве значения переменной у. Выражение А в частном случае может быть переменной или числом. Например,

x := sin a – присвоить переменной х значение синуса;

y := x – присвоить переменной у значение переменной x;

z := 5.7 – считать значением переменной z число 5,7;

k := k + 1 – значение переменной k увеличить на единицу.

Введенные соглашения позволяют представлять словесные алгоритмы в достаточно компактной и наглядной форме.

Пример 9.1. Составим алгоритм вычисления коэффициентов приведенного квадратного уравнения x² + px + q = 0, корни которого x₁, x₂ известны. Коэффициенты такого уравнения определяются по формулам:

p = –(x₁+x₂),

q = x₁x₂.

Предположим, что правила выполнения арифметических операций сложения, вычитания и умножения известны исполнителю. Тогда искомым алгоритмом будет следующая система предписаний:

Начало.

1. Ввести x₁, x₂.

2. p = –(x₁+x₂).

3. q = x₁x₂.

4. Вывести p, q.

Конец. □

В приведенной записи алгоритма ни в одном из предписаний нет указания на то, к какому следующему предписанию надо перейти. Предполагается, что в случае отсутствия специальных указаний предписания алгоритма выполняются в порядке их следования. Такое выполнение предписаний в алгоритме называется естественным ходом выполнения алгоритма, а сам алгоритм называется линейным.

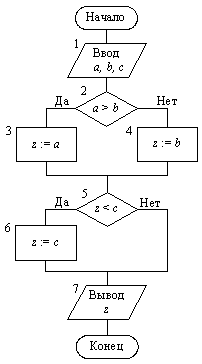
Пример 9.2. Составим алгоритм определения максимального числа из трех чисел: z = max (a, b, c).

Решение задачи на ЭВМ можно получить, действуя следующим образом. Сначала найдем наибольшее из двух чисел, например, сравнив между собой a и b. Предположим, что исполнитель может выполнить операцию сравнения «больше». Найденное наибольшее число "запомним" в качестве значения переменной z. Далее сравним значение переменной z с оставшимся числом c. Если с больше z, то присвоим z новое значение – значение с, в противном случае, значение z останется прежним. В результате переменная z будет равна наибольшему из a, b, c и будет являться искомым результатом.

Изложенные рассуждения можно представить в виде следующей словесной записи алгоритма:

Начало.

1. Ввести a, b, c.

2. Если a > b, то z := a,

иначе z := b.

3. Если c > z, то z := c.

4. Вывести z

Конец.

Ход выполнения алгоритма зависит от результатов проверки условий а > b и c > z. Если для введенных значений a, b действительно a > b, то выполняется операция z := a; если нет, то выполняется z := b. Таким образом, в зависимости от результата проверки условия a > b требуется выполнить различные действия. В алгоритме на этом шаге предусмотрены оба возможных направления дальнейших вычислений. При проверке условия c > z операция z := c может выполняться, если действительно c > z, или не выполняться, в противном случае. □

Вычислительный процесс, который в зависимости от выполнения некоторых условий реализуется по одному из нескольких возможных, заранее предусмотренных направлений, называется разветвляющимся. Каждое отдельное направление называется ветвью вычислений. Выбор той или иной ветви осуществляется при выполнении алгоритма в результате проверки этих условий и определяется свойствами исходных данных и промежуточных результатов. При разработке алгоритма должны быть учтены все возможные ветви вычислений.

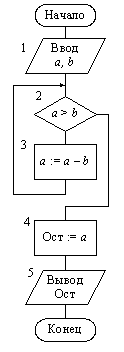
Пример 9.3. Составим алгоритм определения остатка от деления двух целых неотрицательных чисел А и В, где В ¹ 0. Рассматривая деление как многократное вычитание делителя В из делимого А, получим алгоритм, состоящий из следующих шагов:

Начало.

1. Ввести A, B.

2. Если A < B, то перейти к шагу 5,

иначе перейти к шагу 3.

3. A := A – B.

4. Перейти к шагу 2.

5. ОСТ := A.

6. Вывести ОСТ.

Конец.

Шаги 2, 3, 4 записаны в алгоритме один раз, а могут выполняться многократно. Многократно повторяемые участки вычислений образуют так называемый цикл. Вычислительный процесс, содержащий многократные вычисления по одним и тем же математическим зависимостям, но для различных значений входящих в них переменных, называется циклическим. Переменные, изменяющиеся в цикле, называются переменными цикла, а действия, повторяемые в цикле, – телом цикла. Количество повторений цикла определяется значениями переменных, входящих в условие его окончания.

Чтобы лучше понять характер циклических процессов, рассмотрим подробнее структуру приведенного алгоритма. Первый шаг алгоритма представляет собой подготовку цикла: задание начальных значений переменным цикла перед первым его выполнением. Тело цикла – действия, многократно повторяемые в цикле (шаги 2, 3, 4). В каждом конкретном случае число повторений этих действий будет различным. Шаг 3 обеспечивает модификацию (изменение) значений переменной цикла А, входящей в условие его окончания. Управление циклом осуществляется на шаге 2. Проверяется условие окончание цикла (А < В), и осуществляется, либо выход из цикла, либо возврат на его повторение. Очень важно правильно сформулировать условие окончания цикла.

Поняв сущность и структуру циклических алгоритмов, можно записать алгоритм более компактно:

Начало.

1. Ввести A, B.

2. Пока A ³ B, выполнять A := A – B.

3. ОСТ := A.

4. Вывести ОСТ.

Конец.

Предписание «Пока А ³ В выполнять А := А - В» надо понимать следующим образом: если А больше или равно В, то выполнить операцию А := A - В и перейти опять на проверку условия А ³ В; если А меньше В, то перейти к выполнению следующего предписания (шаг 3), не выполняя операцию А := A - В. □

Схемы алгоритмов

Схема алгоритма – это графический способ его представления с элементами словесной записи. Каждое предписание алгоритма изображается с помощью плоской геометрической фигуры – блока. Отсюда название: блок-схема. Переходы от предписания к предписанию изображаются линиями связи – линиями потоков информации, а направление переходов – стрелками. Различным по типу выполняемых действий блокам соответствуют различные геометрические фигуры. Приняты определенные стандарты графических изображений блоков (табл. 9.2).

Таблица 9.2. Изображение блоков в схемах алгоритмов

Наименование символа	Обозначение и размеры	Функция
Процесс (вычислительный блок)		Выполнение операции или группы операций, в результате которых изменяются значение, форма представления или расположение данных
Решение (логический блок)		Выбор направления выполнения алгоритма в зависимости от некоторых условий
Модификация (заголовок цикла)		Выполнение операций по управлению циклом – повторением команды или группы команд алгоритма
Пуск-останов (начало-конец)		Начало или конец выполнения программы или подпрограммы
Предопределенный процесс (вызов подпрограммы)		Вызов и использование ранее созданных и отдельно описанных алгоритмов (подпрограмм)
Ввод-вывод		Общее обозначение ввода или вывода данных в алгоритме безотносительно к внешнему устройству
Соединитель		Указание прерванной связи между блокам в пределах одной страницы
Межстраничный соединитель		Указание прерванной связи между блоками, расположенными на разных листах

Рассмотрим общие правила построения схем алгоритмов.

1. Для конкретизации содержания блока и уточнения выполняемого действия внутри блока помещаются краткие пояснения – словесные записи с элементами общепринятой математической символики (рис. 9.1, а).

2. Основное направление потока информации в схемах может не отмечаться стрелками. Основное направление – сверху вниз и слева направо. Если очередность выполнения блоков не соответствует этому направлению, то возможно применение стрелок (рис. 9.1, б).

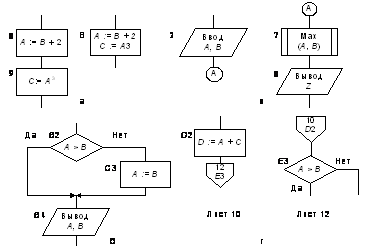
Рис. 9.1. Примеры изображения элементов схем алгоритмов

3. По отношению к блоку линии могут быть входящими и выходящими. Количество входящих линий принципиально не ограничено. Количество выходящих линий регламентировано и зависит от типа блока. Например, логический блок должен иметь не менее двух выходящих линий, каждая из которых соответствует одному из возможных направлений вычислений. Блок модификации должен иметь две выходящие линии, одна соответствует повторению цикла, вторая – его окончанию.

4. Допускается разрывать линии потока информации, размещая на обоих концах разрыва специальный символ «соединитель» (рис. 9.1, в, г). В пределах одной страницы используется символ обычного соединителя, во внутреннем поле которого помещается маркировка разрыва либо отдельной буквой, либо буквенно-цифровой координатой блока, к которому подходит линия потока. Если схема располагается на нескольких листах, переход линий потока с одного листа на другой обозначается с помощью символа «межстраничный соединитель». При этом на листе с блоком-источником соединитель содержит номер листа и координаты блока-приемника, а на листе с блоком-приемником – номер листа и координаты блока-источника.

5. Нумерация блоков осуществляется либо в левом верхнем углу блока в разрыве его контура, либо рядом слева от блока (рис. 9.1, а). Принцип нумерации может быть различным, наиболее простой – сквозная нумерация. Блоки начала и конца не нумеруются.

6. Для блоков приняты следующие размеры: а = 10, 15, 20 мм; b = 1,5а. Если необходимо увеличить размер блока, то допускается увеличение на число, кратное пяти. Необходимо выдерживать минимальное расстояние 3 мм между параллельными линиями потоков и 5 мм между остальными символами.

С помощью блок-схем можно изображать самые различные алгоритмы, например, линейной (рис. 9.2), разветвляющейся (рис. 9.3) и циклической структур (рис. 9.4).

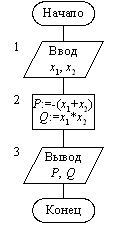
Рис. 9.2. Алгоритм вычисления коэффициентов
приведенного квадратного уравнения

Пример 9.4. Рассмотрим задачу определения наибольшего общего делителя (НОД) двух целых положительных чисел M, N.

В математике известен алгоритм решения этой задачи – алгоритм Евклида, который заключается в последовательном делении вначале большего числа на меньшее, затем меньшего на полученный остаток, первого остатка на второй остаток и т.д. до тех пор, пока в остатке не получится нуль. Последний по счету делитель и будет искомым результатом.

Рис. 9.3. Алгоритм выбора максимального числа из трех заданных чисел	Рис. 9.4. Алгоритм определения остатка от деления двух целых неотрицательных чисел

Сформулируем алгоритм Евклида несколько иначе, рассматривая деление как многократное вычитание:

1. Если числа равны между собой, то взять в качествеНОД любое из них.

2. Если числа не равны между собой, то большее из чисел заменить их разностью и вернуться к шагу 1.

Алгоритм Евклида может быть представлен следующей словесной записью:

Начало.

1. Ввести М, N.

2. Пока М¹N выполнять:

Если M > N, то M := M-N;

иначе N := N-M.

3. НОД := М.

4. Вывести НОД.

Конец.

Блок-схема алгоритма Евклида представлена на рис. 9.5, где блок 1 есть подготовка цикла, блок 2 – управление циклом, блоки 3, 4, 5 – тело цикла (разветвляющаяся структура), из них блоки 4, 5 являются блоками модификации значений переменных цикла M и N. □

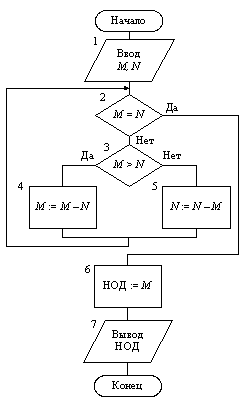
Рис. 9.5. Алгоритм Евклида

Блок-схемы являются исключительно простым и наглядным способом представления алгоритмов. Их очень полезно использовать при разработке общей структуры алгоритма, чтобы отчетливо представить себе алгоритм в целом и проследить все логические связи между его отдельными частями, проверить все ли возможные варианты решения поставленной задачи нашли в нем отражение.

Блок-схемы не накладывают никаких ограничений на степень детализации в изображении алгоритма. Это определяется программистом. Однако следует помнить, что схемы общего характера малоинформативны, а излишне подробные схемы проигрывают в наглядности. При разработке сложных алгоритмов, чтобы уяснить сущность выполняемых действий и выявить основные связи, сначала пытаются представить его общей схемой в виде достаточно крупных блоков. Затем эти крупные блоки разбивают на более мелкие, составляя более детальные схемы и проверяя их логическую правильность. Именно так мы поступили при разработке алгоритма Евклида, при этом использовали и словесную форму записи, и блок-схему.

Замечание. Стандарты предусматривают использование циклической структуры общего вида (безотносительно к типу цикла), представленной справа. Условие продолжения или окончания цикла может быть указано как в верхнем, так и в нижнем блоке. Её применение целесообразно только в простых алгоритмах, в более сложных, она теряется в общей структуре алгоритма ввиду отсутствия явной передачи управления.

Структурограммы

В практике структурного программирования для представления алгоритмов используются также структурограммы (схемы Насси-Шнейдермана). Этот способ позволяет изображать схему передач управления в алгоритме не с помощью явного указания линий потоков информации, а с помощью представления вложенности структур – функциональных блоков, которые используются для описания выполняемых действий. Некоторые из используемых в этом способе блоков соответствуют их изображению в схемах алгоритмов. Для изображения алгоритмов в структурограммах используются следующие блоки.

1. Блок обработки (вычислений). Каждый блок является блоком обработки. Каждый прямоугольник внутри любого блока представляет собой также блок обработки.
2. Блок следования. Этот блок объединяет ряд следующих друг за другом процессов обработки.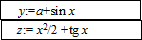
3. Блок решения. Этот блок применяется для обозначения структуры ветвления. Условие располагается в верхнем треугольнике, варианты решения – по сторонам треугольника, процессы обработки – в нижних прямоугольниках. Если блок решения является сокращенным (отсутствует одна из ветвей), то структурограмма видоизменяется соответствующим образом.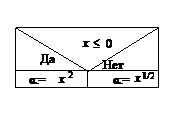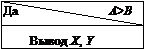
4. Блок варианта реализует структуру многоальтернативного выбора. Варианты, которые можно сформулировать точно, размещаются слева, остальные объединяются в один, называемый выходом по несоблюдению условий, располагаемый справа. Правую часть можно оставить незаполненной или опустить.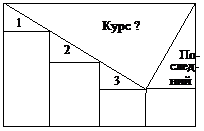
5. Блок цикла с предусловием реализует циклическую структуру с проверкой условия в начале цикла. Условие продолжения цикла размещается в верхней полосе, сливающейся с левой, указывающей границу цикла. Данный блок может быть использован и для обозначения цикла с параметром, тогда вверху указывают закон изменения параметра цикла.
6. Блок цикла с постусловие аналогичен блоку цикла с предусловием, но условие окончания цикла располагают внизу. Каждый блок имеет форму прямоугольника и может быть вписан в любой внутренний прямоугольник любого другого блока. Блоки дополняются элементами словесной записи с использованием математической символики. На рис. 9.6 приведен пример структурограммы алгоритма Евклида.
	Рис. 9.6. Структурограмма алгоритма Евклида