Логические элементы и логические схемы
Основным логическим операциям, используемым в ЭВМ, соответствуют следующие логические элементы, каждый из которых имеет два входа (слева) и один выход (справа).
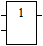 | 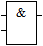 | 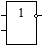 | 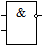 |
| дизъюнкция | конъюнкция | стрелка Пирса | штрих Шеффера |
Для отрицания отдельный элемент применяется редко, так как отрицание (обозначается кружком) может быть помещено как на входы
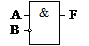 | F = A 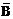 |
так и на выходы логических элементов
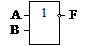 | F = 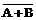 . . |
Логические элементы реализуются аппаратно с помощью транзисторов, резисторов и т. п. Значению «истина» соответствует наличие напряжения на входах и на выходах, значению «ложь» – его отсутствие.
Логические элементы соединяются между собой и подсоединяются к входам, соответствующим переменным X, Y, Z, и образуют логическую схему. Как правило, логическая схема имеет один выход.
Пример 6.7. Построить логическую схему, реализующую упрощенную функцию из примера 6.1.
Решение. Каждый логический элемент имеет только два входа, поэтому перегруппируем слагаемые:
f(X, Y, Z) = X + Y  +
+  Z = (X + Y
Z = (X + Y  ) +
) +  Z.
Z.
Запишем схему, соответствующую логической функции (рис. 6.1). Черные точки на соединителях элементов обозначают разветвление, чтобы отличать его от наложения соединителей. □
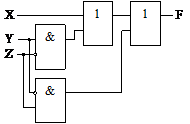
Рис. 6.1. Логическая схема, соответствующая
функции f(X, Y, Z) = X + Y  +
+  Z
Z
Перед построением логической схемы функцию минимизируют, чтобы получить схему с минимальным количеством элементов.
Пример 6.8. Построить функцию, соответствующую схеме
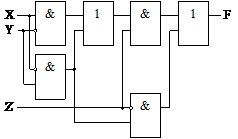
Минимизировать функцию и по ней построить логическую схему.
Решение. Выпишем функцию, соответствующую схеме:
f(X, Y, Z) = (X  +
+ 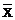 Y)Z +
Y)Z + 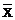 Y
Y  .
.
Минимизируем функцию по методу Блейка, для этого приведем ее к виду суммы произведений – раскроем скобки:
f(X, Y, Z) = (X  +
+ 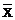 Y)Z +
Y)Z + 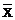 Y
Y  = X
= X  Z +
Z + 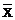 YZ +
YZ + 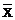 Y
Y  .
.
Перейдем ко второму этапу минимизации – применим операцию склеивания:
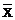 YZ +
YZ + 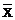 Y
Y  =
= 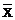 YZ +
YZ + 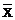 Y
Y  +
+ 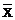 Y.
Y.
В результате второго этапа получим
f(X, Y, Z) = X  Z +
Z + 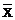 YZ +
YZ + 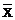 Y
Y  +
+ 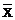 Y.
Y.
Перейдем к третьему этапу – применим операцию поглощения:
f(X, Y, Z) = X  Z +
Z + 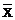 Y.
Y.
Функция минимизирована. Построим по ней логическую схему (рис. 6.2).
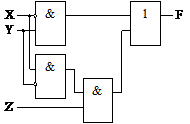
Рис. 6.2. Логическая схема, соответствующая
функции f(X, Y, Z) = X  Z +
Z + 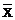 Y
Y
В результате получена логическая схема, число элементов которой меньше, чем у исходной. □
Количество входов логического элемента называется коэффициентом объединения (Коб). У всех рассмотренных элементов коэффициент объединения Коб = 2, но существуют элементы с коэффициентом объединения Коб = 3; 4; 8. Как правило, логические элементы не выпускаются отдельно, а интегрированы в некоторую логическую схему.
Для удешевления производства вместо логических элементов двух типов И и ИЛИ используют элементы одного типа И-НЕ или ИЛИ-НЕ. Чаще используют элементы И-НЕ.
Пример 6.9. Построить логическую схему по функции в базисе NAND из примера 6.5.
Решение. Функция в базисе NAND имеет вид:
f(X, Y, Z) = (Y ½ Z) ½ (Y ½ X).
Логическая схема представлена на рис. 6.3. □
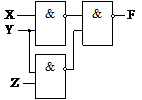
Рис. 6.3. Логическая схема, соответствующая
функции f(X, Y, Z) = (Y ½ Z) ½ (Y ½ X)
