Коэффициент гидравлического сопротивления при турбулентном течении. Графики Никурадзе и Мурина.

Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид: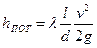

Различие заключается лишь в значениях коэффициента гидравлического трения λ. Этот коэффициент зависит от числа РейнольдсаRe и от безразмерного геометрического фактора - относительной шероховатости Δ/d (или Δ/r₀, где r₀ - радиус трубы).

Первые систематические опыты для выявления влияния различ­ных параметров на величину λ были проведены Никурадзе под руко­водством Прандтля в 20-х годах XX века в Германии.

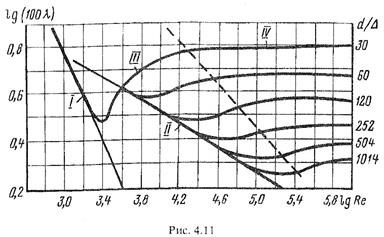
Эти опыты проводились в латунных трубах, глад­ких, что достигалось шлифовкой и с искусственной однородной ше­роховатостью, которая создавалась наклеиванием зерен песка определенного размера на внутреннюю поверхность труб. В трубах с полученной таким образом определенной шероховатостью при раз­ных расходах измерялась потеря напора и вычислялся коэффициент λ, значения которого наносились на график в функции числа Рейнольдса. Результаты опытов Никурадзе представлены графически на рис. 4.11 На этом графике по горизонтальной оси отложены величи­ны lgRe, а по вертикальной оси — lg(l00 λ). Кривые построены по данным опытов с трубами относительной шероховатости от ε=∆/d= 0,001 (самая нижняя кривая) до ε=0,033 (самая верхняя кривая).

Анализируя представленный график, можно сделать следу­ющие выводы:

Существуют четыре различные области.

Область ламинарного режима (I). В области ламинарного режи­ма (т.е. при Re< 2300, чему соответствует lgRe< 3,36) опытные точ­ки, независимо от шероховатости стенок, уложились на одну прямую линию I. Следовательно, здесь λ зависит только от числа Рейнольдса и не зависит от шероховатости, т.е. λ=f (Re).

Остальные участки кривых (II, III, IV) относятся к турбулентно­му движению.

В области перехода от ламинарного движения к турбулентному Re = 2000-4000 (3,3<lgRe< 3,6) наблюдается большой разброс опытных точек и кривая между I и II па рис. 4.11 проведена условно.

Область гидравлически гладких труб (II). В этой области опыт­ные точки для труб с различной шероховатостью располагаются в не­котором диапазоне чисел Re на одной прямой II, отрываясь от нее в сторону возрастания коэффициента λ тем раньше, чем больше шероховатость стенок. Таким образом, при некоторых условиях шерохо­ватость не оказывает влияния на потери напора также и при турбулентном движении, т.е. и здесь λ =f(Re). Область смешанного трения (III). Здесь каждая кривая относится к определенному значению относительной шероховатости и величина также меняется с изменением числа Рейнольдса, т.е. коэф­фициент гидравлического сопротивления зависит как от числа Re, так и от ε(λ =f(Re,ε))

Область «вполне шероховатых труб» (IV), При увеличении числа Re кривые области IIIпереходят в линии, параллельные оси lgRe, т,е.коэффициентλв этой области не зависит от числа Re и оп­ределяется только относительной шероховатостью. Полуэмпиричекая теория турбулентности позволяет предложить выражение для коэффициента λ, исходя из распределения скорости в живых сечени­ях потока.

Можно вывести следующие полуэмпирические формулы Прандтля-Никурадзе из логарифмического закона распределения скоростей

Для гладких труб -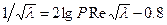

Для вполне шероховатых труб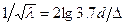

Предложенная полуэмпирическая теория не отражает особенностей сопротивления в области смешанного трения.

Опыты Никурадзе проводились в трубах с одной искусственной шероховатостью. Трубы же, применяемые на практике, имеют шероховатость неоднородную и неравномерную. Поэтому долгое время оставалось неясным, насколько правильны будут выводы, полученные Никурадзе на трубах с искусственной шероховатостью, в применении к обычным промышленным трубам с естественной шероховатостью и каковы численные значения ше­роховатости для подобных труб, Выяснению этих вопросов был по­священ ряд проведенных экспе­риментальных исследований (работы Кольбрука, И.А.Исаева, ГА.Мурина, ФА Шевелева).

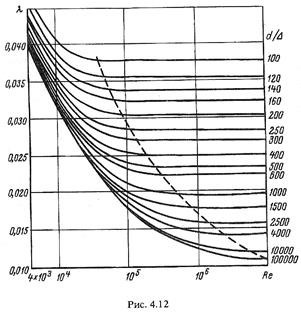
Наибольший интерес представляют опыты ГА.Мурина по исследованию гидравлических сопротивлений в обычных промышленных стальных трубах, законченные в 1948 г. Результаты этих опытов представлены на графике, изображенномрис. 4,12, показывающем изменение коэффициента λ в зависимости от числа Рейнольдса для стальных труб.

Подтвердив основные закономерности, установленные Никурад­зе, эти опыты показали, что для труб с естественной шероховатостью коэффициент λ в пере­ходной области имеет всегда большие значения, чем в случае вполне шероховатых труб (а не меньше, как у Никурадзе), Поэтому кривые на диаграмме Мурина не имеют впадины, характерной для кривых Никурадзе.

Результаты обобщения большого числа опытов показали, что λявляется функцией двух безразмерных параметров числа Рейнольдса­, отражающего влияние вязкости и скорости движения жидкости и относительной шероховатости ε=∆/d, характеризующего влияние поверхности стенок, т.е.

λ=f(Re, ∆/d)

Основные расчетные формулы.

Таблица для определения коэффициента гидравлического трения

Местные сопротивления

Местными сопротивлениями называются, в отличие от сопротивлений по длине, сосредоточенные на коротких участках трубопровода потери напора, вызванные местным отрывом вихрей, а также нарушением структуры потока. Эти процессы в значительной степени зависят от формы местных сопротивлений. Условно местные сопротивления можно разделить на несколько видов, представленных на рис. 4.13

D₁v₂

Внезапное расширение Внезапное сужение

Диффузор Конфузор

Диафрагма Закругление трубопровода

К местным сопротивлениям, в частности, относятся участки трубопроводов, имеющих переходы с одного диаметра на другой, колена, раструбы, тройники, крестовины, всякого рода запорные устройства и приспособления (краны, задвижки, вентили, клапаны), а также фильтры, сетки, специальные устройства входа и выхода к насосам (диффузоры, конфузоры).

Учет местных сопротивлений играет решающую роль при расчете гидравлически коротких трубопроводах, где величина потерь энергии на местных сопротивлениях сравнима с потерями по длине. Практически любое местное сопротивление приводит к

резкому изменению характера течения, сопровождаемого изменением местных скоростей как по величине, так и по направлению.

Нa практике для определения потерь энергии на местных сопротивлениях применяется формула Вейсбаха, выражающая потери в долях скоростного напора

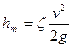, где неизвестный коэффициент пропорциональности ζ называется коэффициентом местного сопротивления.

В качестве скорости v принимается скорость на участке трубопровода, либо до него. От этого будет зависеть численное значение коэффициента ζ, поэтому необходимо специально оговаривать, по отношению к какой скорости вычислен коэффициент местного сопротивления. В общем случае коэффициент ζ зависит от геометрической формы местного сопротивления и числа Re.

Коэффициент ζ принимается постоянным для данного вида местного сопротивления. Однако экспериментальные исследования показали, что это условие соблюдается только при больших числах Рейнольдса (Re> 10⁴), При небольших величинах Re значения коэффициента ζ существенно зависит от числа Рейнольдса, Справочные значения ζ относятся к случаю, когда местное сопротивление работает в условиях автомодельности по числу Re, т.е. не зависит от его числового значения. Значения ζ, приводимые в справочниках, следует считать ориентировочными. Для уточнения данных о конкретном местном сопротивлении необходимо провести экспериментальное исследование в требуемом диапазоне чисел Re. Однако, есть случаи, когда величина потерь энергии на местном сопротивлении может быть определена теоретически, например, при внезапном расширении потока.

Иногда местные сопротивления выражают через эквивалентную длину прямого участка трубопровода . Эквивалентной длиной называют такую длину прямого участка трубопровода данного диаметра, потери напора в котором при пропуске данного расхода равны рассматриваемым местным потерям.

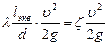, получаем ,или .

Эта формула позволяет весьма просто оценивать роль потерь удельной энергии в местном сопротивлении по сравнению с потерями по длине в общем балансе потерь.