Одномерная линейная регрессия

Пример 1. Функция ТЕНДЕНЦИЯ.

а) Предположим, что фирма желает приобрести земельный участок в июле. Фирма собирает информацию о ценах за последние 6 месяцев, начиная с марта, на типичный земельный участок. Номера месяцев с 1 по 6 (известные значения х) записаны в ячейки В1...G1 – рисунок 4.3.

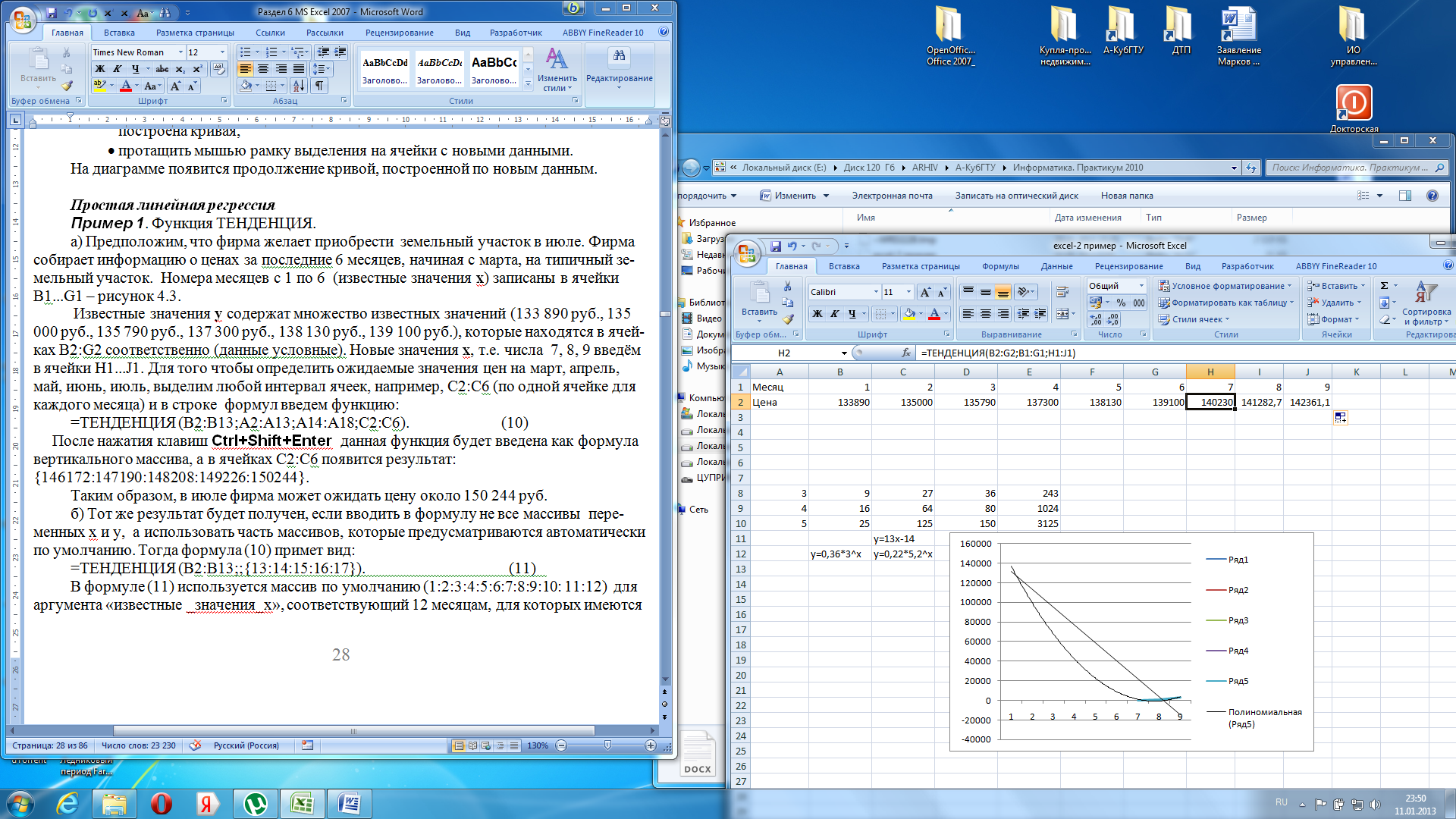
Рисунок 4.3 – Функция Тенденция

Известные значения y содержат множество известных значений (133 890 руб., 135 000 руб., 135 790 руб., 137 300 руб., 138 130 руб., 139 100 руб.), которые находятся в ячейках В2:G2 соответственно (данные условные). Новые значения х, т.е. числа 7, 8, 9 введём в ячейки H1...J1. Для того чтобы определить ожидаемые значения цен на июль, август, сентябрь, выделим любую ячейку, например, H2 и в строке формул введем функцию:

=ТЕНДЕНЦИЯ (В2:G2;B1:G1;H1). (10)

После нажатия клавишbOK в ячейке Н2 появится результат: 140230руб. Далее нужно ухватить мышью за маркер копирования (чёрный квадратик справа внизу в рамке ячейки Н2) и протащить рамку на ячейки I2, J2 – в них тоже появится результат прогнозирования цен на 8 и 9 месяцы.

Таким образом, в августе фирма может ожидать цену около 142361,1 руб.

б) Тот же результат будет получен, если вводить в формулу не все массивы переменных х и у, а использовать часть массивов, которые предусматриваются автоматически по умолчанию. Тогда формула (10) примет вид:

=ТЕНДЕНЦИЯ (В2:G2;;H1:G1). (11)

В формуле (11) используется массив по умолчанию (1:2:3:4:5:6) для аргумента «известные _значения_х», соответствующий 6 месяцам, для которых имеются данные по продажам. Он должен был бы быть помещен в формуле(11) между двумя знаками ;;.

Массив (H1:G1) соответствует следующим 3 месяцам, для которых и получен массив результатов (140230:141282,7:142361,1).

Пример 2 а) Функция ЛИНЕЙН. Дана таблица изменения температуры в течение шести часов, введенная в ячейки D2:E7 (табл. 4.3). Требуетсяопределитьтемпературувовремявосьмогочаса.

Таблица 4.3

	...	D	E
		х -№ часа	у -t○, град.

Выделим ячейки D8:E12 для вывода результата (в соответствии с табл. 3), введём в строку ввода формулу =ЛИНЕЙН(E2:E7;D2:D7;1;1), нажмём клавиши Ctrl+Shift+Enter, в выделенных ячейках появится результат:

Таблица 4.4

3,1428571	-3,3333333
0,5408484	2,106302
0,8940887	2,2625312
33,767442
172,85714	20,47619

Таким образом, коэффициент m =3,143 со стандартной ошибкой 0,541, а свободный член b = -3,333 со стандартной ошибкой 2,106, т.е. функция, описывающая данные табл. 2, имеет вид

у =3,143∙х -3,333 (12)

Тогда при х = 8 получим: у = 3,143∙8 – 3,333 = 21,81^○С.

Стандартные ошибки показывают максимально возможное отклонение параметра от рассчитанной величины . Для у оно составляет 2,263, т.е. реальное значение у может лежать в пределах у±2,263. Таким образом, при х = 8 величина у = 21,81±2,263 град.

Точность приближения к табличным данным (коэффициент детерминированности r²) cоставляет 0,894 или 89,4%, т.е. можно утверждать, что на 89,4% уравнение (12) точно соответствует таблице 3. Это является высоким показателем.

б)Тот же результат можно получить, использовав функцию =ТЕНДЕНЦИЯ (E2:E7;;G2:G5) для, например, следующих четырёх часов, предварительно введя в ячейки G2:G5 числа с 7 до 10. Выделив ячейки Н2:Н5, введя в строку формул эту функцию и нажав Ctrl+Shift+Enter , получим в выделенных ячейках массив {18,667; 21,80952; 24,95238; 28,09524}, т.е. для восьмого часа значение у = 21,809 ≈21,81град.

в) Функция ПРЕДСКАЗ – позволяет предсказывать значение у для нового значения х по известным значениям хиу, используя линейное приближение зависимости у = f(x). Синтаксис функции:

=ПРЕДСКАЗ(нов,_знач._х; изв._знач._ у;изв._ знач._х)

Для данных примера 2 ввод формулы =ПРЕДСКАЗ(8;E2:E7;D2:D7) выводит в заранее выделенной ячейке результат 21,809. Новое значение х может быть задано не числом, а ячейкой, в которую записано это число.

Отличие функции ПРЕДСКАЗ от функции ТЕНДЕНЦИЯ заключается в том, что ПРЕДСКАЗ прогнозирует значение функции линейного приближения только для одного нового значения х.

Экспоненциальная регрессия

Пример 3. а) Функция ЛГРФПРИБЛ. Условие примера 2.

Поскольку функция в табл. 2 носит явно нелинейный характер, целесообразно искать её приближение в виде не прямой линии, как в примере 2, а в виде нелинейной кривой. Из всех видов нелинейности (гипербола, парабола и др.) Excel реализует только экспоненциальное приближение вида у = b∙m^xc помощью функции ЛГРФПРИБЛ, которая рассчитывает для этого уравнения значения b и m. Функция ЛГРФПРИБЛ запускается точно также, как и функция ЛИНЕЙН.

Выделим для результата блок ячеек F8:G12, введём в строку формул функцию =ЛГРФПРИБЛ(E2:E7;D2:D7;1;1), нажмём клавиши Ctrl+Shift+ Enter, в выделенных ячейках появится результат – табл. 4.5:

Таблица 4.5

1,56628015	1,196513
0,02038299	0,07938
0,99181334	0,085268
484,599687
3,52335921	0,029083

Таким образом, коэффициент m = 1,556, а b = 1,197, т.е. уравнение приближающей кривой имеет вид :

у = 1,197∙(1,556 ^х) (13)

со стандартными ошибками для m, b и y равными 0,02, 0,07 и 0,08 соответственно. Коэффициент детерминированности r² = 0,992, т.е. полученное уравнение даёт совпадение с табличными данными с вероятностью 99,2%.

Поскольку интерполяция табл. 2 экспоненциальной кривой даёт более точное приближение (99,2%) и с меньшими стандартными ошибками для m,b и y, в качестве приближающего уравнения принимаем уравнение (13).

При х = 8 получим у = 1,197∙34,363 = 41,131± 0,085^○С.

б) Функция РОСТ вычисляет прогнозируемое по экспоненциальному приближению значения удля новых значений х , имеет формат:

=РОСТ(изв_знач_у;изв_знач_х;нов_знач_х;константа).

Выделим блок ячеек F14:F17, введём формулу

=РОСТ(E2:E7;D2:D7;G2:G5;ИСТИНА), в выделенных ячейках появится массив чисел {27,6696434; 43,3384133; 67,8800967; 106,319248}, т.е. при х=8 значение функции у = 43,34град. Это значение немного отличается от вычисленного в п. а), поскольку функция РОСТ использует для расчетов линию экспоненциального тренда.

Примечание. При выборе экспоненциальной приближающей кривой следует учитывать, что интерполировать ею можно только участки, где функция монотонно возрастает или убывает (при отрицательном аргументе х), т.е. функцию, имеющую точки перегиба (например, параболу, синусоиду , кривую рис. 4.2 и др.) следует разбить на участки монотонного изменения от одной точки перегиба до другой и каждый участок интерполировать отдельно. Для рис. 4.2 функцию нужно разбить на 3 участка.