Числовые и точечные промежутки

1. Пример, имеющий важные применения, – соответствие между множеством действительных чисел R и множеством точек числовой прямой, т.е. прямой, на которой выбраны начало отсчета (ему сопоставлено число 0) и масштаб, однозначно определяющий равномерную шкалу. Каждой точке прямой соответствует ровно одно действительное число – координата этой точки, и обратно, каждому действительному числу x сопоставляется точка прямой с координатой x. Точка, соответствующая большему числу находится правее, меньшему числу – левее. Данное соответствие позволяет множество чисел интерпретировать на геометрическом языке как множество точек прямой.

Пример числовых множеств (т.е. множеств чисел) специального вида – числовые промежутки. Множество чисел A = {x: a < x < b}, расположенных в промежутке между числами
a и b, обозначается (a, b) и называется открытым промежутком, или интервалом. Множество
B = {x: a ≤ x ≤ b} обозначается [a, b] и называется замкнутым промежутком, или отрезком. Концы промежутка принадлежат отрезку, но не принадлежат интервалу. Аналогично определяются полуинтервалы [a, b), (a, b] (один конец принадлежит промежутку, другой - не принадлежит), а также бесконечные промежутки (–¥, b], [a, +¥), (–¥, b), (a, +¥).

Окрестностью точкиназывается любой интервал, содержащий эту точку, ε-окрестность точки x – симметричный интервал (x–ε, x+ε).

Пример.Пусть A, B, C – множества действительных чисел: A = (–4, 7); B = [0, 10], C = [–1, 4). Числовые промежутки A, B, C изображены на рис. 2.3. Светлыми кружками обозначены концы промежутка, не принадлежащие ему (так, у интервала оба конца – светлые); закрашенными – принадлежащие промежутку.

Рис. 2.3

Тогда A ∩ B = [0, 7); A È B = (–4, 10]; A \ B = (–4, 0); B \ A = [7, 10]; C \ A = Æ; A \ C =
= (–4, –1) È [4, 7).

Упражнение. Покажите на числовой прямой множества B ∩ C, B È C, B \ C, C \ B, A ∩ C,
A È C и представьте эти промежутки с помощью введенных выше обозначений.

Замечание. Следует отметить, что одинаковым образом определяются и обозначаются числовые промежутки как в области действительных чисел (и тогда промежуток содержит бесконечное множество чисел), так и в области целых чисел (тогда, например, целочисленный отрезок [–3, 2] содержит 6 чисел: {–3, –2, –1, 0, 1, 2}, а интервал (-3, 2) содержит 4 числа:
{–2, –1, 0, 1}.

2. Более сложный пример – соответствие между точками плоскости с прямоугольной (декартовой) системой координат и упорядоченными парами действительных чисел (т.е. пары
(3, 5) и (5, 3) считаются различными). Каждой точке плоскости соответствует пара чисел –
ее координаты: абсцисса x и ордината y. Обратно, каждой паре чисел соответствует единственная точка с такими координатами. Поэтому плоскость можно рассматривать как прямое произведение R ´ R = R². Множество точек, которое можно назвать геометрической фигурой, может быть
задано аналитическим условием, связывающим координаты этих точек. Такое соответствие служит основанием методов аналитической геометрии на плоскости. Например, множество
D = {(x, y): a < x < b, c < y < d} состоит из внутренних точек прямоугольника (рис. 2.4).

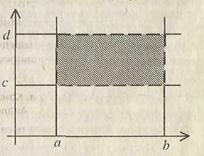
Рис. 2.4

Обычно, если условие, определяющее множество точек плоскости, является равенством, связывающим переменные величины x и y, то это множество представляет собой кривую линию на плоскости. Так, множество

C = {(x, y): x² + y² = 25} (*)

состоит из точек, находящихся на расстоянии 5 от начала координат, т.е. является окружностью радиуса 5. Множество, задаваемое условием K = {(x, y): x² + y² ≤ 25}, представляет собой внутренность круга радиуса 5, включая граничную окружность (поскольку неравенство
в условии – нестрогое).

Замечание. Проверьте, что если в условии (*), задающем множество C, число 25 заменить числом 0, то множество C будет состоять из одной точки (0, 0), а если заменить его отрицательным числом (–1), то C будет пустым множеством.

Пример. Рассмотрим два множества точек на плоскости A = {(x, y): y ≤ x}, B = {(x, y): x < 2} (рис. 2.5).

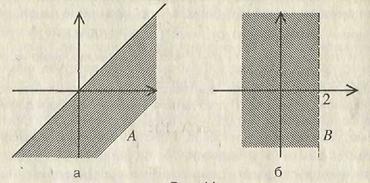
Рис. 2.5

Первое множество состоит из всех точек, ордината которых меньше или равна абсциссе. Точки, для которых выполнено равенство x = y, образуют биссектрису 1-го и 3-го координатных углов. Точки множества А - полуплоскость, расположенная ниже (в данном случае можно сказать: правее) этой биссектрисы (рис. 2.5, а). Множество В состоит из точек, абсцисса которых строго меньше 2, а ордината – любое число. Эти точки составляют полуплоскость, расположенную левее вертикальной прямой, проходящей через точку 2 на оси ОХ (рис. 2.5, б). Тогда каждое из множеств A ∩ B, A È B, A \ B, B \ A представляет собой множество точек, заполняющих некоторый угол, образованный этими прямыми (рис. 2.6, а, б, в, г).

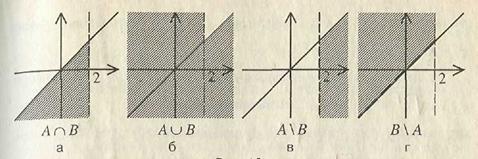
Рис. 2.6

3. Пусть y = f(x) – числовая функция переменной x. Тогда множество G = {(x, y): y = f(x)} состоит из точек плоскости, первая координата которых принимает значения из области определения функции, т.е. допустимые значения аргумента x, а вторая координата равна соответствующему значению функции y = f(x). Множество G представляет собой графикфункции: каждому допустимому значению аргумента соответствует ровно одна точка плоскости.

Суперпозиция функций

1. Функция n переменных (n-местная функция)– это соответствие типа

A₁´ A₂ ´ . . . ´ A_n → B (другая форма записи: f(a₁, a₂, . . . , a_n) = b,

где a_i Î A, b Î B). Сложение, вычитание, умножение, деление, возведение в степень являются двуместными функциями: W = x + y, W = x - y, W = x • y, W = x / y, W = x^y. Двуместными функциями являются также max(x, y) и min(x, y):

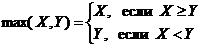
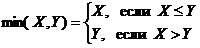
Пример. max (3, -2) = 3; min (3, -2) = -2; max (3, 3) = 3.

Функции обычно задаются вычислительными процедурами, позволяющими по значению аргументов определить значение функции. Форма этих процедур может быть различной: формулы, графики, таблицы.

В понятии формулы важным элементом является операция подстановки, или суперпозиции, позволяющая из одних функций получать другие.

Если в функцию f(X) подставить вместо аргумента Х функцию g(X), получается суперпозиция (или сложная функция) f(g(X)). В этой суперпозиции f(X) – внешняя функция, g(X) – внутренняя. Допускается также переименование переменных.

Пример. Cуперпозицией внешней функции f(x) = sin x и функции g(x) = x² является функция f(g(x)) = sin (g(x)) = sin(x²); если же внешняя функция g(x), а внутренняя f(x), то суперпозицией g(f(x)) будет (f(x)² = (sin x)² = sin²x.

Функции в суперпозиции могут быть не только одноместными.

Суперпозиция функций – функция, полученная из n-местной функции f(x₁, x₂,..., x_n) и системы n функций g₁, g₂,..., g_n некоторой подстановкой функций g₁, g₂,..., g_n во внешнюю функцию f вместо переменных и переименованиями переменных.

Примеры.1. Cуперпозициями внешней функции f(X,Y) = X / Y и функций g₁(X) = 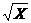и
g₂(X) = a^X являются: функция 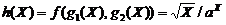, или функция 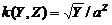, или функция 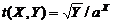, или функция .

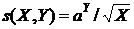Более сложные суперпозиции этих функций: , .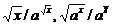

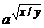2. Примером суперпозиции одноместной функции Y = X, нульместных функций Y = const и двуместных функций Z = X + Y и Z = X ∙ Y является многочлен

.

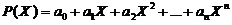3. Суперпозициями двуместных функций min(X, Y) и max(X, Y) являются функции
трех переменных min(X, max(Y, Z)), min(X, min(Y, Z)), max(X, min(Y, Z)), max(X, max(X, Y)).

4. Класс элементарных функций есть множество всех суперпозиций основных элементарных функций (к ним относятся одноместные: степенные – х^α, показательные – а^х, логарифмические – log_а x, тригонометрические и обратные тригонометрические, а также константы) и двуместных функций, представляющих арифметические операции: x + y, x - y, x • y, x / y.

Класс элементарных функций можно рассматривать как результат порождающей процедуры, в которой используются, исходя из основных элементарных функций, четыре арифметических действия и операция подстановки.

Замечание. Среди основных элементарных функций нет двуместной функции Z = X^Y.
Ее можно выразить суперпозицией других функций: логарифмической S = lg X, показательной T = 10^X и умножения – в силу тождества X^Y = 10^Y•lgХ.

Как видно из примеров, в суперпозиции функций могут измениться как сами переменные, так и их число. Заметим также, что, выполняя подстановки, мы преобразовываем формулы, выражающие функции. Формула – это выражение, описывающее суперпозицию и содержащее функциональные знаки, символы независимых переменных (аргументов) и констант (параметров). Формула с использованием скобок определяет порядок действий при вычислении значения функции. Специальные договоренности, позволяющие упростить вид формулы, освобождают ее от некоторых скобок: так в арифметике принято, что умножение и деление связывают сильнее, чем сложение и вычитание, и одночленные сомножители не заключаются в скобки.

2. Рассмотрим еще один пример функционального соответствия. Пусть U – универсальное множество; M – некоторое его подмножество, B = {0, 1} – множество из двух чисел 0 и 1.

Характеристической функцией множества M Í U – называется отображение χ_M: U → B, ставящее в соответствие элементам множества M единицу, а элементам дополнения 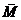– ноль.

Примеры. 1. В множестве целых чисел Z для подмножества А квадратов целых чисел
(A = {x: x = k²}) имеем: χ_А(4) = χ_А(25) = = 1, χ_А(5) = χ_А(12) = 0; для подмножества В четных чисел (В = {x: x = 2k}) имеем: χ_В(4) = χ_В(12) = 1, χ_В(5) = χ_В(25) = 0.

2. В множестве натуральных чисел U = [0, 7] для множества М = {1, 3, 6} график функции
χ_М - на рис. 2.7

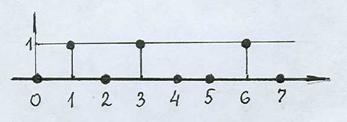
Рис. 2.7

Легко проверяются следующие свойства характеристической функции множеств, получаемых из множеств M, N операциями пересечения, объединения, разности и дополнения:

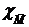= 1 - χ_M; χ_{M ∩ N} = χ_M • χ _N ; χ_{M È N} = χ_M + χ _N - χ_M • χ _N ; χ_{M \ N} = χ_M - χ_M • χ _N .

Булеаном В(U)называется множество всех подмножеств множества U.

Если U - конечное множество, ½U½ = n, и его элементы занумерованы числами 1, 2,..., n, то каждому подмножеству M Í U соответствует n-мерный вектор из нулей и единиц с компонентами χ_M(e_n), где χ_M – характеристическая функция множества М. Совокупность всех таких характеристических векторов можно рассматривать как множество точек n-мерного арифметического пространства с координатами 0 или 1. Вместе они образуют n-мерный единичный куб.

Если U – конечное множество и число его элементов ½U½ равно n, то число элементов булеана В(U) равно числу 2ⁿ характеристических векторов. Подробнее об этом – в разделе «Элементы комбинаторики» Юниты 2.