Операции над множествами: пересечение, объединение, разность, дополнение

1. Для задания множеств применяется еще один способ – с помощью теоретико-множественных операций, позволяющих строить из одних множеств другие. Рассмотрим несколько таких операций и их представления диаграммами Венна.

A. Пересечением двух множеств A и B называется множество М = A ∩ B, состоящее из элементов, принадлежащих обоим множествам: и множеству A, и множеству B. Пересечение – это общая часть двух множеств (область D на рис. 1.2). Аналогично определяется пересечение
трех или более множеств (показано частой штриховкой на рис. 1.3). Символ ∩ означает операцию пересечения множеств.

Термин «пересечение» – по существу геометрического происхождения. Пересечением прямой и плоскости, если прямая не лежит на плоскости и не параллельна ей, является их единственная общая точка. Если прямая и плоскость параллельны, то их пересечение не содержит ни одной точки, т.е. пусто. Если же прямая имеет с плоскостью более одной общей точки, то, как известно, она целиком лежит на плоскости, и их пересечение совпадает с множеством точек этой прямой.
В этом случае множество точек прямой есть подмножество множества точек плоскости.

B. Объединением двух множеств A и B называется множество М = A È B, состоящее из всех элементов, принадлежащих хотя бы одному из множеств A или B (или обоим). При этом каждый элемент входит в объединение один раз. Символ È означает операцию объединения множеств (области С, D, E вместе на рис. 1.2). Объединение трех и более множеств определяется аналогично (показано редкой штриховкой на рис. 1.3).

C. Разностью М = A \ B двух множеств A и B называется множество, состоящее из всех элементов A, не принадлежащих B. Иначе говоря, чтобы получить разность, нужно из множества A удалить его общие элементы с множеством B (на рис. 1.2 разность A\B=C ). Разность B \ A – область E на рис. 1.2.

D. Симметрическая разность – М = АΔВ - множество элементов, которые принадлежат ровно одному из двух множеств A и B (можно рассматривать как объединение двух разностей): АΔВ = (A\B) È (B\A). На рис. 1.2 АΔВ = С È Е.

Симметрическую разность называют также суммой по модулю 2. Очевидно соотношение: АΔВ = (A È В) \ (A ∩ B).

На рис. 1.4 – частные случаи общей картины, изображенной на рис. 1.2.

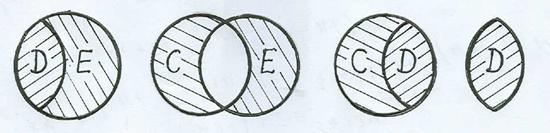
а) б) в) г)

Рис. 1.4

Если С = A \ B = Æ, т.е. A Í B, то D = A, E = B \ A, (рис. 1.4, а).

Если D = A ∩ B = Æ, то С = A, E = B (рис. 1.4, б).

Если E = B \ A = Æ, т.е. B Í A, то С = A \ B, D = B (рис. 1.4, в).

При равенстве множеств A и B и имеем C = E = Æ, D = A = B, (рис. 1.4, г).

E. Пусть A – некоторое множество в универсальном множестве U. Дополнением 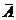множества A называется множество, состоящее из всех элементов множества U, не принадлежащих A. Иными словами, 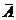= U \ A (рис. 1.5).

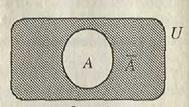
Рис. 1.5

Примеры. 1. Пересечением множества 5-этажных домов и множества кирпичных домов является множество кирпичных пятиэтажек.

2. Пусть в множестве учеников школы (оно будет служить универсальным множеством U) A – подмножество учащихся, занимающихся спортом; B – подмножество учащихся, интересующихся музыкой; C – подмножество мальчиков. Тогда пересечению A ∩ B принадлежат все учащиеся, увлекающиеся и спортом, и музыкой; в пересечение A ∩ C входят мальчики, увлекающиеся музыкой; объединение A È B – множество учащихся, увлекающихся или спортом, или музыкой, или тем и другим; дополнение – множество школьниц; разность C \ B – множество мальчиков, не интересующихся музыкой; разность B \ C – множество девочек, увлекающихся музыкой.

3. Пусть множество натуральных чисел A = {1, 2, 3, 4, 6, 8, 12, 24} – делители числа 24;
B = {1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90} – делители числа 90. Тогда пересечение
A ∩ B = {1, 2, 3, 6} – множество общих делителей этих чисел (6 – наибольший общий делитель).

С помощью введенных операций можно образовывать более сложные комбинации. Например, формула (A \ B)∩ C представляет множество элементов множества A, не принадлежащих B, но принадлежащих C (рис. 1.6); множество A È (B ∩ C) содержит все элементы, которые принадлежат A, а также общие элементы множеств B и C (рис. 1.7).

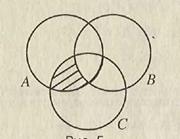
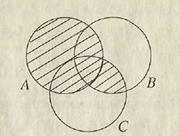
Рис. 1.6 Рис. 1.7

Упражнение. Сформулируйте словами, какие подмножества универсального множества U учеников школы (пример 2) представляются формулами , C \ (AÈ B), (A ∩ B) \ .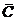

2. На диаграммах Венна легко проверить соотношения:

A ∩ B Í A Í A È B;

A \ B Í A Í A È B;

(АΔВ) ∩ (А ∩ B) = Æ;

если A \ B = Æ , то A Í B;

если A и B – конечные множества, то ½A È B½= ½А½+ ½B½ – ½А ∩ B½, в частности, если
A ∩ B = Æ, то A È B = ½А½+ ½B½, поскольку ½Æ½ = 0.

Перечислим основные свойства операций над множествами. Пусть U – универсальное множество, A, B, C – его подмножества, Æ – пустое множество. Равенства 1–10, 15–18 относятся к операциям объединения и пересечения; равенства 11–14 и 19–21 – к операции дополнения.

1. A È B = B È А 2. A ∩ B = B ∩ A

3. (A È B) È C = A È (B È C) 4. (A ∩ B) ∩ C = A ∩ (B ∩ C)

5. (A È B) ∩ C = (A ∩ C) È (B ∩ C) 6. (A ∩ B) È C = (A È C) ∩ (B È C)

7. A È A = A 8. A ∩ A = A

9. A È (A ∩ B) = A 10. A ∩ (A È B) = A

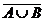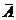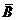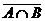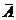11. = ∩ 12. = È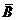

13. A È 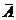= U 14. A ∩ 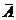= Æ

15. A È Æ = A 16. A ∩ Æ = A

17. A È U = U 18. A ∩ U = A

19. 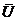= Æ 20. 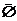= U

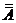21. = A

Свойства 1, 2 – переместительные законы, свойства 3, 4 – сочетательные законы. Свойства
5, 6 – взаимные распределительные законы каждой из операций ∩, È относительно другой. Свойства 11, 12 называются законами де Моргана для множеств (дополнение к объединению равно пересечению дополнений; дополнение к пересечению равно объединению дополнений). Свойства 13 – 20 - соотношения с универсальным и пустым множествами.

Приведем также некоторые свойства операции разности множеств: A \ B = A ∩ 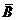; A \ A = Æ;
A \ Æ = A; A \ U = Æ; U \ A = .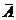

3.Разбиение множества A – такая система {B_α} непустых подмножеств множества A, что все попарные пересечения – пусты (B_i ∩ B_j = Æ, если i ≠ j – это свойство называется чистотой разбиения), а их объединение ÈB_α равно A (это называется полнотой разбиения). Сами
B_α называются классами, или блоками разбиения.

При анкетировании или классификации объекты распределяются по группам; не входящие в ту или иную конкретную группу, могут составлять группировку «прочие» – для полноты разбиения.

Система курсов данного факультета есть разбиение множества его студентов; система групп есть другое разбиение того же множества. Другой пример: множество всех автомобилей может быть разными способами разбито на классы в зависимости от назначения: транспортные, специальные и гоночные; в свою очередь, транспортные автомобили подразделяются на легковые, грузовые и автобусы. Возможно разбиение в зависимости от марки, объема двигателя, года выпуска, компании-производителя, стоимости и др.

Множество квартир дома разбивается на подмножества квартир, расположенных на одном этаже; другое разбиение – на подмножества квартир из одного подъезда.

Множество R действительных чисел разбивается на множество рациональных и множество иррациональных чисел; множество Z целых чисел разбивается на множество четных и множество нечетных чисел.

Множество прямых на плоскости разбивается на бесконечную совокупность систем прямых, параллельных тому или иному направлению.

Замечание. В последнем примере элементами являются не точки плоскости, а прямые. Поэтому, например, пересечение любого множества горизонтальных прямых и любого множества вертикальных прямых пусто: ведь ни одна прямая не является одновременно горизонтальной и вертикальной.

Если A и B – два подмножества универсального множества U, то 4 подмножества D₀ = 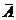∩ 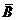, D₁ = 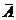∩ B, D₂ = A ∩ 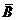, D₃ = A ∩ B образуют разбиение множества U (рис. 1.8). Поэтому, если
U - конечное множество, то для числа элементов множества и блоков разбиения выполнено равенство ½U½ = ½D₀½+ ½D₁½+ ½D₂½+ ½D₃½.

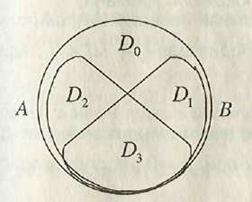
Рис. 1.8

Аналогично, для трех множеств A, B, C разбиение универсального множества U на восемь подмножеств M₀ - M₇ изображено на рис. 1.9. Сами множества A, B, C могут быть представлены как объединения:

A = M₄ È M₅ È M₆ È M₇;

B = M₂ È M₃ È M₆ È M₇;

C = M₁ È M₃ È M₅ È M₇.

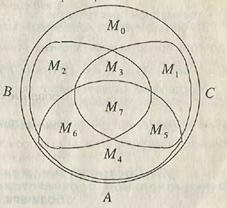
Рис. 1.9

Упражнение. Выразить множества M₁ - M₇ с помощью операций È, ∩, ‾‾ над множествами A, B, C.

Указание: множество M₀, например, можно представить так: M₀ = .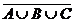

Замечание. Стоит заметить, что возможно и другое представление: M₀ = 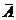∩ ∩ 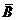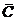(равенство этих двух формул – обобщение закона де Моргана).

Порождающая процедура

Еще один способ задания множества связан с понятием порождающей процедуры: множество состоит из всех элементов, которые могут быть получены некоторой последовательностью операций из заданной конечной системы.

Простейший пример – задание последовательности элементов множества формулой, содержащей параметр: A = {X_k = 3 + 2(k² + 1)}, k = 0, 1, 2,...

Задавая различные значения параметра k, мы можем вычислять элементы множества
A: X₀ = 5, X₁ = 7, X₂ = 13 и т.д. Подобное задание может быть явным, как в данном примере, или неявным, требующим разрешения. В частности, могут использоваться возвратные, или рекуррентные соотношения, когда одни элементы множества определяются через другие.

Примеры: 1. Арифметическая прогрессия определяется заданием ее первого члена а₁, разности прогрессии d и соотношением а_n+1 = а_n + d для n ≥ 1. Рекуррентная формула позволяет вычислять значения а₂ = а₁ + d, а₃ = а₂ + d = а₁ +2d, а₄ = а₃ + d = а₁ + 3d и т.д. Можно выразить
n-й член прогрессии в явном виде: а_n = а₁ + d • (n – 1).

2. Геометрическая прогрессия определяется заданием ее первого члена b₁, знаменателя прогрессии q и соотношением b_n+1 = b_n • q для n ≥ 1. Можно последовательно вычислять значения b₂ = b₁ • q, b₃ = b₂ • q = b₁ • q², b₄ = b₃ • q = = b₁ • q³ и т.д.; n-й член этой последовательности выражается явно: b_n+1 = b₁ • qⁿ.

3. Последовательность чисел Фибоначчи задается условиями: а₁ = 1, а₂ = 1, а_n = а_n-1 + а_n-2 для
n > 2.

Последняя формула позволяет последовательно вычислять значения а₃ = а₂ + а₁ = 1 + 1 = 2,
а₄ = а₃ + а₂ = 2 + 1 = 3, а₅ = а₄ + а₃ = 3 + 2 = 5, а₆ = а₅ + а₄ = 5 + 3 = 8,... и т.д. Выражение общего
n-го члена этой последовательности в явном виде существует, но более сложно.

Рассмотрим еще один способ задания числового множества M:

(1) 5 Î М;

(2) если а Î М, то 1/ а Î М;

(3) если а Î М, то 1 - а Î М.

Убедимся, что множество М конечно и состоит из 6 элементов, а именно
М = {5, 1/5, -4, -1/4, 4/5, 5/4}. Действительно, для каждого a, начиная со значения a = 5, есть
две возможности порождения новых элементов: операциями (2) или (3). При этом могут получаться и элементы, порожденные ранее. Так, из числа 5 операцией (2) получается 1/5, операцией (3) – число (–4), а из числа 1/5 операцией (2) – снова число 5 и т.д. Рассмотрим схему порождения (рис. 1.10), где операция (2) изображена тонкой стрелкой, а операция (3) – утолщенной. Схема показывает, что никаких других чисел процедуры (2) и (3) не дают.

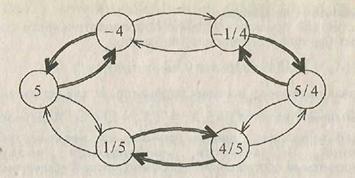
Рис. 1.10

Упражнение. Проследите, какое число в множестве М порождается, начиная с элемента 5, конечной последовательностью операций (2), (3), (3), (2), (2), (3), (2).

Если же, например, в операции (3) заменить (1 – а) на (2 – а), то порождаемое множество будет бесконечным; в частности, из числа 5 чередованием операций (2) и (3) порождается последовательность чисел 5 Þ 1/5 Þ 9/5 Þ 5/9 Þ 13/9 Þ 9/13 Þ 17/13 Þ 13/17 Þ . . .