Алгоритм построения иерархической классификация (дендрограммы)

Приводимый здесь алгоритм построения иерархической классификации основан на анализе значений матрицы сходства. Аналогично проводится построение иерархической классификации на основе меры различия. Рассмотрим пошаговую обработку данных для построения дендрограммы сходства с иллюстрацией ряда процедур на примерах в целях лучшего понимания алгоритма.

Шаг 1. Определяются два множества: множество исследуемых объектов J= {S₁, S₂, ..., S_q} и множество признаков Z = {Z₁, Z₂, ..., Z_p}. Экспертно формируются индексированные множества по каждому объекту. Строится матрица сходства

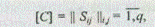
где S_ij — значение меры сходства объекта S_i с объектом S_j;

q — число анализируемых объектов.

Последующую иллюстрацию алгоритма осуществим на примере матрицы сходства {см. табл. 5.6).

Шаг 2. Просматриваются все элементы матрицы сходства [С], расположенные выше главной диагонали. Определяется и метится элемент, имеющий максимальное значение меры сходства С (S_i, S_j)max (данный элемент не принадлежит к элементам главной диагонали). Для рассматриваемой матрицы сходства таким элементом является С (S₄, S₅) = 0,75. Если в матрице сходства более одного элемента с одинаковым максимальным значением, то отбирается и метится любой их них.

Шаг 3. Определяются номера i-й строки j-го столбца, на пересечении которых расположен отмеченныйна шаге 2 элемент. Из матрицы сходства извлекаются все значения, соответствующие i-й строке и j-му столбцу, из которых формируются два массива значений мер сходства:

Hi=Si	S1	S2	S3	S4	S5	S6	S7
С(S4, Si)	0,44	0,60	0		0,75	0,25	0,67
C(S5, Si)	0,55	0,5	0,73	0,75		0,60	0,55

Ш а г 4. Определяется мера сходства классов G (Н, Н^) одним из методов, описываемых обобщенной формулой (5.6). Используем метод медианы. Тогда

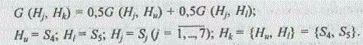
С учетом метода медианы имеем

Hi=Si	S1	S2	S3	S4, S5	S6	S7
С(S4,5, Si)	0,50	0,55	0,37		0,43	0,61

Полученный массив данных вписывается на место четвертой и пятой строк и четвертого и пятого столбцов вновь формируемой матрицы сходства. Наша исходная матрица сходства примет следующий вид:

	S1	S2	S3	S4,5	S6	S7
S1		0,62	0,50	0,55	0,55	0,5
S2	0,62		0,46	0,55	0,50	0,62
S3	0,50	0,46		0,37	0,73	0,33
S4,5	0,50	0,55	0,37		0,43	0,61
S6	0,55	0,50	0,73	0,43		0,36
S7	0,50	0,62	0,33	0,61	0,36

На данном шаге запоминаются значения индексов вновь образованного класса (S_4,5) и меры сходства, при которой этот класс образовался, — С (S₄, S₅) = 0,75.

Шаг 5. Процедура обработки матрицы сходства вновь начинается с шага 2. Итерационный процесс продолжается до тех пор, пока размерность матрицы сходства не уменьшится до 2 х 2. На этом процесс построения иерархической классификации заканчивается.

В результате работы алгоритма определяются перечень индексов классов в том порядке, в котором они объединялись в новые классы, а также уровни сходства, на которых это объединение происходило. Для рассматриваемого примера имеем следующие результаты:

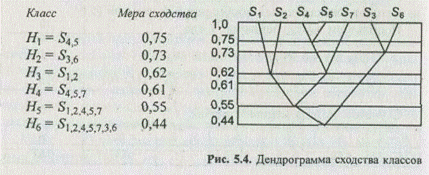
Полученные результаты используются для построения дендрограмм. Дендрограмма делает наглядной структуру иерархической классификации. В данном примере (рис. 5.4) наибольшим сходством обладают классы S₄ и S₅, наименьшим — классы Н₅ = {S₁, S₂, S₄, S₅, S₇} и Н₂= {S₃, S₆}.