В.В. Афанасьев, В.А. Логиновский

В.В. Афанасьев, В.А. Логиновский

Расчет координат места судна по избыточным измерениям

Учебное пособие по математическим основам судовождения

Санкт-Петербург , 2002

УДК 656.61.052:527:62 ББК 39.471.1 А 94

Афанасьев В.В., Логиновский В.А.

А 94 Расчет координат места судна по избыточным навигационным измерениям: Учеб. пособие по математическим основам судовождения. - СПб.: ГМА им. адм. С.0. Ма­карова, 2002. - 40 с.

В учебном пособии рассмотрены теоретические основы определения места судна и линейные методы расчета координат. Дано разъяснение таких основных понятий, как навигационная функция, навигационный параметр, навигационная изолиния, градиент навигационной функции. Изложены вопросы линеаризации навигационных функций, рассмотрены аналитические и графоаналитические методы расчета координат.

Предназначено для курсантов III курса очного и студентов заочного обучения судоводи­тельского факультета.

Рекомендовано к изданию на заседании кафедры судовождения. Протокол № 9 от 30 апреля 2002 года.

Рецензенты:

Трегубов B.C., ст. науч. сотр. (Гос.НИНГИ);

Брусенцов В.П., канд. техн. наук, доц. (Государственная морская академия им. адм. С.0. Макарова).

Введение

Определение координат места судна и оценка их точности являются основными задачами морской навигации. Точное знание координат места судна определяет уровень безопасности плавания и существенно влияет на экономические показатели его работы. В настоящее время задачи определения места решаются как с помощью методов классической навигации, так и автоматизированными средствами, наиболее популярными из которых являются спутниковые навигационные системы. Для повышения точности и надежности определения координат измеряется избыточное число навигационных или радионавигационных параметров. Современные многочисленные алгоритмы расчета координат и оценки их точности по измеренным параметрам строятся на базе классических методов линейной алгебры, основой которых является метод наименьших квадратов (МНК). Линеаризация навигационных функций позволяет построить универсальные и однозначные алгоритмы расчета координат, независимо от измеряемого параметра. Для современного изложения МНК используется математический аппарат матричного исчисления.

Грамотное использование навигационной техники требует от судоводителя знания и понимания как физических, так и математических процессов обработки измеренной информации.

Учебное пособие предназначено для изучения вопросов расчета координаты места судна при избыточных измерениях.

Целью курсовой работы на тему «Расчет координат места судна по избыточным навигационным измерениям» по дисциплине Математические основы судовож­дения (МОС) является изучение основ теории навигационных функций и линейных методов обработки навигационной информации, включая классический вариант с применением современного матричного исчисления.

Работа выполняется на листах бумаги формата А4 и включает две части:

теоретическую и расчетную.

Содержание курсовой работы приведено в прил. 1, образец титульного листа дан в прил.2.

В конце курсовой работы необходимо оставить два чистых листа формата А4, которые будут использоваться при защите.

Вычисления в курсовой работе выполняются с полной разрядной сеткой калькулятора. Если расчет был произведен на компьютере, то при защите работы необходимо показать умение применять использованное программное обеспечение.

Теоретические основы

определения места судна

Глава содержит определения навигационного параметра, навигационной функции, градиен­та навигационной функции, навигационной изолинии, и описания их использования для расчета координат места судна.

Общие сведения

Счисление пути судна с помощью автономных средств навигации (лаг, гирокомпас), кроме важного преимущества, которое заключается в автономности определения счислимых координат, обладает и существенными недостатками. Эти недостатки характеризуются погрешностями курсоуказателей (компасов) и относительных измерителей скорости (лагов). На показания лагов влияют гидрометеорологические факторы (ветер, волнение, течение, качка). Погрешности счисления растут во времени, снижая точность счислимых координат. Для их компенсации применяют внешние измерения, на точность которых указанные факторы влияния не оказывают. С помощью таких измерений можно получить координаты места судна, которые называются обсервованными, а сама процедура получения координат называется обсервацией. Таким образом, координаты места судна могут быть счислимыми и обсервованными. В большинстве случаев обсервованные координаты точнее счислимых, хотя бывает и наоборот.

Для определения обсервованных координат с помощью различных навигационных средств измеряются навигационные параметры (НП).

Градиент навигационной функции - это вектор максимальной скорости изменения НФ в конкретной точке поля навигационных параметров, который направлен по нормали к навигационной изолинии в сторону увеличения НП.

В локальной прямоугольной системе координат g может бьггь представлен в виде двухкомпонентного вектора следующим образом:

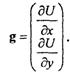
Тогда его модуль рассчитывается по теореме Пифагора:

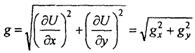
здесь g^, gy - проекции вектора g на координатные оси. Направление вектора^ определится следующим образом:

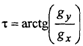
Пояснение формул (1.3) - (1.7) представлено на рис. 1.1.

Равноточные измерения

Число навигационных измерений при определении места судна очень существенно. Если измеряются два навигационных параметра и определяются две координаты, то говорят, что в задаче отсутствует избыточность, т.е. система уравнений (2.6), как правило, совместна.

Отсутствие избыточности измерений приводит к неконтролируемому влиянию различных видов погрешностей на результат, особенно опасны грубые промахи и систематические погрешности.

Для получения более надежной обсервации применяют избыточные навигационные измерения.

Пусть для определения координат измерены три навигационных параметра (п = 3), а определить нужно две координаты (k = 2). В этой ситуации избыточность r= n-k=1.

Первоначально систему уравнений линий положения в матричном виде запишем так же, как систему уравнений (2.6):

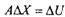
однако матрицы будут иметь вид:

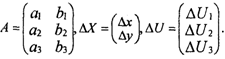
В данной системе количество неизвестных k меньше, чем количество уравнений п. Решение любых двух уравнений дает положение одной из вершин треугольника. Это означает, что подстановка этого решения в третье уравнение, не обратит его в тождеств \ Такая система называется несовместной, т.е. решение пары уравнений не совместно с третьим. Для получения согласованного решения системы необходимо ввести дополнительные условия. Если предположить, что систе­

матические погрешности в изме­рениях отсутствуют, т.е. они определены и исключены специ­альными приемами измерений, то все остальные погрешности изме­рений можно считать случайными. Известно, что центром группиро­вания случайных величин явля­ется их математическое ожидание или его оценка - среднее зна­чение, которое наиболее близко к истинному значению и имеет ми­нимальную дисперсию. Очевидно, что и в данном случае необходимо

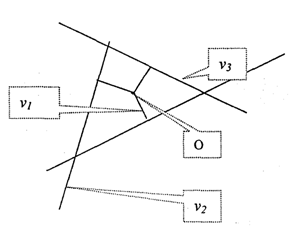
Рис. 2.2. К выводу формулы решения системы уравнений (2.7)

найти некоторое среднее из трех точек, которое будет иметь статус оценки математического ожидания множества, состоящего из трех измерений. Ясно, что эта точка должна быть в фигуре погрешностей, а не вне ее. Несогласованность измерений возникает из-за погрешностей, которые называют невязками системы уравнений.

Теперь вместо системы (2.9), с учетом невязок, более корректно следует записать следующее матричное уравнение (система уравнений поправок):

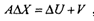
где V- вектор невязок (погрешностей), который имеет вид:

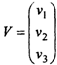
Если принять, что для получения согласованного решения линии положения необходимо сдвинуть внутрь фигуры погрешностей на некоторые величины v/, v^ и уз соответственно (рис. 2.2), то математическое условие поиска оптимального согласованного решения относительно этого среднего значения (точка О) определится в соответствии с формулой (2.11), т.е. минимальной длиной вектора V:

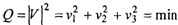
здесь величины v\, v-г. и уз, выраженные в единицах измерений, называются невяз­

ками, поправками или погрешностями измерений в за­висимости от при­даваемого им знака. Выражение (2.11) определяет усло­вие решения сис­темы (2.10), а от­сюда и название рассматриваемого метода — метод наименьших квад­ратов.

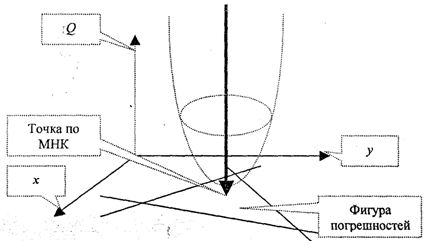
Рис. 2.3. Геометрическая интерпретация МНК

Из формулы (2.10) запишем выражение относительно вектора невязок:

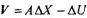
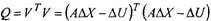
Взяв производную от выражения (2.12) по вектору неизвестных и приравняв ее к нулю, находим формулу для решения системы (2.10):

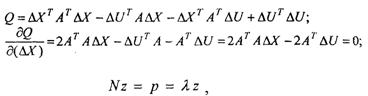
Система (2.13) называется системой нормальных уравнений. Теперь можно записать решение:

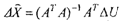
Знак «^л» над вектором искомых величин свидетельствует о том, что решение получено с применением критерия оптимальности Q, Рис. 2.3 поясняет решение по МНК.

После получения решения, согласно выражению (2.14) относительно счислимой точки в локальной системе координат, используется формула (2.8), а затем вьшолняется итерационная процедура. Точка, положение которой определяется вектором Хо, называется ввроятнвйшвй точкой.

Неравноточные измерения

В п. 2.3.1 никак не рассматривался вид погрешности измеряемых навигационных параметров, они считались равноточными, т.е. имеющими одинаковые средние квадратические погрешности т.

В общем случае измерения навигационных параметров не являются равноточными, т.е. их средние квадратические погрешности могут отличаться, что и происходит на практике, если измерения выполнены различными приборами или различными наблюдателями. Естественно, что вероятнейшая точка, полученная по МНК, должна быть ближе к той линии положения, которая точнее, а поэтому уравнивание измерений происходит с учетом их весов - величин, обратно пропорциональных квадратам среднеквадратических погрешностей измерений, которые формируют так называемую весовую матрицу. Методика вывода ничем не отличается от предложенной в п. 2.3.1.

Умножим слева правую и левую части уравнения (2.10) на матрицу W, которая имеет следующий вид:

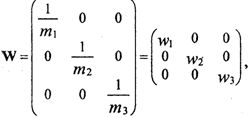
здесь т - средняя квадратическая погрешность измерения соответствующего нави­гационного параметра. Получим следующее уравнение:

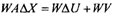
Теперь выражение (2.12) для Q перепишется так:

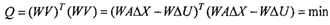
Используя изложенную ранее методику, получим систему нормальных уравнений с учетом неравноточных измерений, предварительно обозначив матрицу H^W-Kav. весовую матрицу D"¹:

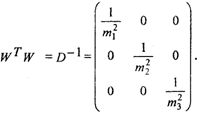
Система нормальных уравнений запишется:

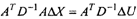
а решение будет иметь вид'

AX=(A^TD~^lA)~^\A^TD~ⁱAU

Если элементы матрицы (2.18) равны, это означает, что измерения равноточные и выражение (2.20) превращается в выражение (2.14). Формула (2.20) имеет более общий характер, чем уравнение (2.14).

Для определения координат опять воспользуемся формулой (2.8). Вероятнейшая точка, полученная по формуле (2.20), определяет средневзве­шенные значения координат.

Графоаналитический расчет

1. На листе миллиметровой бумаги строим систему координат с началом в счислимой точке и выбираем масштаб для прокладки (рис. 2.7).

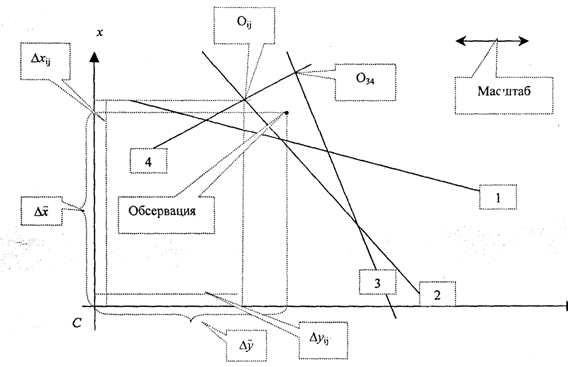
Рис. 2.7. Графоаналитический расчет координат места судна

2. Производим прокладку линий положения, используя формулу Дп, =—'-, и Si

получаем фигуру погрешностей координат.

3. Определяем приращения координат каждой из вершин фигуры погрешностей ау,/, Ауу.

4. Каждая точка пересечения двух линий положения Оу имеет вес, который можно рассчитать по следующей формуле:

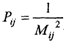
где My — средняя квадратическая погрешность точки по двум линиям положения. 5. Находим средневзвешенное значение приращений координат относительно счислимой точки:

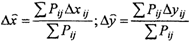
6. Находим обсервованные прямоугольные координаты, используя формулу (2.8), а также географические координаты по формулам, приведенным во второй итерации.

7. Для сравнения сгавим точку по первой итерации на диаграмму графоаналитического расчета.

В.В. Афанасьев, В.А. Логиновский

Расчет координат места судна по избыточным измерениям