Частотные дифференциальные слуховые пороги
Частотная разрешающая способность слуха может быть определена с помощью методов, сходных с методами, которые использовались для определения разрешающей способности слуха по амплитуде.
В первом случае слушателям предъявляются два синусоидальных сигнала одинаковой интенсивности и одинаковой частоты, а затем просят изменять частоту одного из сигналов до тех пор, пока они не почувствуют разницу в высоте этих двух сигналов.
Во втором случае разрешающая способность по частоте определяется путем прослушивания частотно-модулированных сигналов - по минимально заметным на слух изменениям частоты. В качестве частоты модуляции здесь также используется частота 4 Гц.
Установлено, что частотная разрешающая способность человеческого слуха, также как и амплитудная, зависит и от частоты, и от интенсивности звукового сигнала.
На рис. 4 показано, как изменяется разрешающая способность слуха по частоте в зависимости от того к какому диапазону частот принадлежит рассматриваемый сигнал. По оси абсцисс здесь отложена частота fисследуемого сигнала, по оси ординат – минимально различимое слухом изменение частоты этого сигнала Δf/f, где Δf- девиация частоты, т.е. отклонение ее от исходного значения в ту или иную сторону. Следует отметить, что при частотной модуляции тоном частота синусоидального сигнала изменяется от величины f –Δf до величины f +Δf, т.е. амплитуда изменений частоты исследуемого сигнала составит 2Δf. На рис. 4 представлено четыре кривые, соответствующие разным значениям уровня исследуемого тона.
| 1к |
| 4к |
| 2к |
| 8к |
| 16к |
| f, Гц |
| Δf/f, % Гц |
| N = 40 дБ |
| 50 дБ |
| 60 дБ |
| 80 дБ |
| Рис. 4. Зависимость минимально различимой слухом разницы по частоте Δf/f от частоты f звукового сигнала при различных значениях его уровня (40, 50, 60 и 80 дБ) |
Из рис. 4 видно, что в области низких частот – примерно до частоты 1 кГц, разрешающая способность слуха по частоте определяется почти одинаковым абсолютным значением изменения частоты тона, которое равно приблизительно 2-3 Гц, хотя в ряде случаев отмечалось значение всего в 1 Гц. В области более высоких частот (от 1 кГц и выше) отмечается постоянство относительного значения Δf/f, которое составляет здесь величину примерно равную 0,004 (дробь Вебера). Например, на частоте 5 кГц Δf = 20 Гц, на частоте 10 кГц Δf = 40 Гц и т.д.
Из рис. 4 также видно, что уменьшение уровня рассматриваемого тона приводит к увеличению дифференциальных частотных порогов, т.е. чем тише звук, тем труднее его отличить по частоте от других звуков.
| N, дБ |
| Δf,Гц |
| Рис. 5. Зависимость минимально различимой слухом девиации частотыΔfтонального звукового сигнала 1 кГц от его уровня N |
На рис. 5 показана зависимость порогового значения девиации частоты Δf от уровня N исследуемого звукового сигнала в качестве которого использован тональный сигнал с частотой 1 кГц. Очевидно, что для сигналов малой интенсивности (N< 30 дБ) пороговое значение Δf велико: чем слабее сигнал – тем хуже разрешающая способность слуха по частоте. Однако при увеличении уровня сигнала более 30 дБ пороговое значение девиации стабилизируется и в дальнейшем остается практически постоянным и равным примерно 2-3 Гц.
Временные дифференциальные пороги
Органы чувств человека, и слух в том числе, являются по своей природе инерционными. Даже для приблизительной оценки характера и меры ощущения требуется некоторое время. Для точной же количественной оценки того или иного параметра ощущения времени требуется гораздо больше. Кроме того, разные параметры требуют для точной оценки разного времени. Поэтому исследования разрешающей способности слуховой системы во временной области проводятся в нескольких направлениях.
1) Анализ минимального времени, в течение которого слух способен различить два сигнала. Исследования в данной области показали, что минимальный интервал времени между двумя следующими друг за другом тональными сигналами, необходимый для того чтобы слух распознал их именно как два сигнала, а не один, составляет около 2 мс. Оказалось, что эта величина почти не зависит ни от частоты тонального сигнала, ни от его интенсивности. Однако для определения какой из двух сигналов поступает первым, а какой вторым (если это сигналы двух разных частот), необходимо время порядка 20 мс. Для определения высоты тона в области низких частот требуется примерно 60 мс, в области высоких частот – примерно 15 мс.
2) Анализ дифференциальной чувствительности к изменению длительности звукового сигнала. Здесь в ходе эксперимента испытуемым предлагалась последовательность групп из двух сигналов каждая – один сигнал из каждой пары имел длительности Т мс, а другой несколько большую - (Т+ΔТ) мс. Сигналы подавались в случайном порядке и эксперт должен был определить, какой из двух сигналов в паре имеет большую длительность. Значения ΔТ при этом изменялись от одной пары к другой в случайном порядке. Наименьшую разницу, правильно определенную экспертами в 75% случаев, принимали за JND (дифференциальный порог) для длительности (ΔТ).
В результате эксперимента оказалось, что по мере уменьшения общей длительности Т воздействия сигнала ΔТ также начинает уменьшаться, т.е. чем короче сигналы, тем меньшую разницу между ними способен заметить человеческий слух. Например, при длительности Т сигнала вблизи 1 с пороговое значение ΔТ составляет примерно 50 мс, а при длительности Т сигнала 0,5 мс ΔТ также составляет 0,5 мс. Дифференциальная временная чувствительность ΔТ/Т (дробь Вебера) здесь константой не является, а изменяется вместе с изменением длительности Т таким образом, что при Т = 0,5-1 мс она равна 1, при Т = 10 мс - примерно 0,3 и при Т = 50-500 мс – приблизительно 0,1. Полученные результаты при этом почти не зависят ни от высоты, ни от интенсивности звукового сигнала.
3) Анализ чувствительности слуха к изменению времени установления (атаки) или спада звукового сигнала. Время установления и время спада звука являются чрезвычайно важными характеристиками звучания различных музыкальных инструментов, поскольку изменяя эти параметры, можно до неузнаваемости изменить тембр звучания инструмента. Исследования показали, что дифференциальный порог для времени установления (как и для времени спада) составляет: для частот ниже 1 кГц – 1 мс, для частот 1-10 кГц – 0,5 мс. Если изменения времени атаки и спада звукового сигнала меньше, то для слуха они оказываются незаметными. В реальных условиях эти пороги могут оказаться даже большими, поскольку каждая отдельно взятая нота, как правило, в той или иной степени маскируется одновременно исполняемыми соседними звуками.
4) Анализ дифференциальной слуховой чувствительности к фазовым искажениям. Долгое время считалось, что человеческий слух не способен ощущать текущие изменения фазовых соотношений между спектральными компонентами в сложных звуковых сигналах. В этом вопросе ученые всего мира полагались на авторитетное утверждение Германа фон Гельмгольца – немецкого физика, физиолога и психолога, сделанное им еще в середине XIX века. Однако уже в 70-х годах ХХ века, когда в исследованиях стали использовать компьютерную технику, выяснилось, что этот постулат не соответствует действительности. Изменения фазовых соотношений между спектральными составляющими сигнала способны очень существенно изменять его временную структуру, что, в свою очередь, выражается в изменении тембра звучания и четкости определения высоты музыкального сигнала. Выяснилось, что более всего слух чувствителен к скорости изменения фазы, т.е. к групповому времени задержки (ГВЗ):
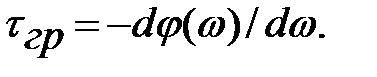
Установлено, что минимальный дифференциальный слуховой порог для искажений ГВЗ наблюдается на частоте 2 кГц и составляет ~ 1 мс (рис. 6).
Знание дифференциальных слуховых порогов важно для проектирования звуковоспроизводящей и акустической аппаратуры, поскольку позволяет устанавливать искажения ниже порогов заметности человеческим слухом.
Следует, однако, заметить, что полной ясности в проблеме установления порогов чувствительности слуха к изменению временной структуры звукового сигнала пока еще нет. Поэтому исследования этого вопроса с использованием современных компьютерных технологий продолжаются во многих научных учреждениях различных стран мира.
| f, кГц |
| 0,5 |
| t, мс |
| Рис. 6. Пороги слуховой чувствительности для ГВЗ |
Контрольные вопросы
1. Что такое относительная (дифференциальная) чувствительность?
2. Каким образом оценивают дифференциальные слуховые пороги, используя два сигнала?
3. Каким образом оценивают дифференциальные слуховые пороги, используя один сигнал?
4. Как зависит дифференциальная чувствительность слуха по частоте от частоты?
5. Как зависит дифференциальная чувствительность слуха по частоте от амплитуды?
Литература
1. В.А. Никамин. Зрительно-слуховое восприятие аудиовизуальных программ.: Учебник / ГОУВПО СПбГУТ. – СПб, 2014.
2. Акустика: Учебник для вузов / Ш.Я. Вахитов, Ю.А. Ковалгин, А.А. Фадеев, Ю.П. Щевьев; под ред. Ю.А. Ковалгина. – М.: Горячая линия-Телеком, 2009.
3. И.А. Алдошина, Р. Приттс. Музыкальная акустика. Учебник. – СПб.: Композитор. – СПб, 2006.
Порядок выполнения работы
Открыть программу AdobeAudition, щелкнув дважды по ее ярлыку.
1. Задать параметры звукового файла. Для этого:
- В меню Файл (File) щелкнуть Новый (New) и в открывшемся окне установить:
- Частоту дискретизации (SampleRate) – 48кГц;
- Каналы (Channels) – Моно;
- Разрешение (Resolution) – 32 бит.
Нажать кнопку ОК.
2. В меню Создать (Generate) щелкнуть Тоны (Tones) и в открывшемся окне (рис. 7) установить:
- Основнуючастоту (BaseFrequency) – f =1000 Гц;
- Форму сигнала (Flavor) – синус (Sine);
- Длительность(Duration) – 4 секунды.
- dB Громкость (dBVolume) – (–10…–20) дБ;
| Рис. 7. Окно установки параметров сигнала программы AdobeAudition |
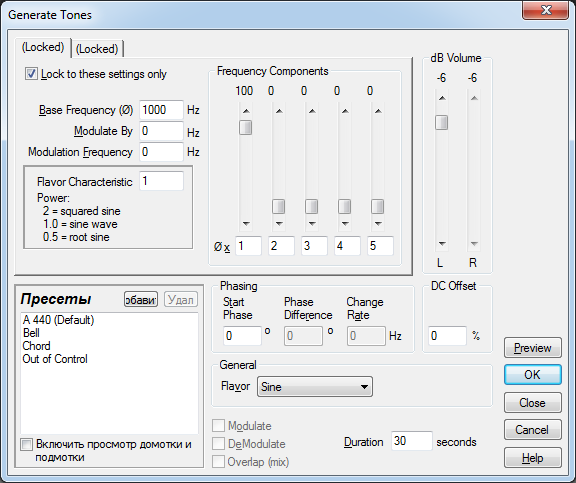
3. Нажать кнопку Preview и прослушать полученный сигнал. Перемещая ручку регулятора dB Громкость (dBVolume) найти такое ее положение, которое будет соответствовать порогу слышимости звукового сигнала на этой частоте. Для того чтобы облегчить дальнейшие вычисления, лучше поступить следующим образом. Установить ручку регулятора dB Громкость (dBVolume) в какое-либо фиксированное положение вблизи обнаруженного порога слышимости с круглым значением уровня громкости – например, – 70 дБ, и с помощью регулятора громкости телефонов или компьютера добиться, чтобы это значение соответствовало порогу слышимости, т.е. задать некоторую точку отсчета в 0 дБ (N0). Отметить это значение громкости N0в дБ в табл. 1.
4. В окне ModulationFrequencyустановить значение модулирующей частоты Ω = 4 Гц.
5. Установить уровень громкости звукового сигнала Nна 40 дБ больше относительно N0 с помощью регулятора dB Громкость (dBVolume). Если N0 = – 70 дБ, то N = – 30 дБ.
6. В окне ModulateByустановить значение девиации Δω = 1 Гц. Нажав кнопку Preview прослушать полученный сигнал. Если модуляция на слух не ощущается, то повторить п.5, увеличивая Δω = 2 Гц, 3 Гц и т.д., до тех пор, пока модуляция не будет слышна отчетливо. В соответствующую ячейку таблицы 1занестизначение Δf= 2Δω.
7. Повторить пп. 5 и 6 для N= 50 дБ и N= 60 дБ, занося полученные результаты в соответствующие ячейки таблиц 2 и 3.
8. Повторить пп. 2-7 для всех частот, указанных в таблицах 1-3.
9. Рассчитать значения Δf/f в % и занести их в соответствующие ячейки таблиц 1-3.
10. Построить графики зависимости Δf/f от частоты для разных уровней громкостиN
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ
Им. проф. М.А.Бонч-Бруевича
Кафедра РПВЭС и ЭА
Студент__________________ Группа__________
ОТЧЕТ
По лабораторной работе №2
по курсу
«Зрительно-слуховое восприятие аудиовизуальных программ»
«Исследование дифференциальных порогов слуха по частоте с помощью программы ADOBEAUDITION»
Табл. 1
Уровень звукового сигнала N= 40 дБ (N0 = -70 дБ)
| Частота, Гц | |||||||||||
| Δf, Гц | |||||||||||
| Δf/f, % |
Табл. 2
Уровень звукового сигнала N= 50 дБ (N0 = -70 дБ)
| Частота, Гц | |||||||||||
| Δf, Гц | |||||||||||
| Δf/f, % |
Табл. 3
Уровень звукового сигнала N= 60 дБ (N0 = -70 дБ)
| Частота, Гц | |||||||||||
| Δf, Гц | |||||||||||
| Δf/f, % |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAcjUtqMUA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQYvCMBSE78L+h/AWvGmquFKqUaQgK6IHXS97ezbP tti8dJuodX+9EQSPw8x8w0znranElRpXWlYw6EcgiDOrS84VHH6WvRiE88gaK8uk4E4O5rOPzhQT bW+8o+ve5yJA2CWooPC+TqR0WUEGXd/WxME72cagD7LJpW7wFuCmksMoGkuDJYeFAmtKC8rO+4tR sE6XW9wdhyb+r9LvzWlR/x1+v5TqfraLCQhPrX+HX+2VVjAajeF5JhwBOXsAAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQByNS2oxQAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA " filled="f" stroked="f" strokeweight=".5pt">
| 16 к |
| 1 к |
| 2 к |
| 4к |
| 8к |
| f, Гц |
| Δf/f, % |
| Графики зависимости минимально различимой на слух разницы по частотеΔf/f от частоты звукового сигнала f при различных значениях уровней громкости |
Выводы
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Работа выполнена «___»______________20___ г.
___________________________________________
(подпись преподавателя)
Отчет проверен «___»_________________20___ г.
___________________________________________
(подпись преподавателя)
