Нелинейные системы автоматического регулирования
Нелинейные системы автоматического регулирования
Нелинейными называются системы, движение которых описывается нелинейными дифференциальными уравнениями. Реальные САР всегда являются нелинейными. Дифференциальные уравнения могут быть нелинейными вследствие того, что в них «нелинейно» (т.е. не в 1-ой степени) входят некоторые координаты системы или их производные по времени, а также вследствие того, что коэффициенты уравнения являются линейными или нелинейными функциями координат или их производных.
Если нелинейность не велика, систему можно линеаризовать и применять при ее исследовании методы линейной теории.
Динамическая система «существенно нелинейная», если при помощи линейных моделей нельзя описать наиболее характерные черты происходящих в ней переходных и установившихся процессов.
Устойчивые линейные системы характеризуются следующими свойствами (особенностями):
1. Подчиняются принципу суперпозиции (принципу наложения) объединенного действия). Это означает, что если на вход линейного звена с передаточной функцией W (Р) подаются одновременно два сигнала, то реакция на выходе будет равна сумме реакций на каждый из этих сигналов.

1.  ;
;
2.  ;
;
3.  .
.
Пусть  ,
,
тогда  .
.
2. Устойчивость в «большом», т.е. устойчивость при любых по величине начальных отклонениях ее координат, физически возможных в данной системе.
3. Только одна форма движения — асимптотическое приближение к состоянию покоя (равновесия).
4. Изохронизм колебаний (период колебаний не зависит от их амплитуды).
5. Период вынужденных колебаний равен периоду действующей силы.
6. Амплитуда вынужденных колебаний пропорциональна амплитуде действующей силы,
7. Форма резонансной кривой, т.е. АЧХ, не зависит от амплитуды действующей силы.
Нелинейные системы не обладают перечисленными свойствами. При подаче на вход гармонического колебания, вынужденные колебания могут носить самую разнообразную форму, например:
1) они могут иметь другую частоту;

2) форма выходных колебаний может быть практически независимой от формы входных колебаний;

3) частота, а следовательно и форма резонансной кривой могут существенно изменяться при изменении амплитуды входных колебаний.
Из рассмотренных примеров следует, что принцип суперпозиции к нелинейным системам не применим. Нелинейная САР может быть при одних начальных условиях устойчивой, а при других нет. В нелинейных системах могут возникать автоколебания — периодическое движение, не зависящее от начальных условий, а возникающее вследствие динамических свойств самой системы.
В нелинейных системах содержится хотя бы одно нелинейное звено.
Типовые нелинейности
Рассмотрим типовые нелинейные элементы.
1. Идеальное реле


 ,
,
т.е. 
 .
.
2. Реле с зоной нечувствительности


3. Реле с зоной возврата


4. Реле с гистерезисом



5. Усилительное звено с зоной нечувствительности


6. Усилительное звено c ограниченной амплитудой выходной величины (с насыщением)


7. Усилительное звено с зоной нечувствительности и насыщением


8. Усилительное звено с зоной застоя




Типы нелинейных звеньев 1, 2, 5, 6 — являются однозначными, т.к. каждому значению входной величины соответствует вполне определенное значение выходной величины; звенья 3, 4, 8 — неоднозначные.
Пример нелинейной САР

1. Уравнение объекта
 ;
;
 .
.
2. Уравнение датчика (термопары с потенциометром)


X - передвижение движка реохорда
3. Уравнение нелинейного элемента



 .
.
U2 — напряжение питания реверсивного двигателя
4. Реверсивный двигатель — интегрирующее звено


Составим структурную схему

Ее можно представить:


Свойства фазовых траекторий
1. Фазовые траектории направлены по часовой стрелке, т.е. если производная положительна, то X увеличивается.

2. Фазовая траектория пересекает ось абсцисс под прямым углом. Т.к. в данном случае  , a
, a  , то
, то  .
.

Обозначим


тогда  .
.
В состоянии равновесия


 — угол наклона в данном случае неопределенный. Точки, соответствующие состоянию равновесия, называются особыми точками.
— угол наклона в данном случае неопределенный. Точки, соответствующие состоянию равновесия, называются особыми точками.
Сколько может быть состояний равновесия?
У линейных систем — одно, т.к. Р и Q — линейны, а две линии пересекаются в одной точке.

У нелинейных систем точек равновесия может быть несколько.

3. Через одну точку фазовой плоскости проходит только одна фазовая траектория (это утверждение основано на теореме Коши о единственности решения дифференциального уравнения).
Очень важным является суждение об устойчивости систем. Для линейных систем много критериев устойчивости. Когда выше мы говорили об устойчивости, то речь шла о единственном установившемся состоянии.
Для нелинейных систем существует несколько установившихся состояний (режимов), из которых некоторые устойчивые, некоторые неустойчивые. Здесь имеет смысл говорить лишь об устойчивости нелинейной системы в окрестности данного состояния равновесия.
Для нелинейных систем различают устойчивость: в малом, в большом, в целом.
Устойчивость в малом - это устойчивость при бесконечно малых отклонениях от исходного режима.
Устойчивость в большом — это устойчивость при конечных отклонениях, возможных в данной системе по условиям ее работы.
Устойчивость в целом — это устойчивость при неограниченных отклонениях.
Теорема Ляпунова
Если линейная система, соответствующая уравнению 1-ого приближения устойчива, то нелинейная система также устойчива в окрестности состояния равновесия.
Если линейная система неустойчива; то и нелинейная система неустойчива.
Если линейная система находится на границе устойчивости, то по уравнению 1-ого приближения нельзя судить об устойчивости состояния равновесия нелинейной системы.
Пример. Определить состояния равновесия и устойчивы ли они?
1)





1-ая точка равновесия: 
2-ая точка равновесия: 


 ;
;
для 
для 
Применим необходимое условие устойчивости: положительность всех коэффициентов дифференциального уравнения. Оно не выполняется. Следовательно, оба состояния равновесия неустойчивы.
Метод изоклин
Изоклиной называется геометрическое место точек, где касательные к фазовым траекториям имеют одинаковый наклон.
Запишем уравнение системы 2-ого порядка:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 — тангенс угла наклона фазовой траектории
— тангенс угла наклона фазовой траектории
Геометрическим местом точек, где тангенс угла наклона равен  , будет:
, будет:
 .
.

Линии OC1, OC2,…, OC8 — изоклины.
Если соединим строки, то получим фазовый портрет. Из любой начальной точки мы теперь можем перейти в следующую и т.д. Если начали в A0 и пришли в A0 — имеем цикл.
Пример.
 ;
;
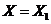 ;
;
 ;
;
 ;
;
 ;
;
 — уравнение изоклины
— уравнение изоклины





Нелинейные системы автоматического регулирования
Нелинейными называются системы, движение которых описывается нелинейными дифференциальными уравнениями. Реальные САР всегда являются нелинейными. Дифференциальные уравнения могут быть нелинейными вследствие того, что в них «нелинейно» (т.е. не в 1-ой степени) входят некоторые координаты системы или их производные по времени, а также вследствие того, что коэффициенты уравнения являются линейными или нелинейными функциями координат или их производных.
Если нелинейность не велика, систему можно линеаризовать и применять при ее исследовании методы линейной теории.
Динамическая система «существенно нелинейная», если при помощи линейных моделей нельзя описать наиболее характерные черты происходящих в ней переходных и установившихся процессов.
Устойчивые линейные системы характеризуются следующими свойствами (особенностями):
1. Подчиняются принципу суперпозиции (принципу наложения) объединенного действия). Это означает, что если на вход линейного звена с передаточной функцией W (Р) подаются одновременно два сигнала, то реакция на выходе будет равна сумме реакций на каждый из этих сигналов.

1.  ;
;
2.  ;
;
3.  .
.
Пусть  ,
,
тогда  .
.
2. Устойчивость в «большом», т.е. устойчивость при любых по величине начальных отклонениях ее координат, физически возможных в данной системе.
3. Только одна форма движения — асимптотическое приближение к состоянию покоя (равновесия).
4. Изохронизм колебаний (период колебаний не зависит от их амплитуды).
5. Период вынужденных колебаний равен периоду действующей силы.
6. Амплитуда вынужденных колебаний пропорциональна амплитуде действующей силы,
7. Форма резонансной кривой, т.е. АЧХ, не зависит от амплитуды действующей силы.
Нелинейные системы не обладают перечисленными свойствами. При подаче на вход гармонического колебания, вынужденные колебания могут носить самую разнообразную форму, например:
1) они могут иметь другую частоту;

2) форма выходных колебаний может быть практически независимой от формы входных колебаний;

3) частота, а следовательно и форма резонансной кривой могут существенно изменяться при изменении амплитуды входных колебаний.
Из рассмотренных примеров следует, что принцип суперпозиции к нелинейным системам не применим. Нелинейная САР может быть при одних начальных условиях устойчивой, а при других нет. В нелинейных системах могут возникать автоколебания — периодическое движение, не зависящее от начальных условий, а возникающее вследствие динамических свойств самой системы.
В нелинейных системах содержится хотя бы одно нелинейное звено.
Типовые нелинейности
Рассмотрим типовые нелинейные элементы.
1. Идеальное реле


 ,
,
т.е. 
 .
.
2. Реле с зоной нечувствительности


3. Реле с зоной возврата


4. Реле с гистерезисом



5. Усилительное звено с зоной нечувствительности


6. Усилительное звено c ограниченной амплитудой выходной величины (с насыщением)


7. Усилительное звено с зоной нечувствительности и насыщением


8. Усилительное звено с зоной застоя




Типы нелинейных звеньев 1, 2, 5, 6 — являются однозначными, т.к. каждому значению входной величины соответствует вполне определенное значение выходной величины; звенья 3, 4, 8 — неоднозначные.
Пример нелинейной САР

1. Уравнение объекта
 ;
;
 .
.
2. Уравнение датчика (термопары с потенциометром)


X - передвижение движка реохорда
3. Уравнение нелинейного элемента



 .
.
U2 — напряжение питания реверсивного двигателя
4. Реверсивный двигатель — интегрирующее звено


Составим структурную схему

Ее можно представить:


