Оценка точности неравноточных измерений одной и той же величины.

Формулы и обозначения.

L_i - результат измерений

Р_i - вес результата измерений

L=[P_l]/ [P] - вероятнейшее значение измеренной величины(3.29)

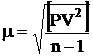- средняя квадратическая ошибка единицы веса (3.30)

m_L = μ / Ö Р - средняя квадратическая ошибка вероятнейшего

значения (3.31)

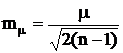
- средняя квадратическая ошибка величины (3.32)

μ (надежность оценки)

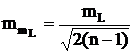- средняя квадратическая ошибка величины (3.33)

m_L (надежность оценки)

v_i = L – l_i - вероятнейшая поправка (3.34)

Р_v = w [P] - контроль вычислений значений L и v (3.35)

w = L_окр. – L_точн. - ошибка округления значения L (3.36)

Вопросы для программированного контроля знаний студентов.

По первому разделу:

1.Какой принцип разграфки и обозначения листов карты масштабов: 1:1000000,1:500000,1:300000,1:200000,1:100000,

1:50000,1:25000,1:10000,1:5000?

2.Какие размеры рамок листов карты в градусной величине для масштабов 1:1000000 - 1:5000?

3.Как вычислить номер шестиградусной зоны по номеру колонны в международной разграфке и наоборот?

4.Как определить где находится точка относительно осевого меридиана, если известно её ордината?

5.Как определить в какой шестиградусной зоне находится точка, если известна её ордината?

6.Что принимается за оси абсцисс и ординат в проекции Гаусса?

7.Что искажается в проекции Гаусса (углы, линии, площади)?

8.Как вычисляются прямоугольные координаты в проекции Гаусса для углов рамок листов карт в масштабах 1:25000 и 1:10000?

По второму разделу:

1.Как определить геодезические координаты (широту и долготу) точки, указанной на карте?

2.Как определить прямоугольные координаты (х, у) точки, заданной на карте?

3.Как вычислить для отрезка линии, заданной на карте, уклон и угол наклона?

4.Как вычислить дирекционный угол и горизонтальное проложение отрезка линии, заданного на карте, определив графические координаты его концов?

5.Как определить магнитный азимут линии, если известны румб, среднее сближение меридианов и склонение магнитной стрелки?

6.Как найти дирекционный угол линии, если известны магнитный румб, среднее сближение меридианов и склонение магнитной стрелки?

По третьему разделу:

1.По каким формулам производится оценка точности, то есть вычисляется средняя квадратическая ошибка (С.К.О.):

-одного измерения по истинным ошибкам;

- одного измерения по вероятнейшим поправкам;

- одного измерения и среднего из двух измерений по разностям двойных равноточных измерений;

- функции измеренных величин общего вида;

- линий функций;

- вероятнейшего значения (арифметической средины и весовой арифметической средины) измеряемой величины;

- единицы веса;

- определения самой величины С.К.О.(надёжность оценки точности).

2.По каким формулам вычисляется вес или обратный вес:

- измерения с известной С.К.О.;

- функции измеренных величин (общего вида);

- линейной функции;

-арифметической средины и весовой арифметической средины.

3.Какой порядок математической обработки результатов равноточных и неравноточных измерений одной и той же величины?

4.Как вычисляется С.К.О. и предельная ошибка суммы измеренных величин, если известны их С.К.О.?

5.Как найти вес суммы измеренных величин, если известны весы этих величин?

Приложение А.

Таблица соответствия № ряда букве латинского алфавита.

Nр	Буква	Nр	Буква	Nр	Буква
	A		I		R
	B		J		S
	C		K		T
	D		L		U
	E		M		V
	F		O		Z
	G		P
	H		Q

Рекомендуемая литература:

1. Маслов А. В., Гордеев А. В., Батраков Ю. Г. Геодезия. М.: Недра, 1993.

2. Неумывакин Ю. К., Смирнов А.С. Практикум по геодезии. М. Картгеоцентр-Геодезиздат,1995.

3. Таблицы Гауса-Крюгера.

4. Условные знаки.

Содержание

	Введение
	Общие указания
	Порядок и методика расчетов при выполнении курсовой работы.
	Вопросы для программированного контроля и защиты курсовой работы.