Тема №26 «Анализ и сглаживание временных рядов»

Цель:научиться находить основные характеристики временного ряда, сглаживать ряд методами наименьших квадратов и скользящего среднего, проверять значимость уравнения тренда, делать краткосрочный и среднесрочный прогнозы.

Краткие теоретические сведения:

Под временным рядом (динамическим рядом, или рядом динамики) подразумевается последовательность наблюдений некоторого признака (случайной величины) Х в последующие равноотстоящие моменты времени.

Отдельные наблюдения называются уровнями ряда - 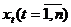, 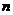– число уровней.

В общем виде при исследовании временного ряда 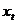выделяется несколько составляющих: 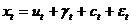( 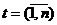, где:

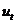– тренд, плавно меняющаяся компонента, описывающая тенденцию изменения признака,

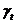– сезонная компонента, отражающая повторяемость процессов в течение не очень длительного периода,

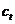– циклическая компонента, отражающая повторяемость процесса в течение длительных периодов,

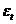– случайная компонента, отражающая влияние неподдающихся учету и регистрации случайных факторов.

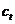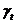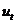, , – являются закономерными, неслучайными.

Стационарные временные ряды – ряды, вероятностные свойства которых не изменяются во времени.

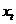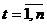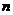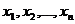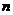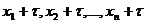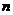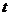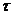Временной ряд ( ) называется строго стационарным, если совместное распределение вероятностей наблюдений такое же, как и наблюдений при любых , и , то есть закон распределения и его числовые характеристики не зависят от времени. Следовательно, среднее значение и дисперсия может быть оценены по наблюдениям 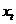( 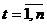) по формулам:

,

.

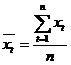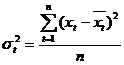Степень тесноты связи между наблюдениями временного ряда 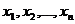и 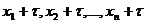(сдвинутых относительно друг друга на 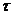единиц) может быть определена с помощью автокорреляционной функции .

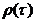Статистической оценкой 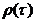является выборочный коэффициент автокорреляции :

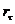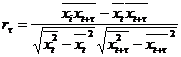
Функцию 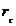называют выборочной автокорреляционной функцией, а её график – коррелограммой. При расчете 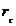обычно берут .

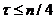Важнейшей классической задачей при исследовании временных рядов является выявление и статистическая оценка основной тенденции (тренда) развития изучаемого процесса и отклонений от неё, а также прогнозирование на его основе дальнейшего развития процесса.

Для выявления основной тенденции чаще всего используется метод наименьших квадратов.

Другим методом выравнивания временного ряда, то есть выделения неслучайной составляющей является метод скользящих средних. Он основан на переходе от начальных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. Получаемый таким образом ряд скользящих средних ведет себя более гладко, чем исходный ряд, из-за усреднения отклонений ряда.

Значимость полученного уравнения тренда проверяется по 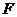- критерию. Затем можно приступать к прогнозу.

Если рассматривать временной ряд как регрессионную модель изучаемого признака по переменной «время», то к нему применимы рассмотренные выше методы анализа.

Следует, однако, иметь в виду, что при работе с временными рядами возмущения во многих случаях не являются независимыми случайными величинами с математическим ожиданием равным нулю. Если последовательные значения 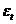коррелируют между собой, то говорят об автокорреляции возмущений.

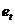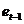С помощью критерия Дарбина – Уотсона проверяется гипотеза об отсутствии автокорреляции между соседними остаточными членами ряда и , где 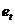– выборочная оценка .

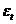Статистика имеет вид: .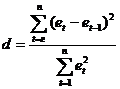

При достаточно большом : .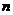

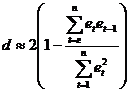Если 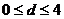: 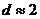– корреляция отсутствует, 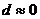– полная положительная корреляция, 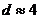– полная отрицательная корреляция.

Если 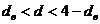– гипотеза об отсутствии автокорреляции принимается, 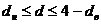или 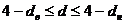– в таком случае вопрос остается открытым, 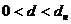– принимается альтернативная гипотеза о положительной автокорреляции, 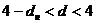– принимается альтернативная гипотеза об отрицательной автокорреляци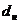и.

и 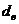находим в таблице критических точек Дарбина – Уотсона.

В случае отсутствия автокорреляции возмущений методом регрессионного анализа может быть найдена не только точечная, но и интервальная оценка уровней ряда, то есть осуществлены их точечный и интервальный прогнозы.

Если в рассматриваемой регрессионной модели автокорреляция возмущений существует, то необходимы меры по её устранению. Используются различные методы.

Один из них - использование авторегрессионной модели, в которых регрессорами выступают лаговые переменные, то есть переменные влияние которых в регрессионной модели характеризуется некоторым запаздыванием.

Авторегрессионная модель 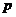-го порядка:

, ( ).

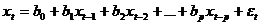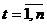Контрольные вопросы:

1. Временной ряд, его уровни.

2. Составляющие временного ряда.

3. Основная задача исследования временных рядов.

4. Основные этапы анализа временных рядов.

5. Стационарные и строго стационарные временные ряды.

6. Автокорреляционная функция и её оценка.

7. Методы сглаживания временного ряда.

8. Проверка значимости уравнения тренда.

9. Автокорреляция возмущений.

10. Критерий Дарбина – Уотсона.

11. Методы снижения автокорреляции возмущений.

12. Точечный и интервальный прогнозы развития изучаемого процесса.

13. Авторегрессионная модель.

Контрольные задания:

В таблице приведены данные, отражающие цену и спрос на некоторый лекарственный препарат за восьмилетний период (усл. ед.):

Год,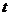
Цена,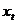
Спрос,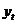

а) для ряда 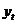найти среднее значение, СКО и коэффициенты автокорреляции (для лагов 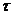=1;2),

б) для временного ряда 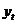найти уравнение тренда, полагая его линейным,

в) проверить значимость полученного уравнения по 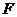- критерию на 5%-ном уровне значимости,

г) провести сглаживание временного ряда 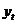методом скользящих средних, используя простую среднюю арифметическую с интервалом сглаживания 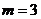года,

д) выявить на уровне значимости 0,05 наличие автокорреляции возмущений для временного ряда ,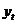

е) дать точечную и интервальную оценки прогноза среднего и индивидуального значений спроса на девятый год,

ж) выяснить на уровне значимости 0,05, оказывает ли цена влияние на спрос.

З) для ряда 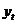составить авторегрессионную модель, проверить её значимость по 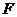- критерию на 5%-ном уровне значимости.

Задания для домашней работы:

Провести анализ ряда 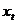из предыдущего задания.

Самостоятельная работа