Тема №15 «Применение непараметрических критериев»

Цель:научиться применять критерий 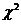- Пирсона, 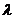- критерий Колмогорова, 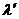- критерий Колмогорова – Смирнова, ранговый критерий Уилкоксона для сравнения эмпирического распределения с теоретическим или для установления однородности двух эмпирических распределений.

Краткие теоретические сведения:

Если закон распределения генеральной совокупности неизвестен, то соответствующие критерии, используемые для установления этого закона, называются непараметрическими.

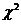- критерий Пирсона:

Критерий согласия Пирсона служит для проверки гипотезы о предполагаемом законе распределения. Сравнивается эмпирическое распределение с теоретическим, но возможно и сравнение двух эмпирических распределений.

1) выдвигаем гипотезу о том, что данное эмпирическое распределение подчиняется конкретному закону,

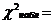
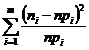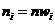2) находим , где и 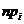- эмпирические и теоретические частоты,

то есть определяем меру расхождения эмпирических и теоретических частот,

3) для выбранного уровня значимости по таблице 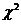- распределения находим критическую точку 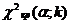, где 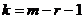, 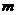- число интервалов эмпирического распределения, 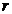- число параметров теоретического распределения,

4) если 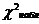< 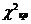, то частоты расходятся незначительно, а, следовательно, нет оснований отвергать нулевую гипотезу.

Критерий Колмогорова:

Имеет то же назначение что и критерий Пирсона.

1) выдвигаем гипотезу о том, что данное эмпирическое распределение подчиняется конкретному закону,

2) строим эмпирическую функцию распределения 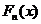и предполагаемую теоретическую ,

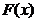3) находим 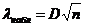, где ,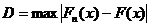

4) по таблице критических точек для данного уровня значимости находим ,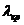

5) если 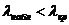, то принимаем нулевую гипотезу.

Критерий Колмогорова – Смирнова:

Служит для проверки гипотез об однородности выборки – то есть гипотез о том, что рассматриваемые выборки извлечены из одной о той же генеральной совокупности. Сравниваются две эмпирические функции распределения.

1) выдвигаем гипотезу о том, что выборки однородны,

2) находим 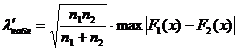, где 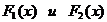- эмпирические функции распределения, построенные по двум выборкам объемов 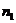и ,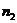

3) при 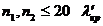находим в специальных таблицах, при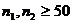 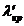совпадает со статистикой Колмогорова ,

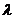4) если 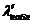< 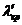, то принимаем нулевую гипотезу, то есть выборки однородны.

Ранговый критерий Уилкоксона:

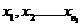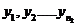Критерий Уилкоксона служит для проверки однородности двух независимых выборок: и , распределения которых неизвестны, но величины должны быть непрерывными. Если выборки однородны, то считают, что они извлечены из одной и той же генеральной совокупности и, следовательно, имеют одинаковые, причем неизвестные, непрерывные функции распределения 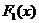и .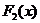

1) выдвигаем нулевую гипотезу о том, что выборки однородны, то есть 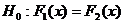, тогда конкурирующая гипотеза ( ), [ ],

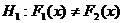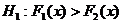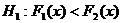2) ранжируем варианты обеих выборок, 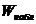- сумма рангов номеров вариант первой выборки,

3) 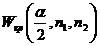( 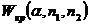), [ 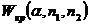] находим по таблице критических точек Уилкоксона, если ,

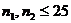и 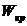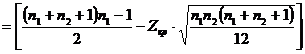, где [ ] – целая часть числа, 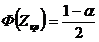( 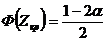), [ 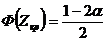] находим, используя таблицу функции Лапласа, если ,

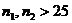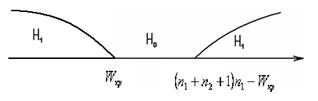
4) находим ещё одну критическую точку по формуле ,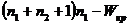

5) если ( > ), [ < ].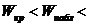

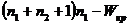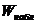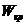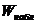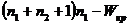Контрольные вопросы:

1. Назначение 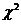- критерия Пирсона.

2. Наблюдаемое и критическое значения критерия Пирсона.

3. Алгоритм сравнения эмпирического распределения с теоретическим с помощью критерия Пирсона.

4. Назначение 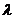- критерия Колмогорова.

5. Наблюдаемое и критическое значения критерия Колмогорова.

6. Алгоритм сравнения эмпирического распределения с теоретическим с помощью критерия Колмогорова.

7. Назначение 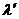- критерия Колмогорова – Смирнова.

8. Наблюдаемое и критическое значения критерия Колмогорова - Смирнова.

9. Алгоритм сравнения двух эмпирических распределений с помощью критерия Колмогорова.

10. Ранговый критерий Уилкоксона.

11. Правила ранжирования.

12. Наблюдаемое и критическое значения критерия Уилкоксона.

13. Алгоритм проверки однородности двух выборок с помощью критерия Уилкоксона.

Контрольные задания:

1. Вычислить, исходя из гипотезы о нормальном распределении генеральной совокупности, теоретические частоты и, используя критерий Пирсона, при уровне значимости 0,05 установить, случайно или значимо расхождение между эмпирическими частотами 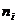и вычисленными теоретическими .

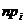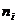2. В гениальной комедии Н. В Гоголя «Женитьба» у купеческой дочери Агафьи Тихоновны было четыре жениха. На смотринах внимательная тётушка наблюдала за поведением Агафьи:

благосклонно смотрела на Никанора Ивановича 14 раз

благосклонно смотрела на Ивана Кузьмича 5 раз

благосклонно смотрела на Ивана Павловича 8 раз

благосклонно смотрела на Бальтазара Бальтазарыча 5 раз

Кому из женихов Агафья Тихоновна отдаёт наибольшее предпочтение?

3. В выборке из здоровых лиц мужского пола, студентов технических и военно-технических вузов в возрасте от 19 до 22 лет, средний возраст 20 лет, проводился тест Люшера в 8 -цветном варианте. Установлено, что жёлтый цвет предпочитается испытуемыми чаще, чем отвергается. Можно ли утверждать, что распределение жёлтого цвета по 8 позициям у здоровых испытуемых отличается от равномерного распределения? Экспериментальные данные наблюдаемых частот попадания жёлтого цвета на каждую из восьми позиций представлены в таблице.

Позиции жёлтого цвета
Наблюдаемые частоты

4. Сопоставить данные, полученные в предыдущем примере, с данными обследования

Х. Кларом 800 испытуемых. Х. Кларом было показано, что жёлтый цвет является единственным цветом, распределение которого по восьми позициям не отличается от равномерного. Для сопоставления им использовался метод 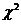. Полученные им наблюдаемые частоты представлены в таблице.

Позиции жёлтого цвета
Наблюдаемые частоты

5. При уровне значимости 0,05 проверить нулевую гипотезу об однородности двух выборок объёмов 6 и 8 при конкурирующей гипотезе .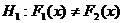

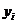6. При уровне значимости 0,01 проверить нулевую гипотезу об однородности двух выборок объёмов 30 и 50 при конкурирующей гипотезе 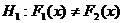, если известно, что в общем вариационном ряду, составленном из вариант обеих выборок, сумма порядковых номеров вариант первой выборки 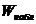=1600.

Задания для домашней работы:

1. Используя критерий Пирсона, при уровне значимости 0,05 установить, случайно или значимо расхождение между эмпирическими частотами 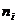и теоретическими 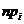, которые вычислены исходя из гипотезы о нормальном распределении генеральной совокупности

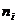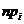2. В эксперименте психологу необходимо использовать шестигранный игральный кубик с цифрами на гранях от 1 до 6. Для чистоты эксперимента необходимо получить «идеальный» кубик, то есть такой, чтобы при достаточно большом числе подбрасываний каждая его грань выпадала бы примерно равное число раз. Задача состоит в выяснении того, будет ли данный кубик близок к идеальному? Для решения этой задачи психолог подбрасывал кубик 60 раз, при этом количество выпадений каждой грани распределилось следующим образом:

Грани кубика
Количество выпадений

3. Известны результаты психологического тестирования в виде двух выборок, объёмы которых соответственно равны 6. При уровне значимости 0,05 проверить нулевую гипотезу об однородности при конкурирующей гипотезе .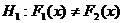

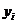4. Используя критерий Уилкоксона, при уровне значимости 0,05 проверить нулевую гипотезу об однородности двух выборок, объёмы которых соответственно равны 30 и 50, при конкурирующей гипотезе 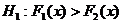, если известно, что сумма порядковых номеров вариант первой выборки в общем вариационном ряду 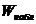=1150.