Тема №4 «Вычисление вероятностей случайных событий»

Цель: усвоить основные понятия теории вероятностей – достоверные, невозможные, случайные события; совместные и несовместные события; научиться использовать классическое, статистическое и геометрическое определения вероятности.

Краткие теоретические сведения:

Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.

Опытом (испытанием) называется всякое осуществление определённого комплекса условий или действий, при которых наблюдается соответствующее явление.

Событием называется всякий возможный факт, который в результате опыта может произойти или не произойти. Обозначаются большими латинскими буквами.

Достоверным называют событие, которое обязательно произойдет в данном опыте.

Невозможным Ø называют событие, которое в данном опыте не может произойти.

Случайным называют событие, которое в данном опыте может произойти, но может и не произойти.

Два события A и B называются несовместными, если в данном испытании они не могут произойти вместе.

Два события A и B называются совместными в данном испытании, если появление одного из них не исключает возможность появления другого события в этом же испытании.

Несколько событий образуют полную группу, если они несовместны и единственно возможные исходы испытания.

Если в полной группе только два события, то они называются противоположными.

Исход опыта называется благоприятствующим некоторому событию, если его появление влечет за собой появление данного события.

Вероятность некоторого события есть числовая мера объективной возможности наступления этого события.

Вероятностью события называется отношение числа благоприятствующих исходов к общему числу исходов (классическое определение вероятности): .

Пример. Урна содержит 5 белых и 7 черных шаров, тщательно перемешанных. Какова вероятность того, что взятый наудачу из урны один шар окажется белым?

Решение. В данном испытании имеется всего 12 возможных исходов, из них 5 благоприятствуют появлению белого шара. Поэтому вероятность появления белого шара .

Относительной частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведённых опытов: .

Пример. Монетку подбросили 100 раз. Герб появился 52 раза. Тогда вероятность появления герба .

Вероятностью события называется число, около которого группируются значения относительной частоты (статистическое определение вероятности).

Геометрической вероятностью события А называется отношение меры области, благоприятствующей событию А, к мере всей области: .

Пример. Найти вероятность попадания точки в круг, вписанный в квадрат со стороной .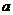

Решение. Площадь круга, вписанного в квадрат со стороной 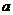, равна - мера области, благоприятствующей нашему событию, площадь квадрата - - мера всей области. Тогда искомая вероятность равна .

Свойства вероятности:

1) ,

2) Ø ,

3) .

Контрольные вопросы:

1. Испытание, событие. Достоверное и невозможное события. Совместные и несовместные события. Равносильные, равновозможные и единственно возможные события. Полная группа событий. Противоположные события. Элементарные исходы. Благоприятствующие исходы.

2. Классическое определение вероятности.

3. Относительная частота события. Статистическое определение вероятности. Свойство устойчивости относительной частоты.

4. Отличие классического и статистического определений вероятности.

5. Мера области. Геометрическое определение вероятности.

6. Размещения с повторениями, размещения без повторений, перестановки, сочетания.

7. Свойства вероятностей событий.

Контрольные задания:

1. Подбрасывается игральная кость, какова вероятность выпадения 5-ти очков.

2. В коробке 3 белых и 2 чёрных шара. Найти вероятность выбора белого шара из коробки.

3. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.

4. В колоде 36 игральных карт. Наудачу выбирают одну карту. Найти вероятность, что она окажется:

а) тузом,

б) красной,

в) пиковой дамой,

г) не картинкой.

5. Слово составлено из карточек, на каждой из которых написана одна буква. Карточки смешивают и вынимают без возврата по одной. Найти вероятность того, что буквы вынимаются в порядке слова МАТЕМАТИКА.

6. В коробке 12 деталей, 8 из них нестандартные. Наудачу извлечены 3 детали. Найти вероятность того, что среди них окажется только 2 стандартные детали.

7. Из колоды вынимают 3 карты. Найти вероятность того, что:

а) среди них окажется два туза,

б) хотя бы один туз.

8. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлекают 10 карточек. Найти вероятность того, что среди них окажется нужная.

9. Наудачу выбирается четырёхзначное число. Найти вероятность того, что в десятичной записи этого числа нет нуля.

10 Колода из 36 карт разделена на две равные части. Найти вероятность того, что в каждой части будет по два туза.

11. Найти вероятность угадать шестизначный телефонный номер.

12. Найти вероятность угадать шестизначный телефонный номер, зная, что цифры в нём не повторяются.

13. Внутрь круга радиуса R брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг:

а) квадрата,

б) правильного треугольника.

14. Территория нефтебазы имеет форму прямоугольника со сторонами 50 и 30 метров. На территории имеется 4 круглых нефтебака диаметром 10 метров каждый. Какова вероятность поражения нефтебака бомбой, попавшей на территорию нефтебазы.

Задания для домашней работы:

1. В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины.

2. Из 5 букв разрезной азбуки составлено слово «книга». Ребенок, не умеющий читать, рассыпал эти буквы и затем собрал их в произвольном порядке. Найти вероятность того, что у него получится слово «книга».

3. В мешочке содержится 10 одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному 3 кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3, если кубики извлекаются:

а) без возврата,

б) с возвратом.

4. Студент успел подготовить 20 вопросов из 25. Какова вероятность того, что из трёх выбранных вопросов студент знает не менее двух.

5. Два парохода должны подойти к одному и тому же причалу. Время прихода независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придётся ждать освобождения причала, если время стоянки первого парохода 2 часа, а второго - 3 часа.