Тема №2 «Элементы математической логики»

Цель: научиться приводить дизъюнктивные и конъюнктивные нормальные формы к совершенным дизъюнктивным и конъюнктивным нормальным формам, используя логические равносильности; применять законы математической логики для решения логических задач; применять язык логики предикатов для записи математических предложений, определений, построения противоположных утверждений.

Краткие теоретические сведения:

Высказывание – любое повествовательное предложение, которому можно приписать истинностное значение.

Предложение, которое содержит хотя бы одну переменную и становится высказыванием при подстановке вместо всех переменных их значений, называется высказывательной формой.

Высказывание, представляющее собой одно утверждение, называется элементарным.

Высказывание, образованное из элементарных с помощью логических связок «и», «или», «если, то», «не», называется составным (сложным).

Образование составного высказывания из элементарных называется логической операцией.

Логическая операция, соответствующая логической связке «не» («неверно, что») называется отрицанием: . Отрицание истинно, когда основное высказывание ложно.

Логическая операция, соответствующая логической связке «и», называется конъюнкцией: . Конъюнкция истинна, когда истинны оба высказывания.

Логическая операция, соответствующая логической связке «или», называется дизъюнкцией: . Дизъюнкция ложна, когда ложны оба высказывания.

Логическая операция, имеющая вид «если , то », называется импликацией: . Высказывание называется посылкой, – заключением. Импликация ложна, когда посылка истинна, а заключение ложно.

Логическая операция, соответствующая сложному союзу «тогда и только тогда, когда», называется эквиваленцией: . Эквиваленция истинна, когда оба высказывания одновременно истинны или одновременно ложны.

Приоритет логических операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.

Под формулой 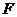логики высказываний понимается следующее:

1) всякое элементарное высказывание есть формула,

2) если и – формулы, то , , , , ,

3) других формул, кроме перечисленных в 1) и 2), нет.

Две формулы называются равносильными, если их таблицы истинности совпадают: .

Основные формулы математической логики:

1) - закон тождества,

2) - закон противоречия,

3) - закон исключённого третьего,

4) - снятие двойного отрицания,

5) , - идемпотентность,

6) , - коммутативность,

7) , - ассоциативность,

8) , - дистрибутивность,

9) , - законы Де Моргана,

10) , , , - сочленение переменной с константой,

11) , - законы поглощения,

12) , - законы склеивания,

13) , - замена импликации,

14) - правило modus ponens,

15) - правило силлогизма,

16) - закон контрапозиции,

17) - соединение посылок,

18) - разъединение посылок.

Примеры. 1) Доказать формулу .

Решение.

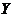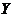Видим, что средний столбик состоит из одних единиц, равносильность доказана.

2) Упростить формулу .

Решение.

.

Формула называется тождественно – истинной (тавтологией) (тождественно – ложной (противоречием)), если её истинностное значение «истина» («ложь») при любых возможных значениях переменных.

Предложение называется прямым утверждением, - обратным, - противоположным, - обратнопротивоположным.

Если предложение - истинно, то оно называется теоремой. - достаточное условие для 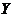, 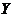- необходимое условие для или следствие .

Если - истинно и - истинно, то 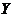- необходимое и достаточное условие для , а - необходимое и достаточное условие для .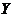

Дизъюнктивная нормальная форма (ДНФ) представляет собой дизъюнкцию конъюнкций переменных и их отрицаний, либо конъюнкцию самих переменных.

Конъюнктивная нормальная форма (КНФ) представляет собой конъюнкцию дизъюнкций переменных и их отрицаний, либо дизъюнкцию самих переменных.

Любую формулу можно привести к ДНФ или к КНФ.

Совершенная дизъюнктивная нормальная форма(СДНФ) – дизъюнкция конъюнкций, содержащих все исходные переменные (с отрицанием или без).

Совершенная конъюнктивная нормальная форма(СКНФ) – конъюнкция дизъюнкций, содержащих все исходные переменные (с отрицанием или без).

Пример. Привести к ДНФ формулу .

Решение.

.

Функция, все значения которой принадлежат множеству {0; 1} называется предикатом: , .

Предикат с 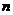различными переменными называется 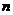– местным предикатом.

Подмножество области определения предиката, состоящее из тех и только тех элементов, которым соответствует истинное значение предиката, называется областью истинности предиката.

Если область истинности предиката совпадает со всей областью определения, то предикат называется тождественно – истинным. Если же область истинности представляет собой пустое множество, то предикат называется тождественно – ложным.

Всякий одноместный предикат с переменной 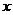, принимающей значения из некоторого непустого множества, выражает свойство, присущее некоторым элементам этого множества. Множество элементов, обладающих свойством , называется объёмом данного свойства. Многоместные предикаты выражают отношения.

Кванторы:

1) - квантор всеобщности,

2) - квантор существования,

3) - квантор существования единственности.

Контрольные вопросы:

1. Высказывание. Простые и составные высказывания. Высказывательная форма.

2. Операции алгебры логики: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция и их свойства.

3. Формула алгебры логики. Равносильные формулы алгебры логики. Тавтология. Противоречие.

4. Основные равносильности.

5. Виды теорем. Необходимое и достаточное условия.

6. Элементарная конъюнкция. Дизъюнктивная нормальная форма (ДНФ). Совершенная дизъюнктивная нормальная форма (СДНФ).

7. Элементарная дизъюнкция. Конъюнктивная нормальная форма (КНФ). Совершенная конъюнктивная нормальная форма (СКНФ).

8. Предикат. Область истинности предиката.

Контрольные задания:

1. Доказать тождественную истинность основных формул математической логики.

2. Упростить:

а) ,

б) ,

в) (( → )→ )→ ,

г) ( → ) ( → ) ( ).

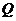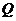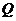3. Привести формулу 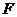к СДНФ и СКНФ, предварительно приведя её равносильными преобразованиями к ДНФ и КНФ:

4. Решить задачу:

По подозрению в совершённом преступлении задержали Брауна, Джона и Смита. Один из них был уважаемым в городе стариком, другой был малоизвестным чиновником, третий – известным мошенником. В процессе следствия старик говорил правду, мошенник лгал, а третий задержанный в одном случае говорил правду, а в другом – ложь. Вот что они утверждали:

Браун: «Я совершил это. Джон не виноват»,

Джон: «Браун не виноват. Преступление совершил Смит»,

Смит: «Я не виноват, виноват Браун».

Определить имя старика, мошенника и чиновника и кто из них виноват, если известно, что преступник один.

5. Найти область истинности предиката : «быть кратным трём», если:

а) область определения {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15},

б) {3,6,9,12,15},

в) {1,2,5,7,11,14}.

6. Записать на языке логики предикатов определения:

а) периодической функции,

б) чётной функции,

в) построить отрицания определений в примерах а) и б).

Задания для домашней работы:

1. Доказать равносильность следующих формул: и .

2. Решить задачу:

Известно, что если Джонс не встречал ночью Смита, то Смит – убийца. Джонс говорит неправду или Смит не убийца. Джонс говорит правду. Верно ли, что Джонс встретил ночью Смита.

3. Найти область истинности предиката : «х³-5х²+6х>0» и .