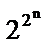Булевы функции. Законы алгебры логики. Аналитические способы описания. Полные системы функций

Цель работы:изучение способов описания булевых функций, практическое применение законов алгебры логики, представление функций в различных базисах.

Теоретическая справка

Определение функции алгебры логики

Пусть множество Х состоит из двух элементов 0 и 1, Х={0,1}; множество Y=Xⁿ = {(x₁, …,x_n) | "i = , x_i Î X}.

Двоичный набор –совокупность координат некоторого фиксированного вектора (х₁, …, х_n) Î Хⁿ.

Каждому двоичному набору можно поставить в соответствие некоторый номер, равный двоичному числу соответствующему данному набору.

Пусть (х₁, х₂, …, х_n) – логический набор, тогда х₁*2^n-1+х₂*2^n-2+…+x_n*2⁰ – номер набора.

Например:

(0,1,1) = 0×2² + 1×2¹+1×2⁰ = 3

(0,0,1,1) = 0×2³+0×2² +1×2¹+1×2⁰ = 3

Замечание. Чтобы восстановить набор по номеру – нужно знать количество аргументов.

Логическая переменная – это переменная, которая может принимать только два значения: истина или ложь (TRUE/FALSE, 1/0).

Функция алгебры логики (булева функция, ФАЛ) – f(x₁,x₂, …,x_n) – это функция, у которой все аргументы есть логические переменные, и сама функция принимает только логические значения.

	Количество всевозможных, различных двоичных наборов длиной n равно 2n.

Например:

Построим всевозможные двоичные наборы длиной n = 3.

По теореме, приведенной выше, их количество равно 2ⁿ = 2³ = 8.

Номер двоичного набора	Двоичный набор
х1	х2	х3

Существуют следующие способы описания ФАЛ

- табличный

- графический

- аналитический

- словесный

Табличный способ представления ФАЛ

Любую булеву функцию можно представить таблицей, имеющей 2ⁿ строк. Такая таблица называется таблицей истинности.

В левой части таблицы перечисляются всевозможные двоичные наборы значений аргументов, а в правой части – значения некоторой булевой функции.

№	x1	х2	…	хn	f (х1, х2,…,хn)
			…		a1
			…		a2
…	…	…	…	…	…
2n-1			…		a2n

	Число различных ФАЛ, зависящих от n аргументов конечно и равно

Графическое представление ФАЛ

ФАЛ можно представить в виде n-мерного единичного куба: если наборам значений аргументов сопоставить точки n-мерного пространства, то множество 2ⁿ наборов определяет множество вершин n-мерного куба.

Одномерный куб (n = 1)

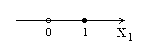Функция принимает значения либо 0, либо 1.

F=0 – пустой кружёчек,

F=1 – закрашенный кружёчек.

Двумерный куб (n = 2)

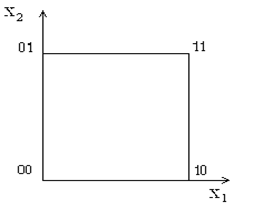
Трехмерный куб (n = 3)

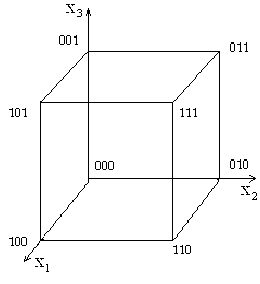
Таким же способом можно задать функцию от четырех переменных, в виде четырехмерного куба.

Четырехмерный куб (n = 4)

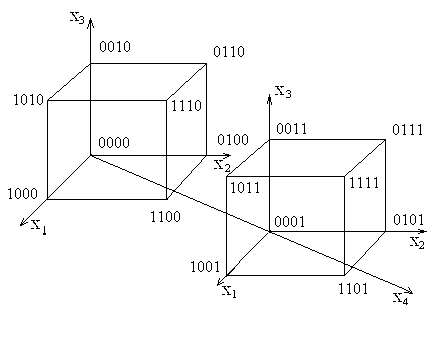Функции алгебры логики одного аргумента

Количество функций от одного аргумента равно 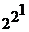= 4.

Функции алгебры логики одного аргумента

х	f0(x)	f1(x)	f2(x)	f3(x)

f₀(х) º 0 – константа 0 («ложь»)

f₁(х) º 1 – константа 1 («истина»)

f₂(х) = х – переменная х

f₃(х) = 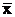- отрицание х (инверсия х)

Функции алгебры логики двух аргументов

Количество различных ФАЛ от двух аргументов равно 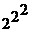= 16.