Основные законы алгебры множеств
1) Коммутативные законы
А È В = В È А
А Ç В = В Ç А
А D В = В D А
2) Ассоциативные законы
А È (В È С) = (А È В) È С
А Ç (В Ç С) = (А Ç В) Ç С
3)Дистрибутивные законы
А È (В Ç С) = (А È В) Ç (А È С)
А Ç (В È С) = (А Ç В) È (А Ç С)
4) Законы с Æ и U
А È Æ = А А Ç U = А А È 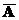 = U
= U
А Ç Æ = Æ А È U = U А Ç 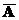 = Æ
= Æ
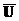 = Æ
= Æ 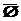 = U
= U
6) Законы идемпотентности
А Ç А = А А È А = А 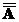 = А
= А
7) Законы поглощения
А È (А Ç В) = А
А È ( 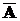 Ç В) = А È В
Ç В) = А È В
А Ç (А È В) = А
А Ç ( 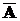 È В) = А Ç В
È В) = А Ç В
8) Законы де Моргана
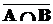 =
= 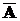 È
È 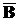
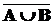 =
= 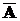 Ç
Ç 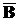
9) Законы склеивания
(А Ç В) È ( 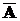 Ç В) = В
Ç В) = В
(А È В) Ç ( 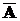 È В) = В
È В) = В
Справедливость законов алгебры множеств доказывается на основе определения равенства: Х = Y, если
1)Х Í Y:" x Î X Þ x Î Y;
2) YÍ Х:" y Î Y Þ y Î X.
Сформулированный принцип называют интуитивным принципом объемности.
Задание к лабораторной работе.
Заданы множества X, Y, Z, U.
Правило образования множеств X, Y, Zи U:
X - множество букв имени студента;
Y - множество букв отчества студента;
Z - множество букв фамилии студента;
U - универсальное множество = X È Y È Z È{ъ,ё, гласные, отсутствующие в множествах X, Y, Z}.
1.Вычислить:
- X Ç Y , X Ç Z, Y ÇZ, X Ç Y Ç Z;
- Y È Z , X È Y È Z;
- X \ Z, Z \ X;
- X È 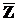 ;
;
- X D Z ;
- X Ç 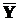 , X È (Y Ç Z);
, X È (Y Ç Z);
- (X \ Z) È (Y \ Z).
2. Нарисовать диаграммы Эйлера для:
- X Ç Y Ç Z;
- (X Ç Y) È 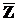 ;
;
- ( 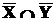 Ç
Ç 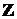 );
);
-(X \ Z) È (Y \ Z).
3. Проверить экспериментально на множествах X, Y, Z справедливость следующих утверждений:
- 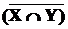 =
= 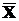 È
È 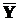 ;
;
- 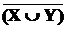 =
= 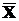 Ç
Ç 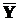 ;
;
- X \ (Y È Z) = (X \ Y) Ç (X \ Z);
- X \ (Y Ç Z) = (X \ Y) È (X \ Z).
4. Записать булеан для произвольного подмножества множества Zмощности 4.Выписать все возможные разбиения и привести примеры 3 покрытий этого подмножества.
Контрольные вопросы.
1. Дать определение множества.
2. Привести примеры конечных и бесконечных множеств.
3. Указать существующие способы задания множеств.
4. Дать определения пустого и универсального множеств.
5. Что называют подмножеством множества?
6. Ввести понятия операций над множествами.
7. Привести примеры операций над множествами с помощью кругов Эйлера.
8. Записать основные законы и теоремы алгебры множеств.
Лабораторная работа № 2
Отношения на множествах
Цель работы:изучение способов задания отношений, приобретение практических навыков в проверке основных свойств отношений, классификация отношений.
Теоретическая справка
Прямое (декартово) произведение множеств Х и Y – множество упорядоченных пар, таких что:
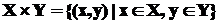 .
.
При X = Y множество 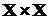 называется декартовой степеньюмножества Xи обозначается X2.
называется декартовой степеньюмножества Xи обозначается X2.
Бинарное отношение на множествах X и Y – произвольное подмножество прямого произведения двух множеств 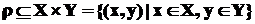 .
.
Если r Í Х2, то отношение r задано на множестве Х.
Если (x,y)Îr,то (x,y) находятся в отношении rили связаны отношением r: х r yили y = r(х) .
Область определения Drбинарного отношения - множество первых элементов каждой упорядоченной пары Dr = {x | (x,y) Î r}.
Область значений Jr бинарного отношения - множество вторых элементов каждой упорядоченной пары
J r = {y | (x, y) Î r}.
Способы задания отношений
1) Список пар
r = {(1,5), (2,4), (3,6), (6,2)} на r Í Х2, Х= {1,2,3,4,5,6}
2) Характеристическая функция
r = {(n,m)| n = 2*m}
3) Графическое изображение
 r ={(1,5), (2,4), (3,6), (6,2)} на r Í Х2, Х= {1,2,3,4,5,6}
r ={(1,5), (2,4), (3,6), (6,2)} на r Í Х2, Х= {1,2,3,4,5,6}
4) Матрица отношения
r ={(1,5), (2,4), (3,6), (6,2)} на r Í Х2, Х= {1,2,3,4,5,6}
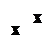
 | ||||||||
| ||||||||
Свойства бинарных отношений
Пусть rзадано на множестве X, r Í Х2
Рефлексивность: " х Î Х х r х .
Антирефлексивность: 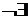 х Î Х х r х.
х Î Х х r х.
Нерефлексивность: $ х Î Х (x, x) Ï r.
Симметричность: " х, y Î Х х r y => y r х.
Антисимметричность: " х, y Î Х х r y, y r х Û x = y.
Транзитивность: " х, y, z Î Х х r y, y r z => x r z.
Отношение порядка – антисимметрично, транзитивно.
Отношение нестрого порядка ( 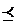 ) - рефлексивно,
) - рефлексивно,
антисимметрично,
транзитивно.
Отношение строгого порядка ( 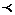 ) - антирефлексивно,
) - антирефлексивно,
антисимметрично,
транзитивно.
В отношениях полного порядка все элементы сравнимы между собой, а в отношениях частичного порядка не все элементы сравнимы между собой.
Отношение эквивалентности ( ~ )- рефлексивно,
симметрично,
транзитивно.
Класс эквивалентности для х : [ x ] = { yÎ Х | x ~ y}.
Обратное отношение получается путём перестановки значений в парах исходного отношения.
Композиция отношений r иg -отношение, состоящее из пар
r○g={(x, z)| х r у, y g z }
Например:
Отношения r и g заданы на множестве Х = {1, 2, 3, 4, 5, 6,}.
r= {(1,4), (2,5), (3,6), (4,1), (6,3)},
g = {(1,1), (2,3), (3,4), (4,5), (5,6), (6,6)}.
Область определения Dr= {1, 2, 3, 4, 6}.
Область значений J r= {1, 3, 4, 5, 6}.
Обратное отношение r-1={(4,1), (5,2), (6,3), (1,4), (3,6)}.
Отношение r- антирефлексивно, не симметрично, не транзитивно.
Область определения Dg= {1, 2, 3, 4, 5, 6}.
Область значений J g= {1, 3, 4, 5, 6}.
Отношение g- не рефлексивно, антисимметрично, не транзитивно.
Композиция r ○ g={(1,5), (2,6), (3,6), (4,1), (6,4)}.
Например:
Отношение r= { (x, y) | сравнение по модулю m, x,y Î N }.
Отношение сравнения по модулю m на множестве натуральных чисел:x = y mod m, что означает x и y имеют одинаковый остаток при делении на m (классы вычетов по модулю m).
Отрезок натурального ряда N4={1,2,3,4}.
Отношение сравнения по модулю 2 на N4 :
d = { (1,1),(1,3),(2,2),(2,4),(3,1),(3,3),(4,2) ,(4,4)}.
Область определения Dd = {1, 2, 3, 4}.
Область значений J d = {1, 2, 3, 4}.
Отношение d - рефлексивно, симметрично, транзитивно.
Отношение d - отношение эквивалентности.
Классы эквивалентности: [ 1 ]={ 1,3 }=[ 3 ]
[ 2 ]={ 2,4 }=[ 4 ].
Например:
Отношения j и n заданы на множестве N4 .
j ={ (1,2), (2,3), (1,3), (3,4), (2,4), (1,4) }
n={ (1,1),(2,2),(3,3),(4,4) }.
Область определения Dj = { 1, 2, 3 }.
Область значений J j = { 2, 3, 4 }.
Отношение j - антирефлексивно, антисимметрично, транзитивно.
Отношение j - отношение строгого порядка.
Область определения Dn = { 1, 2, 3 ,4 }.
Область значений J n = { 1, 2, 3, 4 }.
Отношение n - рефлексивно, симметрично, антисимметрично, транзитивно.
Отношение n - отношение нестрогого частичного порядка.
Отношение n - отношение эквивалентности.
Классы эквивалентности: [ 1 ]={ 1}
[ 2 ]={ 2 }
[ 3 ]={ 3 }
[ 4 ]={ 4 }.
Функциональные отношения
Пусть r Í Хх Y.
Функциональное отношение– бинарное отношение r,для которого
" х Î Dr $ ! y Î Y: х r y.
Всюду определённое отношение– бинарное отношение r, для которого Dr =Х("нет одиноких х").
Сюръективное отношение – бинарное отношение r, для которого Jr = Y("нет одиноких y").
Инъективное отношение – бинарное отношение, в котором разным хсоответствуют разные у.
Биекция– функциональное, всюду определённое, инъективное, сюръективное отношение, задаёт взаимно однозначное соответствие множеств.
Например:
 Пусть r = { (x, y) Î R2 | y2 + x2 = 1, y > 0 }.
Пусть r = { (x, y) Î R2 | y2 + x2 = 1, y > 0 }.
Отношение r - функционально,
не всюду определено ("есть одинокие х"),
не инъективно (есть разные х,которым соответствуют одинаковые у),
не сюръективно ("есть одинокие у"),
не биекция.
Например:
Пусть Ã= {(x,y) Î R2 | y = x+1}
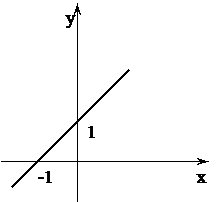
 Отношение Ã- функционально,
Отношение Ã- функционально,
Отношение Ã- всюду определено ("нет одиноких х"),
Отношение Ã- инъективно (нет разных х,которым соответствуют одинаковые у),
Отношение Ã- сюръективно ("нет одиноких у"),
Отношение Ã- биективно, взаимно-однородное соответствие.
Например:
Пусть j={(1,2), (2,3), (1,3), (3,4), (2,4), (1,4)} задано на множестве N4.
Отношение j - не функционально, x=1 соответствует три y: (1,2), (1,3), (1,4)
Отношение j - не всюду определенно Dj={1,2,3}¹ N4
Отношение j - не сюръективно Ij={1,2,3}¹ N4
Отношение j - не инъективно, разным x соответствуют одинаковые y, например (2,3) и (1,3).
Задание к лабораторной работе
1. Заданы множества N1 и N2. Вычислить множества:
(N1хN2) Ç (N2хN1);
(N1хN2) È (N2хN1);
(N1 Ç N2)x(N1 Ç N2);
(N1 È N2)x(N1 È N2),
где N1 = {цифры номера зачетной книжки, три последние};
N2 = {цифры даты и номера месяца рождения}.
2. Отношения rиgзаданы на множествеN6={1,2,3,4,5,6}.
Описать отношения r,g,r-1, r ○g, r-1 ○gсписком пар.
Найти матрицы отношений rиg.
Для каждого отношения определить область определения и область значений.
Определить свойства отношений.
Выделить отношения эквивалентности и построить классы эквивалентности.
Выделить отношения порядка и классифицировать их.
1) r= {(m,n) | m > n }
g= {(m,n) | сравнение по модулю 2}
2) r= {(m,n) | (m - n)делится на 2}
g= {(m,n) | mделитель n }
3) r= {(m,n) | m < n }
g= {(m,n) | сравнение по модулю 3}
4) r= {(m,n) | (m + n)- четно}
g= {(m,n) | m2=n }
5) r= {(m,n) | m / n -степень 2 }
g= {(m,n) | m = n }
6) r= {(m,n) | m / n -четно}
g = {(m,n) | m³n }
7) r= {(m,n) | m / n -нечетно }
g= {(m,n) | сравнение по модулю 4}
8) r= {(m,n) | m * n -четно }
g= {(m,n) | m£n }
9) r= {(m,n) | сравнение по модулю 5}
g= {(m,n) | mделится наn }
10) r= {(m,n) | m- четно, n - четно}
g= {(m,n) | mделительn }
11) r= {(m,n) | m = n }
g= {(m,n) | (m + n)£5 }
12) r={(m,n) | mи n имеют одинаковый остаток от деления на 3}
g= {(m,n) | (m-n)³2}
13) r= {(m,n) | (m + n) делится нацело на 2 }
g = {(m,n) | 2 £(m-n)£4}
14) r= {(m,n) | (m + n) делится нацело на 3 }
g= {(m,n) | m¹n }
15) r= {(m,n) | mи nимеют общий делитель }
g= {(m,n) | m 2£n }
16) r= {(m,n) | (m - n) делится нацело на 2 }
g= {(m,n) | m < n +2 }
17) r= {(m,n) | сравнение по модулю 4 }
g= {(m,n) | m£n }
18) r= {(m,n) | mделится нацело наn }
g= {(m,n) | m¹n , m- четно}
19) r= {(m,n) | сравнение по модулю 3 }
g= {(m,n) | 1 £(m-n)£3}
20) r= {(m,n) | (m - n) делится нацело на 4 }
g= {(m,n) | m¹n }
21) r= {(m,n) | m- нечетно, n - нечетно}
g= {(m,n) | m£n , n-четно}
22) r= {(m,n) | m и n имеют нечетный остаток от деления на 3 }
g= {(m,n) | (m-n)³1}
23) r= {(m,n) | m * n -нечетно }
g= {(m,n) | сравнение по модулю 2}
24) r= {(m,n) | m * n -четно }
g= {(m,n) | 1 £(m-n)£3}
25) r= {(m,n) | (m+ n) - четно}
g= {(m,n) | m не делится нацело на n }
26) r= {(m,n) | m = n }
g= {(m,n) | m делится нацело на n }
27) r= {(m,n) | (m - n )-четно}
g= {(m,n) | m делитель n }
28) r= {(m,n) | (m-n)³2}
g= {(m,n) | m делится нацело на n }
29) r= {(m,n) | m 2 ³ n }
g= {(m,n) | m / n -нечетно}
30) r= {(m,n) | m³n, m -четно}
g= {(m,n) | m и nимеют общий делитель, отличный от 1}
3. Определить является ли заданное отношение f -функциональным, всюду определенным, инъективным, сюръективным, биекцией (R- множество вещественных чисел). Построить график отношения, определить область определения и область значений.
Выполнить это же задание для отношений rи g из пункта 3 лабораторной работы.
1) f={ (x, y) Î R2 | y=1/x +7x }
2) f={ (x, y) Î R2 | x³y }
3) f={ (x, y) Î R2 | y³x }
4) f={ (x, y) Î R2 | y³x, x³ 0 }
5) f={ (x, y) Î R2 | y2 + x2 = 1 }
6) f={ (x, y) Î R2 | 2| y | + | x | = 1 }
7) f={ (x, y) Î R2 | x + y£ 1 }
8) f={ (x, y) Î R2 | x = y2 }
9) f={ (x, y) Î R2 | y = x3 + 1}
10) f={ (x, y) Î R2 | y = -x2 }
11) f={ (x, y) Î R2 | | y | + | x | = 1 }
12) f={ (x, y) Î R2 | x = y -2 }
13) f={ (x, y) Î R2 | y2 + x2 ³1, y> 0 }
14) f={ (x, y) Î R2 | y2 + x2 = 1, x> 0 }
15) f={ (x, y) Î R2 | y2 + x2£ 1, x> 0 }
16) f={ (x, y) Î R2 | x = y2 ,x³ 0 }
17) f={ (x, y) Î R2 | y = sin(3x + p) }
18) f={ (x, y) Î R2 | y = 1 /cos x }
19) f={ (x, y) Î R2 | y = 2| x | + 3 }
20) f={ (x, y) Î R2 | y = | 2x + 1| }
21) f={ (x, y) Î R2 | y = 3x }
22) f={ (x, y) Î R2 | y = e-x }
23) f ={ (x, y)Î R2 | y = e| x | }
24) f={ (x, y) Î R2 | y = cos(3x) - 2 }
25) f={ (x, y) Î R2 | y = 3x2 - 2 }
26) f={ (x, y) Î R2 | y = 1 / (x + 2) }
27) f={ (x, y) Î R2 | y = ln(2x) - 2 }
28) f={ (x, y) Î R2 | y = | 4x -1| + 2 }
29) f={ (x, y) Î R2 | y = 1 / (x2+2x-5)}
30) f={ (x, y) Î R2 | x = y3, y³ - 2 }.
Контрольные вопросы
1.Декартово или прямое произведение множеств.
2.Определение бинарного отношения.
3.Способы описания бинарных отношений.
4.Область определения и область значений.
5.Свойства бинарных отношений.
6.Отношение эквивалентности и классы эквивалентности.
7.Отношения порядка: строгого и нестрого, полного и частичного.
8.Классы вычетов по модулю m.
9.Функциональные отношения.
10. Инъекция, сюръекция, биекция.
Лабораторная работа № 3
