Установившееся течение несжимаемой жидкости в трубе. Гидродинамика.
Рассмотрим течение трубы за пределами входного участка.
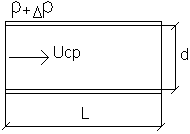
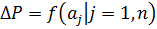
ΔP зависит от таких параметров:
- геометрические: L, d;
- кинематические: Uср;
- физическая жидкость: ρ, μ.
Тогда зависимость принимает вид:
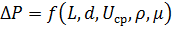
Из физических соображений ΔP~L,тогда зависимость принимает следующий вид:
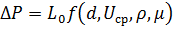
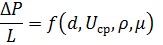
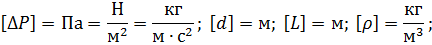
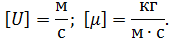
Не сложно проверить, что в данной задаче n=4, k=3.
В качестве базы выберем ρ, Uср, d.
Искомая зависимость будет иметь следующий вид:

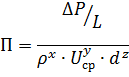
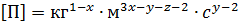
Для того, чтобы П было безразмерным показателем степени должны равняться нулю.
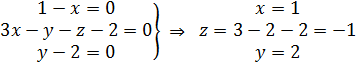
Определим вид величины
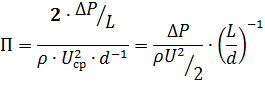
Найдем выражение для переменной П1:
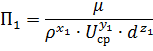
Определим x1 y1 z1 из условий безразмерности переменной П1.

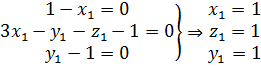
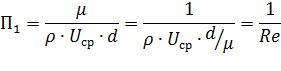
Подставим выражение П1 в исходную зависимость:
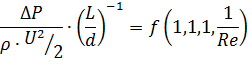
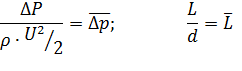
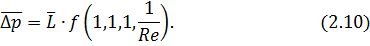

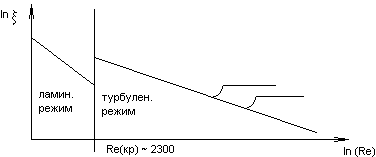
Если мы находимся в ламинарной зоне (слоистое течение), то инерционные свойства жидкости при установившемся течении на его картину не влияют.
В окончательной форме для случая ламинарного течения, (ρ) плотности быть недолжно.
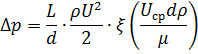
Если при: 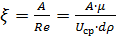 ;
;

Выражение Δр от ρ не зависит.

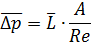
Теплообмен при течении в горизонтальной трубе.
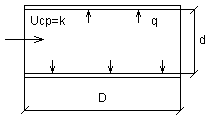
Любая задача теплообмена сводится к закону Ньютона-Райтмана.
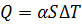
α – коэффициент теплоотдачи,
S – площадь поверхности,
ΔТ – разность температуры стенки.
Ищем коэффициент теплоотдачи α, а не тепловой поток.
Параметры:
- геометрические: L, d;
- кинематические: U, ρ, μ;
- тепловые (энергетические): Ср, α, λ.
Искомая зависимость будет иметь следующий вид:

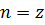
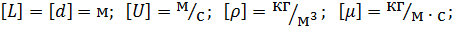
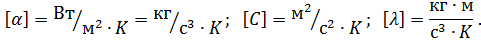

Выбираем базовые величины (d, U, ρ, λ).
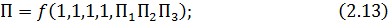
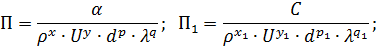
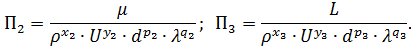
Определим показатели степени из размерности параметров Пi. Поскольку вид знаменателей во всех случаях Пi отличается индексом, то получим выражение для знаменателя.
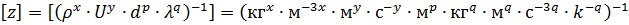
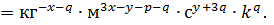
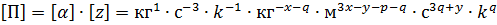
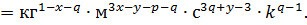
Для безразмерности [П] показатели должны быть равны нулю.
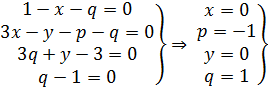
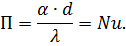
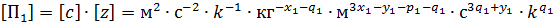
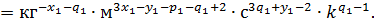
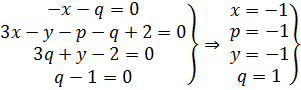
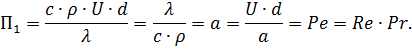
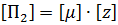 аналогично критерию П1 получим:
аналогично критерию П1 получим:
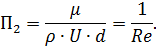
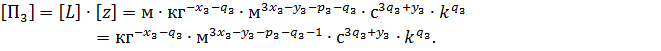
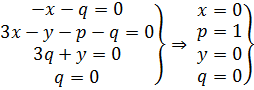
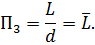
Выражение (2.13) принимает следующий вид:


Построение математической модели на основе законов сохранения
Общая форма законов сохранения.
Основной способ получения дифференциальных моделей – использование законов сохранения.
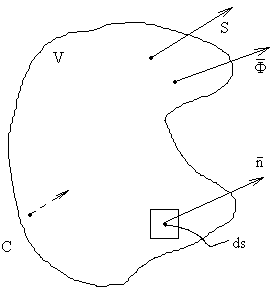
Законы сохранения – уравнение баланса исследуемой величины в некотором (конечном или бесконечно малом) объеме некоторого пространства. Выражаются законы сохранения следующим образом: изменение некоторой величины φ внутри некоторого объема V будет равно потоку величины Ф через границу s и порождению (исчезновению) источнику (стоку) величины φ внутри контрольного объема. 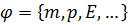
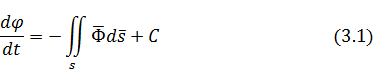

С – мощность внутренних источников величины φ;
Ф – поток φ через поверхность S;
n – единичная нормаль к поверхности S.
После подстановки получаем:

Закон сохранения величины φ – эмпирическое соотношение, оно не следует не из каких других соотношений подтверждено многократными опытами.
Примеры применения.
