Размерные и безразмерные величины.

Параметры процессов нуждаются в количественной оценке.

Размерность– масштаб для измерения величин.

Размерные величины – те, которые зависят от выбора масштаба.

Безразмерные величины – не зависят от системы единиц (кпд).

Если физические величины связаны некоторой зависимостью, то ей же и подчиняются и их размерности. В противном случае в формуле появятся дополнительные коэффициенты.

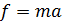
1)

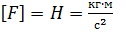
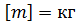
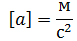
2) Путь будет введена независимая единица Н.

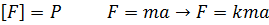
Сейчас используется основная система единиц СИ:

2.3. π – теорема.

Размерность любой произвольной единицы будет выражаться в виде одночлена размерности базовых величин.

[a] = L_c^α t^β M^γ T^æ (2.1)

[ρ] = M¹ L^-3 = кг/м³

[υ] = L t^-1 = м/с

Любое физическое соотношение между (n-1) размерными величинами может быть представлено в виде соотношения между [(n+1)-k] безразмерными величинами, где k ≤ n – число величин с независимыми размерностями.

Пусть зависимость имеет вид:

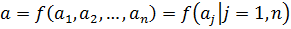(2.2)

Пусть первое k из 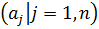были базовыми для данной задачи. Очевидно, что они должны быть независимыми (никакую из них нельзя выразить через остальные (k-1) базовых величин.

Например.

· Длина, плотность, скорость.

[L] = м, [ρ] = кг/м³, [u] = м/с.

М = [ρ ∙ r ∙ u]^β = кг^α ∙ м^-3α ∙ m^β ∙ c^-β – нет решений.

L – независима от [u] и [β], т.е. L, ρ, u – независимы.

· Длина, кинематическая вязкость, скорость.

[L] = м, [ν] = м²/с, [u] = м/с.

[L] = [ν]^α [u]^β ó C⁰ M¹ = M^2α C^-α M^β C^-β = M^2α+β-α-β

- α - β = 0

2α + β = 1

α = 1,

β = -1.

Т.е. L, ν, u – зависимы (их нельзя выбирать, как базовые).

· Длина, динамическая вязкость, скорость.

[L] = м, [μ] = кг/м∙с, [u] = м/с.

[L] = [μ]^α = [u]^β ó М¹ КГ⁰ С⁰ = КГ^α М^-α С^-α, М^β С^-β = КГ^α М^(β-α) С^(-α-β)

α = 0

β - α = 1

- α - β = 0

Система не имеет решений. Величины независимы.

Тогда остальные величины можно выразить через базовые j, i – индексы.

Поменяем масштабы для базовых величин в β_j раз, тогда их размерности в новой системе единиц [γ_j] = β_j [a_j], j = 1,k.

Для остальных величин (производных):

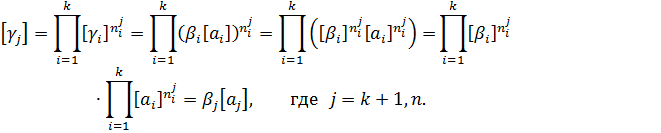
Например. Переход к новым системам единиц:

[L] = м, [t] = мин. U = 600 м/мин.

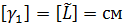
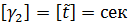
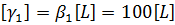
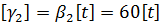
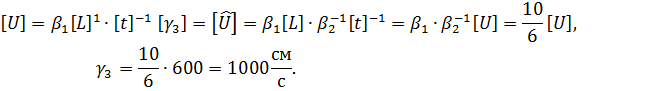
Данный пример даёт методику перехода к новой системе единиц измерения. В новой системе единиц измерения зависимость (2.2) принимает следующий вид:

,

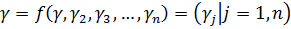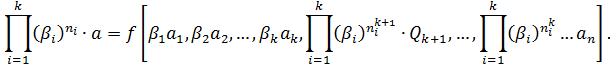
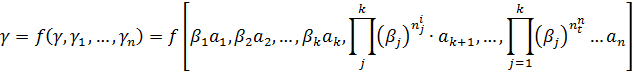
(2.4)

Поскольку, для независимых переменных можем масштаб 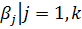выбирать произвольно, тогда выбираем их так, что первые k переменные зависимости «исчезли», т.е. чтобы .

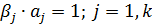Очевидно, что это достигается следующим образом: 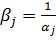(2.5)

Тогда остальные величины, с зависимыми размерностями следующие будут определяться следующими безразмерными величинами:

(2.6)

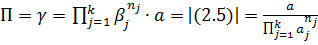
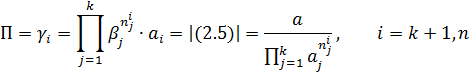
После подстановок результатов (2.6) в (2.4) вместо зависимости (2.2) мы получим:

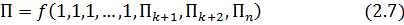
Зависимость (2.6) показатели степеней в знаменателе 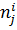ищутся из условий безразмерности новых переменных П_i.

Конец доказательства π-теоремы.

Следствие. Если n=k, то π-теорема позволяет определить вид функциональной зависимости (2.2) с точностью до производной постоянной. Для n=k выражение (2.7) принимает вид:

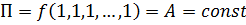
С учетом (2.6)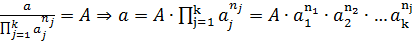

Замечание. 1) Осторожно! Искусственное занижение n приведет к неправильным результатам.

2)Теория размерностей не дает вид функциональных зависимостей (за исключением случаев n=k).

3)Основное положение теорий размерности, клонирование эксперимента и определение условий подобия моделируемых явлений реальными.

Примеры применения.