Дуальная классификация математической модели.

1. Структурные и функциональные модели.

Структурные – отражают структуру и связи между элементами (ПГС, ПЖРДУ).

Функциональные модели – отражают процесс моделируемого устройства (ф-ла тяги).

Структурные модели:

- топологические (схемы, графы);

- геометрические (чертежи).

Функциональные модели:

- имитационные («черный ящик» без описания сути процесса, обычно это полуэмпирические, эмпирические зависимости);

- аналитические (выражаются формулами из процесса описания внутри моделируемого объекта);

- детерминистские (без случайных величин);

- стохастические (со случайными величинами).

2. Теоретические и эмпирические модели.

Теоретические модели - следуют из аналитического исследования процессов внутри.

Эмпирические - следуют из обобщения экспериментального исследования.

Полуэмпирические модели – объединение обоих подходов (пример с дроссельной характеристикой).

Построение дроссельной характеристики по результатам эксперимента.

Полуэмпирическая модель

Эмпирические модели

Экспериментальные точки

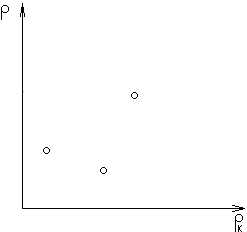
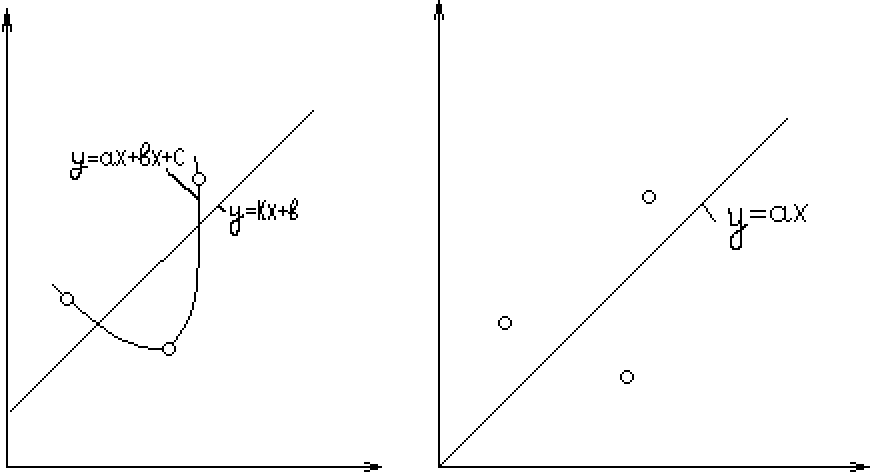
Используемые факты: P_k=0=>P=0 P~P_k

Стационарные и нестационарные модели:

a) Нестационарные параметры явно зависят от времени.

b) Стационарные от времени не зависят.

стационарные

нестационарные

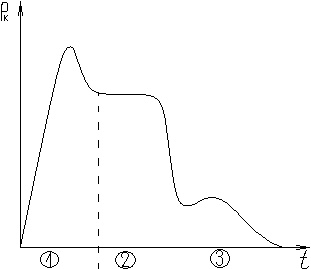
Подбором системы координат нестационарную задачу можно свести к стационарной задаче (торцевое горение твердого топлива).

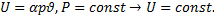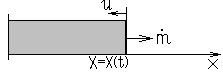
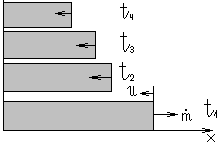
Зафиксируем систему координат на поверхности горения.

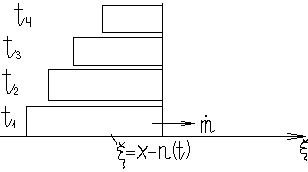
Линейные и нелинейные модели:

a) Линейные модели – это те, которые допускают суперпозицию воздействий и их пропорциональность.

,

;

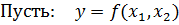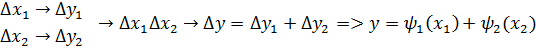
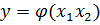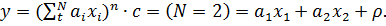
Иногда преобразованием параметров модель можно преобразовать в линейную модель.

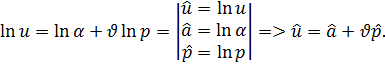
Если параметры процесса меняются незначительно, то модель можно линеаризовать.

Полагая: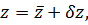

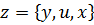
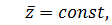
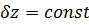
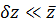
Классическое уравнение этой модели – это уравнение акустики.

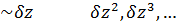
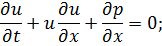
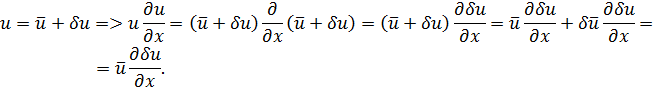
Непрерывные и дискретные модели:

b) Непрерывные модели – те, которые допускают малое изменение входных, выходных параметров.

c) Дискретные – допускают только скачкообразное изменение параметров.

Возможен переход при моделировании из одного класса в другой.

Кинетические уравнения для ф-ции распределения

Моделирование движения газа при увеличении плотности. С начала при малой плотности имеем:

Движение молекул

H

Уравнение Навъе-Стокса

КРС

H

D

D

Пространственная размерность модели.

Модели бывают: 0, 1, 2, 3-х мерные модели.

Реализация 2-х мерных моделей обыкновенные дифференциальные уравнения.

Реализация размерных уравнения частных производных.

Физическое моделирование и теория подобия

Моделирование и подобие.

Основной метод проектирования ракетной техники – экспериментальная отработка, поскольку, уравнения описывающие процессы в РД:

o неточны;

o не поддаются аналитическому решению.

Проведение экспериментальных исследований натурных образцов очень сложно, а зачастую невозможно => испытание нужно проводить в модельных условиях.

Основная задача физического моделирования – сформулировать условия, при которых возможен перенос результатов модельных испытаний на натурные образцы.

Базой для этого является понятие подобия.

Два (процесса, явления, объекта и т.п.) считаются подобными, если параметры одного из них получаются простым умножением параметрам другого на некий постоянный коэффициент, называемый критерием, ибо числом подобия.

, где

a1

a2

b2

b1

Можно выделить: - геометрические;

- кинематические;

- силовые;

- энергетическое подобие.

Таким образом, чтобы получить решение задач физического моделирования необходимо проводить его с равенством соответствующих чисел подобия.

Критерий подобия можно получить двумя способами:

1. из уравнений описывающих процесс;

2. из соображения теории размерности.