Разложение вектора по базисным векторам.

Пусть заданапрямоуг. с-ма координат. Введем в рассмотрение единичные векторы, коорд. осей . -базисные вектора с-мы координат или орты. -произвольный вектор пр-ва. Отложим из начала координат вектор . По св-вам координат . Пусть числу на оси Ох соотв-ет точка , на . Тогда , ,

- ф-ла разложения по базисным векторам.

Пр. (1;2;3)

(1;0;0)+2(0;1;0)+3(0;0;1)=

Скалярное произведение векторов.

О.Скалярное произведение двух векторов и – число, равное произведению их модулей на угла между ними.

Св-ва:

ü

ü

ü тогда и только тогда, когда

ü угла между векторами вычисляется по ф-ле:

ü

ü

Т. Если векторы имеют координаты ; , тогда

Док-во:

Разложим исходные вертора по базисным векторам:а=a1*i+a2*j+a3*k;b=b1*i+b2*j+b3*k,перемножим

a*b=(a1*i+a2*j+a3*k)*( b1*i+b2*j+b3*k)={i*i=1,i*j=j*i=0,j*k=0,j*j=1,k*k=1}=

следствие:

1)cosf= /корень(а1^2+a2^2+a3^2)*(b1^2+b2^2+b3^2)

2)верторы ортогональны тогда и только тогда,когда =0

Правые и левые с-мы координат.

Три некомпланарных вектора в указанном порядке наз-ют тройкой векторов.

Пусть отложены из одной точки, будем смотреть из конца вектора на плоскость, содержащую и . Если кратчайший поворот от к осуществляется против часовой стрелки, то тройка векторов наз-тсяправой тройкой, если по часовой-то левой.

Векторное произведение векторов.

О. Векторным произведением на наз-тся , к-рый удовлетворяет след.условиям:

1.

2. каждому из векторов и

3.тройка векторов ,является правой

Св-ва:

ü

ü и -коллинеарны только тогда, когда =0

ü площадь параллелограмма, построенного на векторах и = модулю векторного произведения

ü

ü

ü

Т. Пусть , , тогда

Разложим и по базисным векторам

=

x	i	j	k
i
j
k

Пр.

тогда Смешанное произведение

О. Пусть даны 3 вектора . Умножим векторно, а полученный р-т скалярно на . В р-те получим число , называемое смешанным произведением векторов .

Смешанное произведение 3-х некомпланарных векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «+», если тройка правая и со знаком «-» - если левая.

Док-во:

Рассмотрим паралнлогрампостроенный на этих векторах.

16)Функции нескольких переменных.

Рассм. арифметическое -мерное пр-во ú

Пусть подмнож-во множ-ва . –нек-рое множ-во элементов , если каждому элементу ставится в соотв-е единственный элемент , то говорят, что на множ-ве задана ф-я

О. Пусть имеется переменных величин и каждому значению из некоторогомнож-ва соотв-ет одно, вполне определенное значение переменной . Тогда говорят, что задана ф-я нескольких переменных .

Ф-ла задает объем цилиндра, как ф-ю двух переменных . переменные величины называют независимыми переменными или аргументами. –зависимая переменная. Символ обозначает з-н соотв-я, множ-во 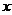– область определения.

Рассм. нек-рые примеры ф-и нескольких переменных. Ф-я 1) , -называется линейной; 2) -квадратичная ф-я.

Предел.

Множ-во точек , координаты к-рых удовлетворяют нер-ву <dназ-сяd -окрестностью точки .

О. Пусть нек-рая ф-я определена в нек-рой окрестности точки кроме самой точки . Число А наз-тся пределом ф-и при , или . Если для любого существует , такое что для всех и из -окрестности точки вып-тсянер-во <e.

, <e

Предел ф-и двух переменных обладает св-вами, аналогичнымисв-вам предела ф-и одной переменной. О.Ф-я наз-тсянепрерывной в точке если:

1.она определена в

2.имеет конечный предел при ,

3.этот предел = значению ф-и, т.е. .