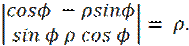Определение двойного интеграла по прямоугольной и произвольной областях.

Пусть D квадрируемое подмножество пространства R2, имеющее площадь S. Разбиением множества D ⊂ Rⁿ будем называть конечную совокупность τ={D1,...,Dk} непересекающихся множеств Di ⊂ D, таких, что

k

U Di = D. Диаметром разбиения τ называется число δ = max δ_i

i=1 i

δi—диаметр множества Di.

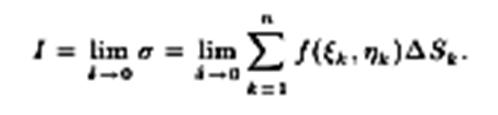
Пусть D ⊂ R², τ = {D1,...,Dk} — разбиение множества D, δ — диаметр разбиения τ, (ξi,ηi) — промежуточная точка множества Di, ∆Si — площадь Di. Функция f(x,y), определенная на D, называется интегрируемой на D, если существует конечный предел интегральных сумм

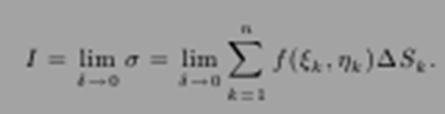
При этом сам предел I называют двойным интегралом (коротко — интегралом) от f на D и обозначают

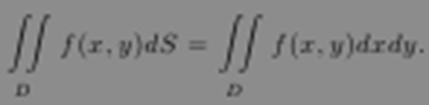
Ограниченность функции на D является необходимым условием интегрируемости.

Свойства двойного интеграла.

Линейность.

Теорема 9.1. Если fи g — интегрируемые функции, то линейная комбинация αf + βg также интегрируема и

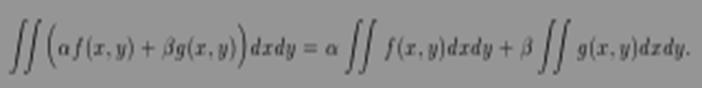
Монотонность.

Теорема 9.2. Если функции fи g интегрируемы на D и f(x,y) ﳰ g(x,y), ∀(x,y) ∈ D, то

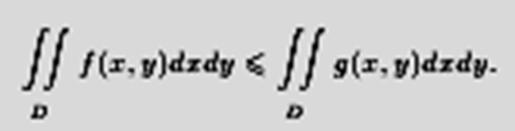
Аддитивность.

Теорема9.3.Пустьмножество D разбито на две частиD1 иD2,не имеющие общих внутренних точек. Если f интегрируема на D1 и на D2, то f интегрируема на D. Обратно, если f интегрируема на D, то на интегрируема также на D1 и на D2. При этом

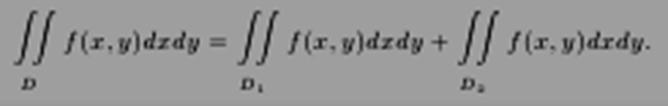
Теорема 9.4. Если f непрерывна на компакте D, то ∃(u,v) ∈ D такая, что

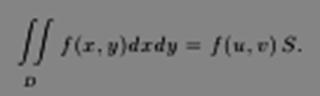
Сведение двойного интеграла к повторному

Рассмотрим функцию f(x,y), интегрируемую в квадрируемой области D.

Теорема 9.5. Пусть D —прямоугольник [a,b]х[c,d], и при ∀x ∈ [a,b] существует

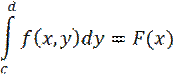
Тогда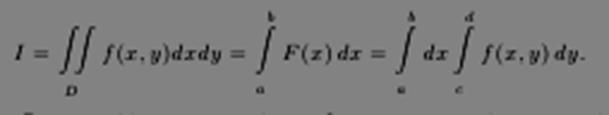

Множество D ⊂ R² называется выпуклым вдоль оси 0y, если любой отрезок, параллельный Oy, концы которого принадлежат D, целиком лежит в D. Это равносильно тому, что пересечение любой прямой, параллельная Oy, с границей множества D либо является отрезком, либо содержит не более двух точек.

Область D ⊂ R² , ограниченную прямыми x = a, x = b, (a<b), снизу кривой y = y1(x), сверху кривой y = y2(x) будем называть криволинейной трапецией.

Теорема 9.6. Пусть D ⊂ Rⁿ — криволинейная трапеция, ограниченная прямыми x = a, x = b, (a < b), снизу кривой y=y1(x), сверху кривой y = y2(x) Если при ∀x ∈ [a, b] существует

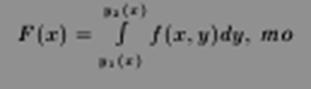
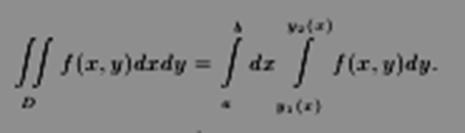
32. Преобразование фигуры и замена переменной в двойном интеграле. Использование полярных координат.

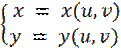(u, v) ∈ ∆

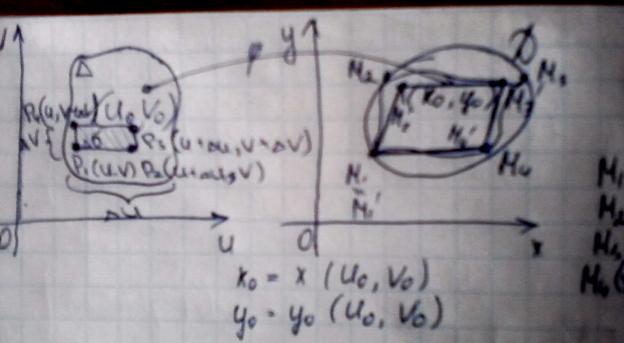
Вершины которого имеют координаты P1(u,v), P2(u + ∆u,v), P3(u + ∆u, v + ∆v), P4(u,v + ∆v).

Функции отображают прямоугольник P1P2P3P4 на некоторый криволинейный четырехугольник M1M2M3M4

M1(x(u, v), y(u, v)),

M2(x(u + ∆u,v),y(u + ∆u,v)),

M3(x(u + ∆u,v + ∆v),y(u + ∆u,v + ∆v)),

M4(x(u,v + ∆v),y(u,v + ∆v)).

Так как проекции отрезков M1’M2' и M3'M4' на оси координат равны, то M1'M2'M3'M4’– параллелограмм, площадь которого ∆s равна модулю определителя ∆

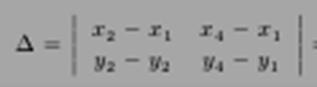
x=x(u,v,s) ∆=J(u,v)∆u∆v - якобиан

y=y(u,v,s) ∆s=|J(u,v)| ∆σ

z=z(u,v,s)

Замена переменных.

Пусть на компакте D ⊂ Rⁿ задана непрерывная функция f(x,y) и пусть функции

имеющие непрерывные производные по u и v, взаимно однозначно отображают компакт ∆⊂R² на компакт D⊂R². Тогда

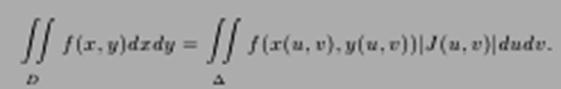
Связь между декартовыми координатами (x,y) точки и ее полярными координатами (ρ,ϕ) задается формулами

При замене переменных в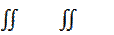

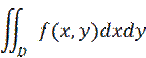
якобиан J(ρ, ϕ)=