График функции распределения

График функции распределения расположен в полосе, ограниченной прямыми у=0, у=1 . При возрастании хв интервале (а, b), в котором за­ключены все возможные значения случайной величины, график «поднимается вверх». При х£ а ординаты графика равны нулю; при х³ b ординаты графика равны единице.

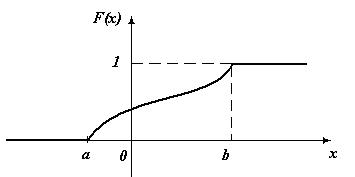
Рис. 8.1

Следует отметить, что график дискретной функции распределения имеет ступенчатый вид.

Плотность распределения вероятностей.
дифференциальная функция распределения

Плотностью распределения вероятностей непрерывной случайной величины Х называется функцию f(x) – первую производную от функции распределения: .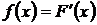

Для описания дискретной случайной величины плотность распределения неприменима. Иногда функцию плотности распределения называют дифференциальной функцией распределения. Линию y=f(x) называют кривой распределения.

Свойства плотности распределения

Свойство 1. Вероятность того, что непрерывная случайная величина в результате испытания примет какое-нибудь значение из интервала (a, b), равна определенному интегралу от плотности вероятности в пределах от aдо b:

.

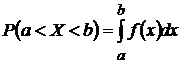Свойство 2. Если значения случайной величины принадлежат всей числовой оси, то имеет место утверждение .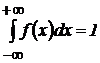

Свойство 3. Плотность вероятности функция неотрицательнаяf(x)³0.

Характеристики непрерывных случайных величин

Пусть непрерывная случайная величина Х задана плотностью распределения f(x) на отрезке [a, b].

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a, b], называется определенный интеграл:

.

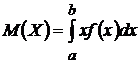Введем понятие дисперсии для непрерывной случайной величины, заданной

Дисперсией непрерывной случайной величины X называется математическое ожидание квадрата отклонений, если возможные значения принадлежат отрезку [a, b]:

.

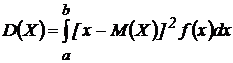Замечание. Для вычисления дисперсии непрерывной случайной величины удобно пользоваться формулой: .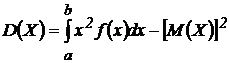

Среднее квадратическое отклонение непрерывной случайной величины определяется также как и для дискретной случайной величины:

.

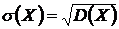Нормальное распределение

Нормальным называется распределение вероятностей случайной величины, которое описывается плотностью

.

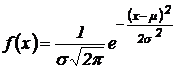Нормальное распределение определяется двумя параметрами m и s, m – математическое ожидание, s – среднее квадратическое отклонение.

График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Функция f(x) определена на всей оси х, при всех значениях х нормальная кривая расположена над осью Ох. Ось Ох служит горизонтальной асимптотой графика (рис. 8.2.); при 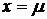функция имеет максимум, равный .

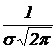Влияние параметров нормального распределения на
форму нормальной кривой

Изменение величины параметра m (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если m возрастает, и влево, если m убывает.

Если изменяется параметр s (среднее квадратическое отклонение). Так как максимум дифференциальной функции нормального распределения равен .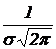

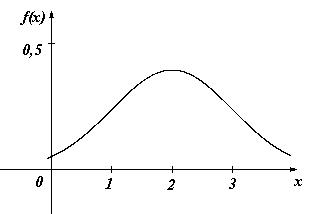
Рис. 8.2. Кривая Гаусса при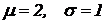

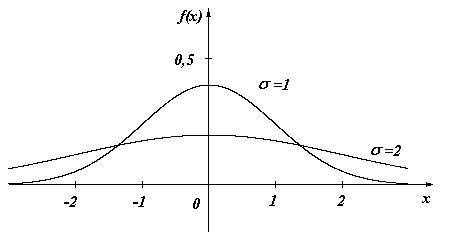
Рис. 8.3

Отсюда следует, чтос возрастанием s максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т. е. сжимается к оси Ох; при убывании s нормальная кривая становится более островершинной и растягивается в положительном направлении оси Оу (рис.8.3). Подчеркнем, что при любых значениях параметров m и s площадь, ограниченная нормальной кривой и осью х, остается равной единице.

Вероятность попадания в заданный интервал
нормальной случайной величины

Если случайная величина Х задана функцией плотности распределения вероятностей, то вероятность того, что в результате испытания Х примет какое-нибудь значение из интервала (a, b), равна определенному интегралу от плотности вероятности в пределах от a до b, то .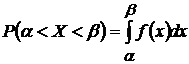

Если случайная величина распределена по нормальному закону, то можно доказать, что .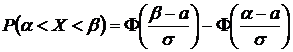

Решение задач

Пример 8.1. Дискретная случайная величина Х задана таблицей распределения

Х	1	4	8
Р	0,3	0,1	0,6

Найти функцию распределения и построить ее график.

Решение. Если х£.1 то F(x)=0 (третье свойство).

Если 1 < х £ 4, то F(х) = 0,3. Действительно, Х может принять значение 1 с вероятностью 0,3.

Если 4 < х £8, то F(х) = 0,4. Действительно, если х₁ удовлетворяет неравенству 4 < х₁£.8, то F(х₁) равно вероятности события Х < х₁, которое может быть осуществлено, когда Х примет значение 1 (вероятность этого события равна 0,3) или значение 4 (вероятность этого события равна 0,1). Поскольку эти два события несовместны, то по теореме сложения вероятность события Х < х₁ равна сумме вероятностей 0,3+0,1 =0,4.

Если х > 8, то F(x)=1. Действительно, событие Х<8 достоверно, следовательно, его вероятность равна единице.

Итак, функция распределения аналитически может быть записана так:

Сделаем рисунок:

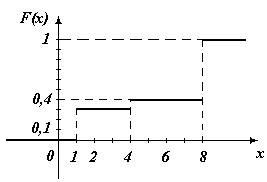
Пример 8.2. Случайная величина Х задана функцией распределения:

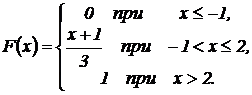
Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (0, 1).

Решение: так как на интервале (0, 1) функция распределения 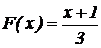, то на основании следствия 1 из свойства 2 имеем: Р(а£Х<b)=F(b)– F(a).

.

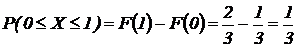Пример 8.3. Задана плотность вероятности случайной величины Х

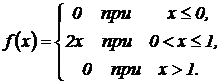
Найти вероятность того, что в результате испытания Х примет значение, принадлежащие интервалу (0,5; 1).

Решение: на основании свойства функции плотности вероятности 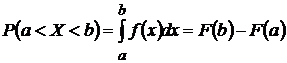имеем:

.

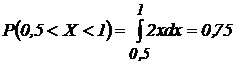Пример 8.4. Найти математическое ожидание и дисперсию непрерывной случайной величины, если 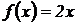на отрезке [0, 1].

Решение. Найдем математическое ожидание по формуле: ;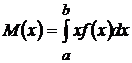

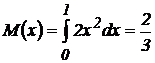. Найдем дисперсию по формуле: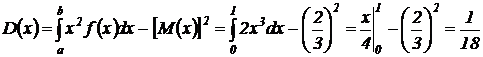

Пример 8.5. Нормально распределенная случайная величина Х задана дифференциальной функцией 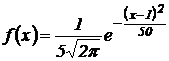. Найти математическое ожидание и дисперсию Х.

Ответ. М(Х)=1; D(Х)=25.

Пример 8.6. Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10, 50)

Решение. Если случайная величина распределена по нормальному закону, то 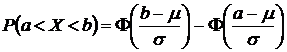, где Ф(х) – функция Лапласа (приложение 3).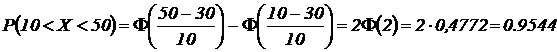

Самостоятельная работа студентов на занятии

1. Случайная величина Х задана функцией распределения. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (2, 3).

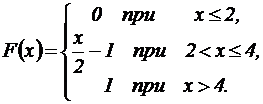
2. Задана плотность вероятности случайной величины Х

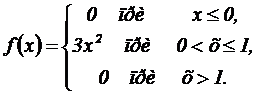
Найти вероятность того, что в результате испытания Х примет значение, принадлежащие интервалу ( ; 1).

3. Найти математическое ожидание и дисперсию непрерывной случайной величины a) на отрезке [0, 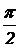], если 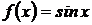; б) на отрезке [0, 1], если .

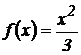4. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 10 и 2. Найти вероятность того, что в результате испытания Х примет значение в интервале (12, 14).

5. Автомат штампует детали. Контролируемая длина детали – случайная величина Х, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм и средним квадратическим отклонением σ=3 мм. Фактическая длина изготовленных деталей не мерее 32 мм и не более 68 мм. Найти вероятность того, что длина взятой детали: а) больше 55 мм; б) меньше 40 мм.

6. Написать дифференциальную функцию нормально распределенной случайной величины Х, зная, что М(Х)=3, D(Х)=16.

7. В компьютерном классе средствами Excel построить функцию плотности распределения, полученную в задаче 6.

Задание на дом

Практика

1. Случайная величина Х задана функцией распределения:

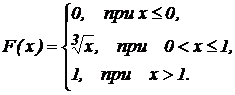
1) Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (0, 1).

2) Найти функцию плотности распределения вероятностей.

2. Случайная величина Х задана функцией распределения.

Найти функцию плотности распределения вероятностей.

3. Найти характеристики распределения для непрерывной случайной величины на интервале [0, 2], если .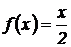

4. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найти вероятность того, что в результате испытания Х примет значение в интервале (15, 25).

5. Известно, что для человека pН крови является случайной величиной, имеющей нормальное распределение с математическим ожиданием 7,4 и средним квадратическим отклонением 0,2. Найти вероятность того, что уровень рН находится между 7,35 и 7,45 соответственно.

Теория

1. Лекция по теме «Задачи математической статистики. Генеральная и выборочная совокупности. Точечные оценки параметров распределения. Доверительный интервал и доверительная вероятность».

2. Занятие 9 данного методического пособия.

3. Павлушков И.В. и другие стр. 269-283.