Физический (механический) смысл производной

Скорость материальной точки в данный момент времени равна производной пути по времени

V = S't = dS/dt

(тока V с закорючками, ну типа скорость)

Производная суммы, произведения, степени, частного.

§ Производная от суммы или разности конечного числа ф-ции равна сумме или разности производных от этой ф-ции

§ (U+V+W)' = U'+V'-W'

§ Производная произведения двух ф-ций вычесл. по формуле (U*V)' = U'*V+V'*U

§ Производная частного

§ (U/V)'= U'V-V'U/V²

Производная сложной функции

Y'x=Y'u*U'x

Производная показательной и логарифмической ф-ции

логарифмическая ф-ция

(log a x)' = 1/x ln a

(ln x)' = 1/x

показательная фц-ия

( a в степени х)' = a в степени х*ln a

(E в степени х)' = е в степени х

Производные тригонометрических ф-ций

1)

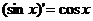
2)

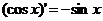
3)

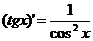
4)

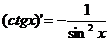
Производные обратных тригонометрических ф-ций

1)

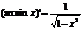
2)

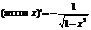
3)

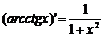
4)

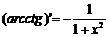
Возрастание,убывание ф-ций.Исследование ф-ции на монотонность по I пр-ной

Возрастание и убывание функция y = f (x) называется возрастающей на отрезке [a, b], если для любой пары точек х и х', а ≤ х < х' ≤ b выполняется неравенство f (x) ≤ f (x'), и строго возрастающей — если выполняется неравенство f (x) < f (x'). Аналогично определяется убывание и строгое убывание функции. Например, функция у = х² строго возрастает на отрезке [0,1], а

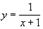строго убывает на этом отрезке. Возрастающие функции обозначаются f (x)↑, а убывающие f (x)↓. Для того чтобы дифференцируемая функция f (x) была возрастающей на отрезке [а, b], необходимо и достаточно, чтобы её производная f'(x) была неотрицательной на [а, b].

Наряду с возрастанием и убыванием функции на отрезке рассматривают возрастание и убывание функции в точке. Функция у = f (x) называется возрастающей в точке x₀, если найдётся такой интервал (α, β), содержащий точку x₀, что для любой точки х из (α, β), х> x₀, выполняется неравенство f (x₀) ≤ f (x), и для любой точки х из (α, β), х< x₀, выполняется неравенство f (x) ≤ f (x₀). Аналогично определяется строгое возрастание функции в точке x₀. Если f'(x₀) > 0, то функция f (x) строго возрастает в точке x₀. Если f (x) возрастает в каждой точке интервала (a, b), то она возрастает на этом интервале.

Экстремумы ф-ции.Исследование ф-ции на экстремум по первой производной.

Точка Х1 наз точкой максимума данной ф-ции, если выполняется условие

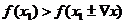
(рисунок)

Точка 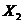наз минимумом данной ф-ции, если выполняется условие

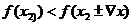
(рисунок)

Точки max и min наз. Экстремумом ф-ции

Теорема «необходимое условие существования экстремума»

Если ф-ция y=f(x) имеет в точке 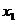экстремум и производная в этой точке существует,то обязательно выполняется условие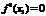

Геометрический смысл

(рисунок)

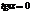
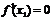
Вывод:любая экстремальная точка явл. критической,но не любая критич. точка будет экстремальной

План исследования ф-ции на экстремумы по 1-ой производной

1.находим D(y)

2.находим производную данной ф-ции

3.приравниваем полученную производную к 0 и вычесляем критические точки.

4.полученными точками разбиваем область опред. на интервалы и опред. знак производной в каждом интервале

5.если при переходе через критическую точку слева еаправо,производная меняет знак с +на-,то данная точка-max ф-ции,если с –на+, то точка- min ф-ции

6. находим значение ф-ции в экстремальных точках путем их подстановки в условие.